自动搬运

查看原文

来自洛谷，原作者为

	bmatrix ⁧⁧‭

搬运于2025-08-24 22:43:10，当前版本为作者最后更新于2022-11-22 10:22:58，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题面

初步分析

由于题目有大样例，观察样例发现，答案只能是 $2,3,4$ 之一。如果你不相信肉眼观察法也没有关系，容易证明，任何答案不为 $2$ 或 $3$ 的情况都可以通过以下方法构造出答案为 $4$ 的方案：

1. 寻找两条竖直线 $l_1,l_2$，记 $l_1$ 左侧的点数为 $a$，右侧点数为 $b$，$l_2$ 左侧点数为 $c$，右侧点数为 $d$，使得 $a<b,c>d$ 且 $b-a,c-d$ 的值分别最小。
2. 显然两条直线之间必然有且只有一列点，且一定能找到一条水平线（记这列点中在水平线上面的点数为 $e$，下面的点数为 $f$）使得 $a+e=d+f$。

求解

显然答案为 $2$ 的情况，就是存在一条平行于坐标轴的直线能恰好将所有点平均分为两份。（两个折点分别从在 $(0,0)$ 折出去时和折到 $(10^{100},10^{100})$ 时出现）

如图所示：

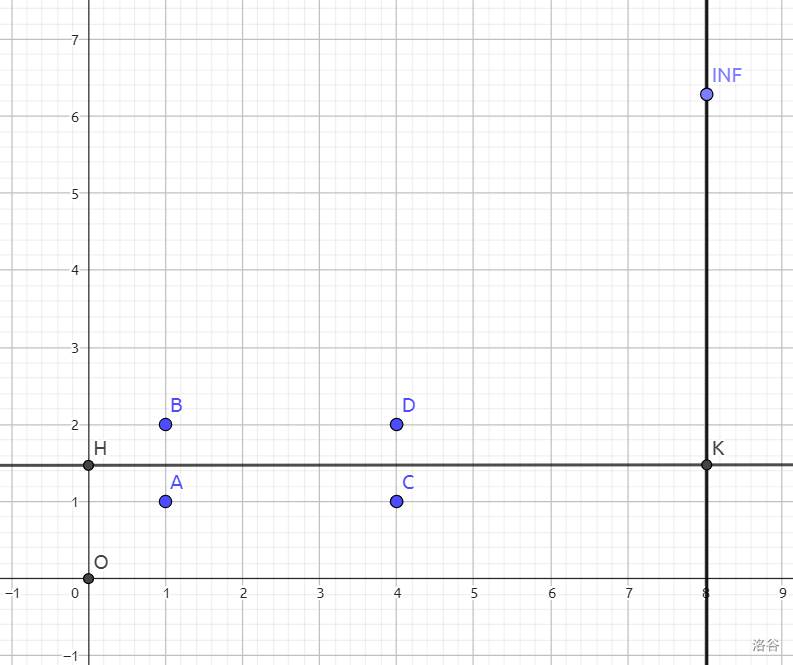
由于这条直线可能横也可能竖，所以我们只需要把所有点分别按横 / 纵坐标排序，然后看中间两个点的横 / 纵坐标是否相等，不相等就说明答案为 $2$，否则不是。

对于答案为 $3$ 的情况，我们发现它就是在给定的点之间的某个地方多转了一次，分为两种情况：

1. 从原点出发后往右走，然后往上走，再往右走
2. 从原点出发后往上走，然后往右走，再往上走

容易发现第一种走法切割出了右下角的一块矩形区域，而第二种走法切割出了左上角的一块矩形区域，只要这个矩形区域所包含的点数等于 $\dfrac n2$，就说明答案为 $3$。

样例 2，往右走的情况：

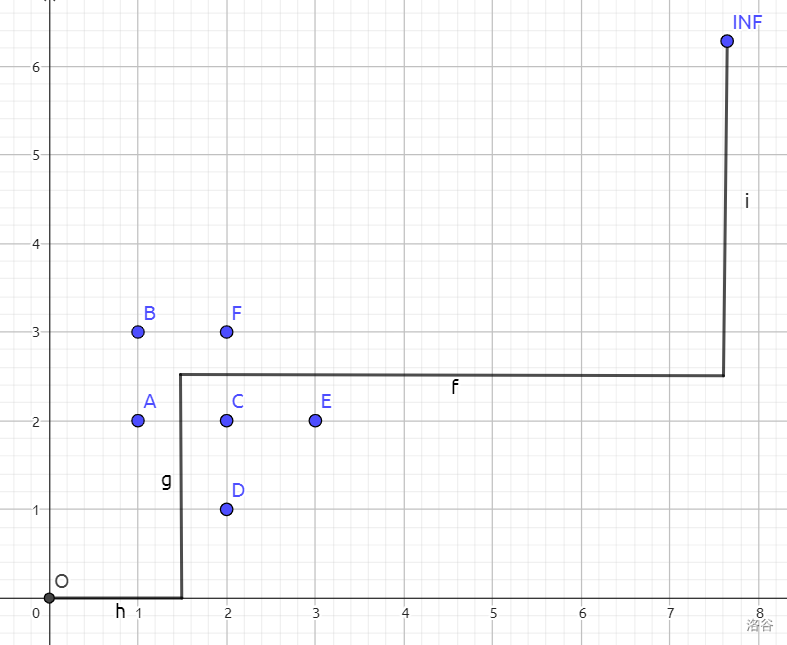
接下来考虑如何判断是否存在这样的矩形。

由于两种情况同理，考虑其中一种即可，如果要求右下角的那种，先将点按横坐标排序，从右往左遍历在哪两列点之间向上走，用树状数组记录纵坐标，二分往右转的位置判断能否恰为 $\dfrac n2$ 个点即可。

对于答案为 $4$ 的情况，排除即可：如果答案既不是 $2$ 也不是 $3$，那就是 $4$ 了。

时间复杂度 $O(n\log^2n)$，常数挺小的。

#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s; i <= e; ++i)
#define per(i, s, e) for(int i = s; i >= e; --i)
#define F first
#define S second
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef __int128_t i128;
typedef __uint128_t u128;
typedef pair<int, int> pii;
constexpr int N = 5e5 + 5;
int tr[N], n, t;
#define lb(x) ((x) & (-(x)))
void add(int i, int v) {
    for(; i <= n; i += lb(i)) tr[i] += v;
}
int sum(int i) {
    int res = 0;
    for(; i; i -= lb(i)) res += tr[i];
    return res;
}
void clear() {
    rep(i, 1, n) tr[i] = 0;
}
void solve() {
    cin >> n;
    vector<pii> a;
    rep(i, 1, n) {
        int x, y; cin >> x >> y;
        a.emplace_back(x, y);
    }
    sort(a.begin(), a.end(), [](pii a, pii b){return a.S == b.S ? a.F < b.F : a.S < b.S;});
    if(a[n / 2].S != a[n / 2 - 1].S) {
        cout << 2 << endl; return;
    }
    sort(a.begin(), a.end());
    if(a[n / 2].F != a[n / 2 - 1].F) {
        cout << 2 << endl; return;
    }
    int i = 0;
    while(i < n) { // 寻找左上角的矩形
        int t = a[i].F;
        while(i < n && a[i].F == t){
            add(a[i].S, 1);
            ++i;
        }
        if(i < n / 2) continue;
        int l = 1, r = n;
        while(l < r) {
            int mid = (l + r) / 2;
            int s = i - sum(mid);
            if(s == n / 2) {
                cout << 3 << endl; return;
            }
            if(s < n / 2) r = mid;
            else l = mid + 1;
        }
    }
    clear(); // 别忘了清空
    i = n - 1;
    while(i >= 0) { // 寻找右下角的矩形
        int t = a[i].F;
        while(i >= 0 && a[i].F == t){
            add(a[i].S, 1);
            --i;
        }
        if(i > n / 2) continue;
        int l = 1, r = n;
        while(l < r) {
            int mid = (l + r) / 2;
            int s = sum(mid);
            if(s == n / 2) {
                cout << 3 << endl; return;
            }
            if(s < n / 2) l = mid + 1;
            else r = mid;
        }
    }
    cout << 4 << endl;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    cin >> t;
    while(t--) solve(), clear();
    return 0;
}