自动搬运

查看原文

来自洛谷，原作者为

	__K2FeO4 Purple, Indigo, Lavender, Lilac, Grape, Ningyezi, Amethyst, Hyacinth, Mauve, Blurple

搬运于2025-08-24 22:43:04，当前版本为作者最后更新于2022-11-19 13:38:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

我们分类讨论。

设 $p$ 为 $1$ 的个数，$q$ 为 $-1$ 的个数。

Part 1: $p\le q$

容易发现最小的最大子段和为 $1$，这也就意味着两个 $1$ 之间一定有至少一个 $-1$（不然最大子段和大于 $1$ 了）。

这样，就是在 $q$ 个 $-1$ 之间（包括两端）插入 $p$ 个“隔板”$1$，方案总数为 $C_{q+1}^{p}$。

Part 2: $p>q$

在这种情况下，最大子段和为 $p-q$。我们画图分析。

$1$ 表示向右上方走 $1$ 个对角线单位，$-1$ 表示向右下方走 $1$ 个对角线单位。对于任意时刻保持 $0\le y\le p-q$ 的路径方案数。

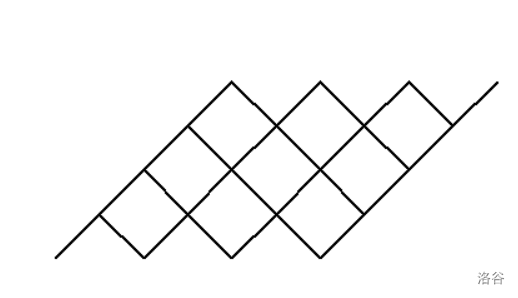
就是如图从左下角到右上角的方案数。

设 $f{i,j}$ 为使用 $i$ 个 $-1$，前缀和为 $j$ 的方案数（使用 $i$ 个 $-1$ 就是如图从左上开始的层数，前缀和为 $j$ 就是当前高度），得到状态转移方程：

$f_{i,j}=f_{i-1,j+1}+f_{i,j-1}$

初始化 $f_{0,0}=1$。

答案为 $f_{q,p-q}$。

code:

注意空间复杂度，可以选择用 vector，也可以用滚动数组（这个更好）。

#include<bits/stdc++.h>
using namespace std;
const int N=10086;
const int mod=998244353;
typedef long long ll;
int n,cp=0,cq=0;
vector<int> a[N];
signed main(){
	int x;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	scanf("%d",&x),x==1?cp++:cq++;
	int m=cp-cq;
	//a[0].push_back(1);
	if(m>0){
		for(int i=0;i<=cq;i++)
		for(int j=0;j<=m;j++){
			int s=0;
			if(i&&j!=m)s+=a[i-1][j+1];
			if(j)s+=a[i][j-1];
			a[i].push_back(i||j?s%mod:1);
			//printf("%d ",i||j?s%mod:1);
		}
		printf("%d",a[cq][m]);
	}
	else{
		for(int i=0;i<=1-m;i++)
		for(int j=0;j<=cp;j++){
			int s=0;
			if(i)s+=a[i-1][j];
			if(j)s+=a[i][j-1];
			a[i].push_back(i||j?s%mod:1);
		}
		printf("%d",a[1-m][cp]);
	}
	return 0;
}