自动搬运

查看原文

来自洛谷，原作者为

	Graphcity 循此苦旅，终抵繁星。

搬运于2025-08-24 22:42:49，当前版本为作者最后更新于2022-11-06 09:34:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

2024.2.19 Update：更新了剪贴板中的代码链接。

---

下文中默认 $n,q$ 同阶。在考场上，显然要先从好做的部分分开始想。

• $k=1$ 时，答案就是路径上的点权之和，树链剖分 / 倍增维护即可，时间复杂度 $O(n\log n)$。（16pts）

• $n\le 200$ 时，考虑转化为图论模型。若两个点 $a,b$ 满足 $dis(a,b)\le k$，则连一条连接 $a,b$ 的双向边。那么答案即为从 $s$ 到 $t$ 的点权和最短的路径。时间复杂度 $O(n^3\log n)$，菊花图可以卡满。（20pts）

接下来要做的事就是深入挖掘题目中的性质。

根据直觉可以意识到，除了路径上的点，最优方案中其它经过的点距离这条路径至少不会很深。

先作出大胆的猜想：最优方案中只会经过路径上的点。

• $k=2$ 时，这确实是合法的。为什么呢？如果你从路径上的点跳到某个点的儿子再跳回路径，显然不如直接跨过这个点。

  

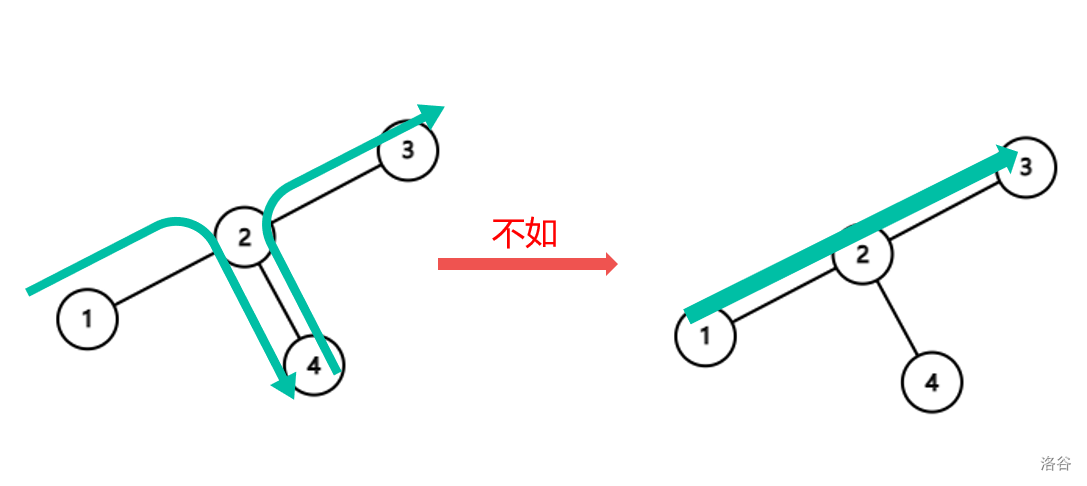
  把路径提取出来，考虑用 DP 来表示。设 $f_i$ 为跳到第 $i$ 个点的最小值，可以得到 $f_i=\min(f_{i-1},f_{i-2})+val_i$。（20pts）

• 但 $k=3$ 时这东西就有点问题，因为你可以从一个儿子跳到另一个儿子，而且这正有可能是最优的方案。

  经过一些小修正，我们可以发现，当 $k=3$ 时，最优方案中只可能存在路径上的点和他们的一个儿子。我们这里把 LCA 的父亲结点也当作它的儿子之一。

  

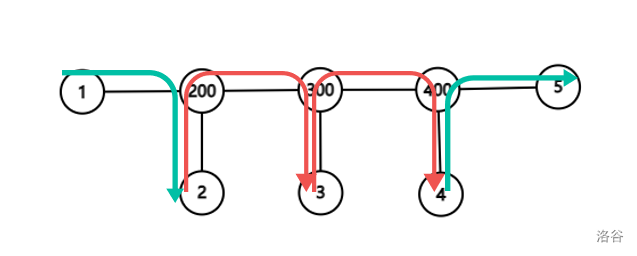
  显然这个儿子需要满足不在路径上，而且它的权值也要最小。事实上，它要么是最大值，要么是次大值。把路径提取出来后，我们可以方便的 $O(1)$ 把这玩意求出来。设 $num_i$ 表示 $i$ 儿子的权值，如果没有则设为 $\infty$。

  设 $f_{i,0/1}$ 表示跳到了点 $i$ 自己 / 它儿子的最小值，枚举它从哪个点跳过来，可以得到

$$\begin{aligned} f_{i,0}&=\min(f_{i-1,0},f_{i-1,1},f_{i-2,0},f_{i-2,1},f_{i-3,0})+val_i\\ f_{i,1}&=\min \begin{cases} f_{i,0}+num_i \\ \min(f_{i-1,0},f_{i-1,1},f_{i-2,0})+num_i \end{cases} \end{aligned} $$

这两个部分的时间复杂度均为 $O(nd)$，其中 $d$ 为树的深度。（20pts）

至此，你已经得到了 76pts 的好成绩。（76pts 考场代码）

再往下就是解决 $n\le 2\times 10^5$ 的正解情况了。对于部分分，它的时间复杂度瓶颈在于一次 $O(d)$ 的动态规划。我们必须着手去优化它。

这个时候，你想到了 NOIP2018 保卫王国，这道题也需要优化树上 DP 的过程。

尝试借鉴它的思路，考虑 动态 DP。下文中对矩阵乘法 $A\times B=C$ 的定义如下，它满足结合律：

$$C_{i,j}=\min_{k}(A_{i,k}+B_{k,j})$$

• 对于 $k=1$ 的情况，转移矩阵非常好处理，甚至根本不需要转移矩阵。这里为了与下文统一，用的是 $3\times 3$ 的矩阵。

$$\begin{bmatrix} val_i & \infty & \infty \\ \infty & 0 & \infty \\ \infty & \infty & 0 \end{bmatrix} \begin{bmatrix} dis_{i-1}\\ 0\\ 0 \end{bmatrix} = \begin{bmatrix} dis_{i}\\ 0\\ 0 \end{bmatrix} $$

• 对于 $k=2$ 的情况，它的状态转移方程 $f_i=\min(f_{i-1},f_{i-2})+val_i$ 也容易写成矩阵形式：（12pts）

$$\begin{bmatrix} val_i & val_i & \infty \\ 0 & \infty & \infty \\ \infty & \infty & 0 \end{bmatrix} \begin{bmatrix} f_{i-1}\\ f_{i-2}\\ 0 \end{bmatrix} = \begin{bmatrix} f_{i}\\ f_{i-1}\\ 0 \end{bmatrix} $$

• 但是，当 $k=3$ 时，我们需要存 $f_{i,0},f_{i,1},f_{i-1,0},f_{i-1,1},f_{i-2,0}$ 这五个值，一次转移就有 $5^3=125$ 的常数，即使是 3s 的时限也难以接受。这个时候就必须要优化状态设计。

  可以发现，整个 DP 中影响转移的只有一个因素——距离。设 $f_{i,0/1/2}$ 表示跳到距离点 $i$ 为 0/1/2 的点的最小值，则有：

$$\begin{aligned} f_{i,0}&=\min(f_{i-1,0},f_{i-1,1},f_{i-1,2})+val_i\\ f_{i,1}&=\min \begin{cases} f_{i,0}+num_i\\ \min(f_{i-1,0},f_{i-1,1})+num_i\\ f_{i-1,0} \end{cases} \\ f_{i,2}&= f_{i-1,1} \end{aligned} $$

把中间的 $f_{i,0}$ 拆开，再把式子整理一下，可以得到：

$$\begin{aligned} f_{i,0}&=\min(f_{i-1,0},f_{i-1,1},f_{i-1,2})+val_i\\ f_{i,1}&=\min(f_{i-1,0},f_{i-1,1}+num_i,f_{i-1,2}+val_i+num_i)\\ f_{i,2}&= f_{i-1,1} \end{aligned} $$

接下来给出 $k=3$ 的转移矩阵：

$$\begin{bmatrix} val_i & val_i &val_i \\ 0 & num_i & num_i+val_i \\ \infty & 0 & \infty \end{bmatrix} \times \begin{bmatrix} f_{i-1,0}\\ f_{i-1,1}\\ f_{i-1,2} \end{bmatrix} = \begin{bmatrix} f_{i,0}\\ f_{i,1}\\ f_{i,2} \end{bmatrix} $$

我们把路径上第 $i$ 个点的转移矩阵称为 $base_i$。根据动态 DP 的套路，设路径长度为 $k$，整个转移过程如下：

$$\begin{aligned} \begin{bmatrix}f_{k,0}\\f_{k,1}\\f_{k,2} \end{bmatrix}&=base_k\times \begin{bmatrix}f_{k-1,0}\\f_{k-1,1}\\f_{k-1,2} \end{bmatrix}\\ &=base_k\times base_{k-1}\times \begin{bmatrix}f_{k-2,0}\\f_{k-2,1}\\f_{k-2,2} \end{bmatrix}\\ &\ \ \vdots\\ &=base_{k}\times base_{k-1}\times \cdots \times base_2\times \begin{bmatrix}f_{1,0}\\f_{1,1}\\f_{1,2} \end{bmatrix}\\ \end{aligned} $$

答案就是除开第一个点外的转移矩阵逆序积再乘上初始的转移矩阵。

利用倍增预处理出从点 $i$ 往上跳 $2^k$ 级祖先之和的矩阵顺序乘积和逆序乘积，询问就可以直接解决了。

等等...是不是有点问题？

对于每条路径，$num_i$ 的值有可能不同。如何保证 $num_i$ 不在路径上？

通过观察，可以发现，$num_i$ 的意义实际上就是给一个结点挂一个值为 $num_i$ 的儿子。如果 $num_i$ 在路径上，那么 最优方案一定不会经过 $i$ 的任何一个儿子。因为对于走到 $i$ 儿子的方案，要么一定不优，要么可以把儿子替换成 $num_i$，方案合法的同时答案仍然不劣。

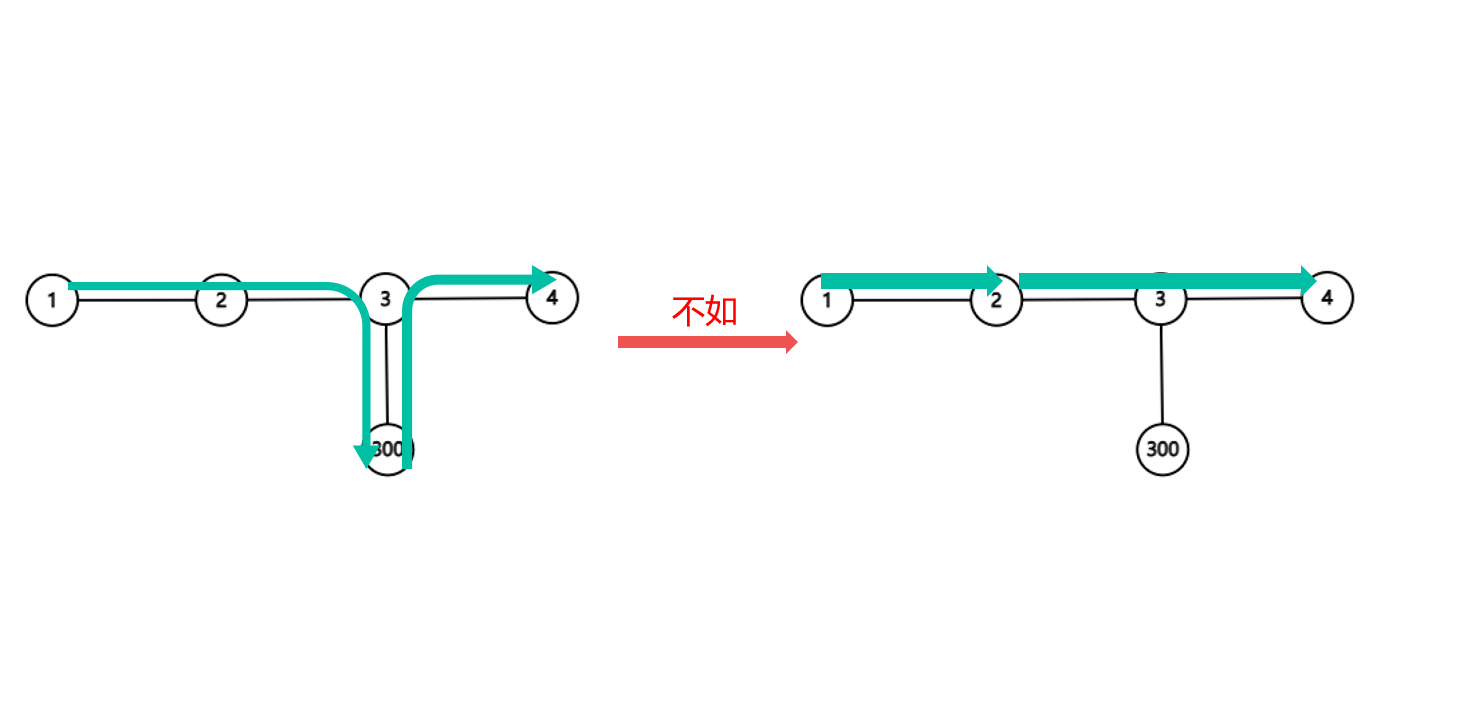
所以直接预处理出 $num_i$ 为 $i$ 直接连接的结点中权值最小值即可。

这种方法的分类讨论和细节都是较少的。时间复杂度 $O(n\log n)$。（12pts）

现在，你已经成功的切掉了这道题。（AC Code）