自动搬运

查看原文

来自洛谷，原作者为

	SkyWave RetroVision

搬运于2025-08-24 22:42:45，当前版本为作者最后更新于2022-11-07 21:52:11，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

本题解亮点：不用建表达式树或者用栈

这道题没有那么难，大家都想复杂了

思路

分治/伪表达式树

vp 完的那个夜晚，大家讨论做法时都一致认定这道题在考表达式树，于是我就看了看他们发的代码。清一色的要么是建表达式树，最后跑一遍遍历，要么是用一个栈弹来弹去，还有厉害的则先将中缀表达式转成前/后缀表达式，然后再求值。

我还是太弱了，看着大佬们一百多行的代码陷入了沉思。

我的评价是：太抽象了！有没有一种方法既不用建表达式树，不用栈弹来弹去，也不用转成前/后缀表达式，实现直接在中缀表达式求值呢？

我们可以先来思考一下人类是怎么算中缀表达式的：

就先拿样例 1 举例：

0&(1|0)|(1|1|1&0)

人类会先看向第一层的 | 左边的 0&(1|0)，再看向 & 左边的 0，此时形成了一个短路，所以这部分的值为 0。

此时式子为 0|(1|1|1&0)。

此时 | 左边的值计算完毕，我们该看 第一层的 | 右边的 (1|1|1&0)。

此时我们会先看到 1|1|1&0，发现第二层的 | 左边为 1，构成短路，此部分的值为 1，后面的操作都不用算。

此时式子变为 0|(1|1&0)

我们会看到 (1|1&0)，发现又构成一次短路，此部分的值为 1。

此时式子会变成 0|1，最后算出答案为 1。

为什么要分析的那么仔细？因为我们等会就要实现通过模拟人脑计算中缀表达式的过程计算中缀表达式。

我们先来分析一下我们做的过程。我们会先找到第一层优先级最高的，先算这个符号的左半边，判断存不存在短路，如果不存在，继续找找到第二层优先级最高的，算这个符号的左半边，判断存不存在短路……以此类推。当不存在比他优先级更高的时候，计算这一层的值并将当前算式替换成这部分的值继续求解。

对于刚才样例的人脑操作，流程图如下。

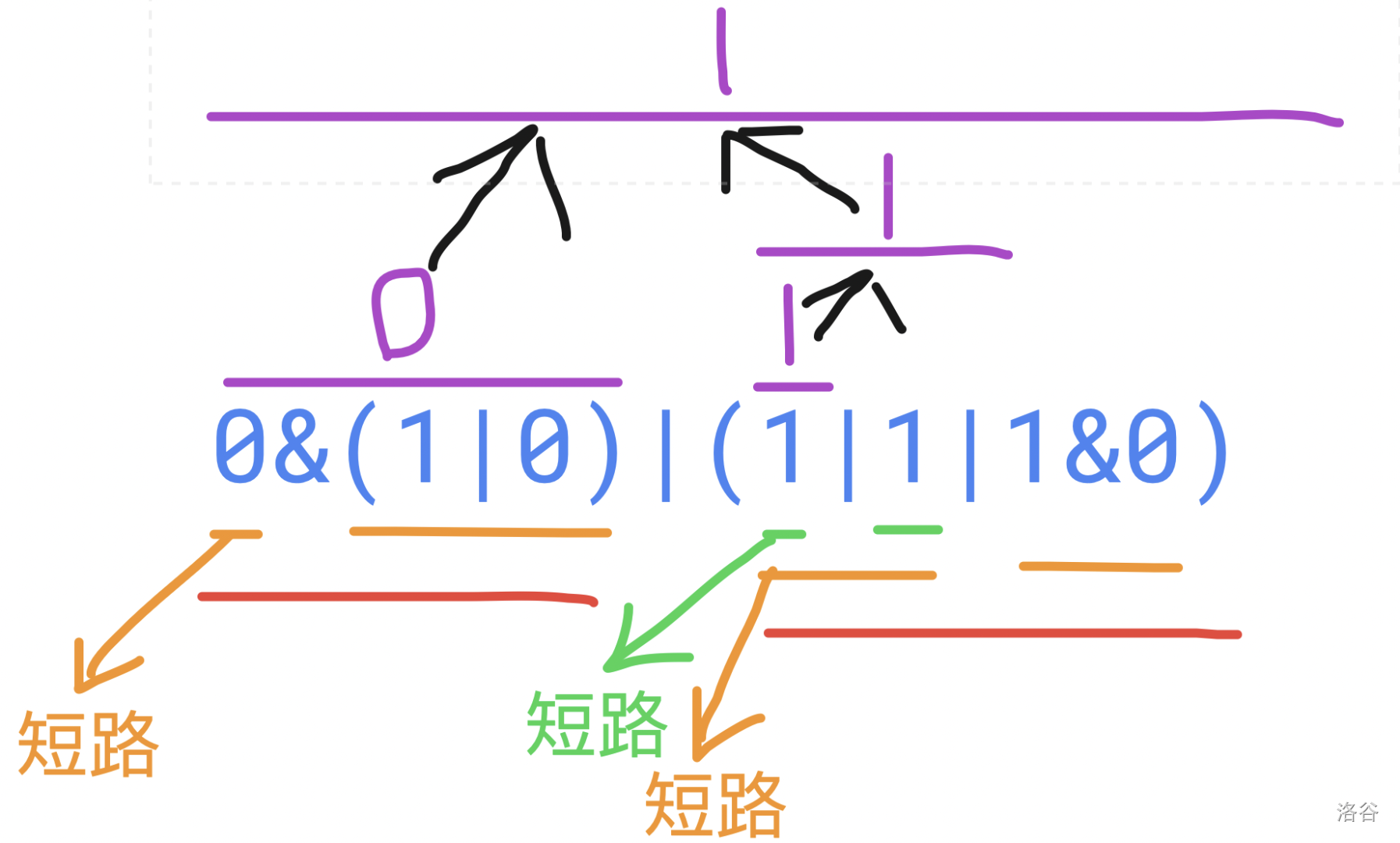
我们会先找到第一层优先级最高的，也就是第一层的 | 左半边，然后我们进入左半边，找这个左半边里优先级最高的，自然是第二层的 &。看他的左半边，是一个 0，造成了短路，所以这一部分的值就是 0。然后我们回到第一层，第一层的左半边我们算完了，值为 0，但因为第一层是 |，所以不造成短路。我们继续找 ｜ 号的右半边优先级最高的，发现是第二层的 | ，于是我们再去左半边找优先级最高的运算符，此时我们会找到第三层的 |，看他的左半边。发现没有运算符，只有一个数字，为 1！并且他右边的运算符为 |，构成一个短路，于是这部分的值就是 1。第三层算完了，我们回到第二层，发现是一个 |，并且我们刚才的计算结果为 1，于是又构成一次短路。此时回到第一层，我们只需要计算出 0|1 的结果就行，答案为 1。

我们来回顾一下刚才的过程。我们每次都会重复寻找当前层优先级最高的符号，并先到符号左边继续寻找当前层优先级最高的符号……直到当前层没有符号，即只有数字为止，此时我们当前层的结果就是这个数字，返回到上一层。此时我们通过刚才计算的结果和这一层的符号判断是否存在短路，如果没有短路就计算出符号右边的值后再计算在这一层的值，并回到上层。否则我们不用计算右边的值，直接回到上一层利用已算出的值继续计算……

把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并，这个算法叫什么？

对了！分治。

那我们该怎么分解问题呢？

我们每次会找到这一层不在括号里的最后一个运算级最低的运算符，然后递归到他的左半边和右半边分别求解，这一层的值就等于左半边的值和右半边的值做这个运算符的操作。（如果是 | 那么就是左半边的值 | 右半边的值，& 同理。

那问题来了，我们不是优先级高的先算吗？为什么要“找到这一层不在括号里的最后一个运算级最低的运算符”呢？

好问题！恰恰因为先找，所以才后算。递归是用类似于栈的先进后出机制，我们每次把运算级最低的先进栈，最后回溯的时候反而运算级最低的在最底下了。此时我们回溯就会先从运算级最高的开始算并返回到上一层了。大家可以在纸上画个表达式，自己玩一玩。

那如果这一层没有“不在括号里的最后一个运算级最低的运算符”怎么办？那就要分两种情况了。一种情况是整个算式都被括号包起来了，此时我们把括号去掉就行了。还有一种是只有数字，此时我们只要返回这个数字就行了，也就是我们分治的边界条件。

那我为什么要叫它伪表达式树呢？

来看这张图：

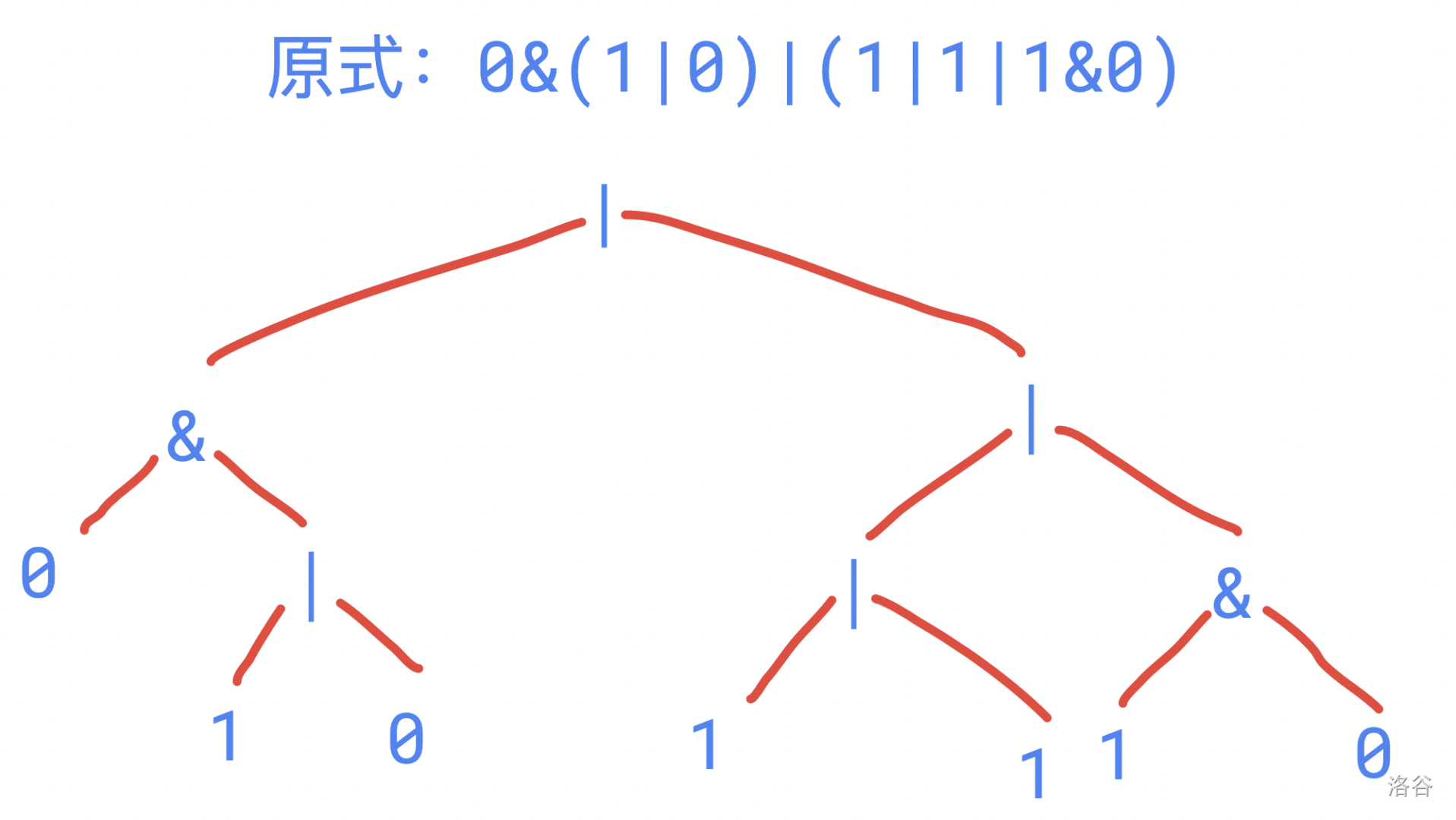
通过中缀表达式树的建立也可以用上面的代码实现——找到最后一个在括号外的符号，让他作为根节点，符号的左边就是他的左子树，右边就是他的右子树。但有没有必要把它存下来再遍历呢？多此一举！因为我们在遍历的时候就相当于在通过计算机能理解的顺序访问这棵树了，可以边访问边计算。

思路部分完结撒花！

代码

边上代码边讲！

//
//  main.cpp
//  P8815 [CSP-J2022] 逻辑表达式（暂无数据）
//
//  Created by SkyWave Sun on 2022/10/29.
//

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define N (int)1e6 + 1
char str[N];
int sum1;
int sum2;
int dfs(int l,int r) {
    int x = 0,orpos = 0, andpos = 0;//记录括号层数、最后一个 | 出现的位置、最后一个 & 出现的位置
    for (int i = l; i<=r; ++i) {//遍历左右区间查找运算符
        if (str[i] == '(') {
            ++x;//增加一层括号
        }else {
            if (str[i] == ')') {
                --x;//减少一层括号
            }else {
                if (!x) {//不在括号中
                    if (str[i] == '|') {
                        orpos = i;
                    }else {
                        if (str[i] == '&') {
                            andpos = i;
                        }
                    }
                }
            }
        }
    }
    if (orpos) {//注意，因为 | 比 &优先级低，要先判断存不存在 |
        if (str[orpos] == '|') {
            int tmp1 = dfs(l, orpos - 1);//遍历左区间
            if (tmp1 == 1) {//如果是 1，触发了 | 短路
                ++sum1;
                return 1;//不需要计算右区间，直接返回 1
            }else {
                int tmp2 = dfs(orpos + 1, r);//计算右区间
                return (tmp1 | tmp2);
            }
        }
    }
    if (andpos) {
        if (str[andpos] == '&') {
            int tmp1 = dfs(l, andpos - 1);
            if (tmp1 == 0) {//如果是 0，触发了 & 短路
                ++sum2;
                return 0;//不需要计算右区间，直接返回 0
            }else {
                int tmp2 = dfs(andpos + 1, r);
                return (tmp1 & tmp2);
            }
        }
    }
    //不在括号内的运算符不存在
    if (str[l] == '(' && str[r] == ')') {//如果都被括号包裹着
        return dfs(l + 1, r - 1);//去掉括号
    }else {
        return str[l] - '0';//否则左右区间一定重合，返回数字就行了
    }
}
int main(int argc, const char * argv[]) {
    scanf("%s",str + 1);
    int len = strlen(str + 1);
    int sum = dfs(1, len);
    printf("%d\n%d %d\n",sum, sum2, sum1);//注意！一定要开个 sum 把dfs结果先记下来，否则直接输出会导致 UB
    return 0;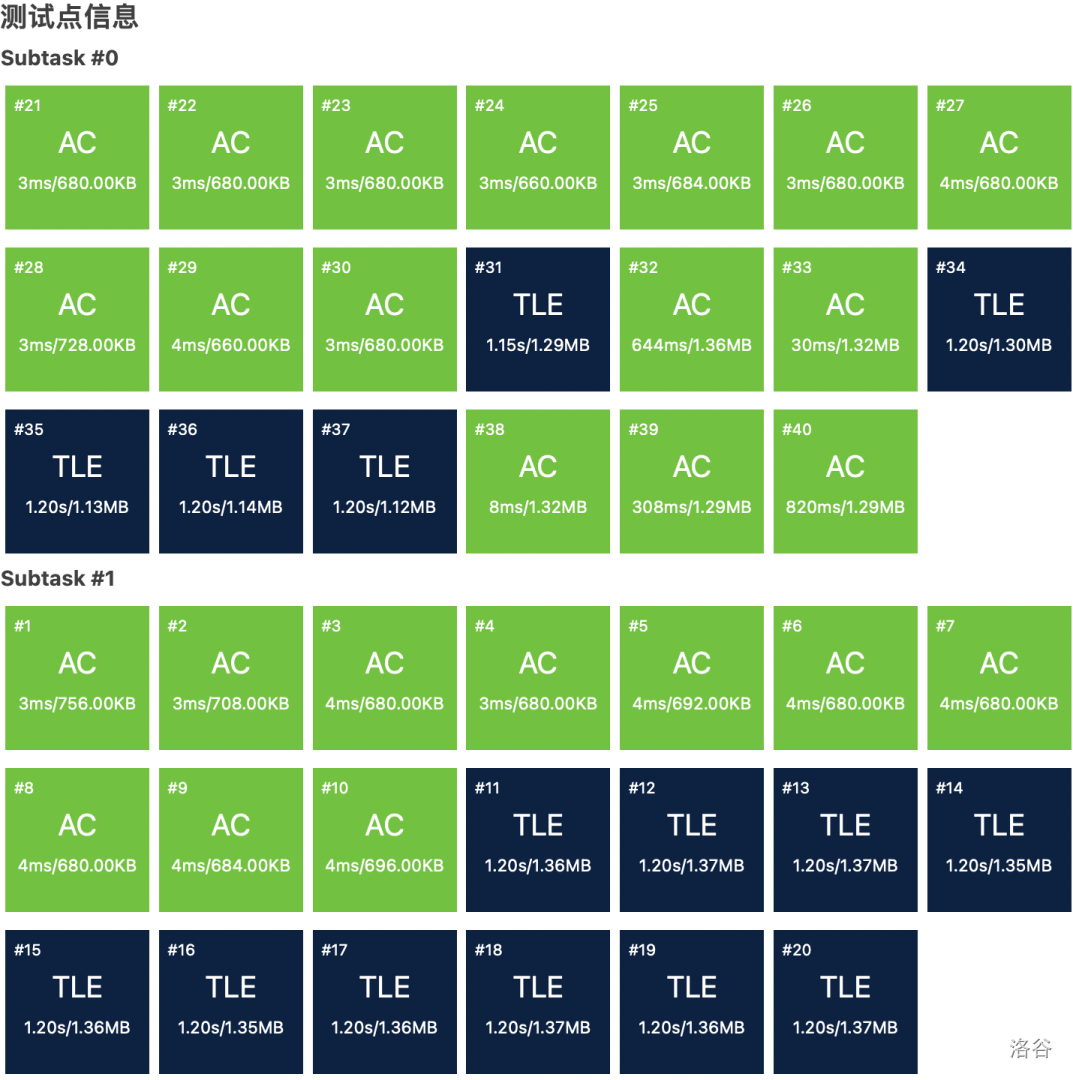
}

为什么会这样呢？

原因很简单——刚才的程序时间复杂度为 $O(n^2)$。因为我们在每次分治求解的时候都遍历一遍字符串，时间效率太低。如果我们能预处理出来字符串，那时间复杂度将降低为 $O(n)$。

那我们怎么预处理呢？好办，我们对每个位置，处理出这个位置左侧和它同层的最后一个（离它最近的）运算符。这样一来，我们在递归时，想看这一层的最后一个运算符，也就只需访问与右边界同层的最后一个运算符就行了，省掉了每次都遍历一遍的过程。注意，别忘了判断一下这个运算符的位置是否在左边界的右边，否则就说明这一层没有运算符。

依然是结合代码讲解。

优化版：

//
//  main.cpp
//  P8815 [CSP-J 2022] 逻辑表达式（民间数据）
//
//  Created by SkyWave Sun on 2022/11/3.
//

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define N (int)1e6 + 1
char str[N];
int c1[N];
int c2[N];
int l1[N];
int l2[N];
int cnt1;
int cnt2;
int dfs(int l,int r) {//记得先看主函数的预处理
    if (c1[r] >= l) {//如果最后一个和 r 同层的 ｜ 在 l 和 r 的范围内
        int ans = dfs(l, c1[r] - 1);
        if (ans == 1) {
            ++cnt1;
            return 1;
        }
        return (ans | dfs(c1[r] + 1, r));
    }
    if (c2[r] >= l) {//如果最后一个和 r 同层的 & 在 l 和 r 的范围内
        int ans = dfs(l, c2[r] - 1);
        if (ans == 0) {
            ++cnt2;
            return 0;
        }
        return (ans & dfs(c2[r] + 1, r));
    }
    if (str[l] == '(' && str[r] == ')') {
        return dfs(l + 1, r - 1);
    }
    return str[l] - '0';
}
int main(int argc, const char * argv[]) {
    scanf("%s",str + 1);
    int len = strlen(str + 1);
    int x = 0;//括号层数
    //l1[x] 代表目前最后一个在 x 层括号的 ｜ 运算符
    //l2[x] 代表目前最后一个在 x 层括号的 & 运算符
    //c1[i] 代表目前和 i 同层的最后一个 | 运算符
    //c2[i] 代表目前和 i 同层的最后一个 & 运算符
    for (int i = 1; i<=len; ++i) {
        if (str[i] == '(') {
            ++x;
        }else if (str[i] == ')') {
            --x;
        }else if (str[i] == '|') {
            l1[x] = i;
        }else if (str[i] == '&') {
            l2[x] = i;
        }
        c1[i] = l1[x];//最后一个在 i 这个位置前且与 i 同层的 | 运算符
        c2[i] = l2[x];//最后一个在 i 这个位置前且与 i 同层的 & 运算符
    }
    int ans = dfs(1, len);
    printf("%d\n%d %d\n",ans,cnt2,cnt1);
    return 0;
}

一片绿色，蔚为壮观！

完结撒花！

我是 SkyWave，这是我的第四篇题解，有不足之处请多多指出，有任何看不懂的地方欢迎留言或者私信！