自动搬运

查看原文

来自洛谷，原作者为

	sgl654321 风起雨停，天又放晴

搬运于2025-08-24 22:42:26，当前版本为作者最后更新于2022-12-03 11:51:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目大意

给定一个 $n\times m$ 的矩阵，求其中有多少个子矩阵的所有元素之和小于等于 $k$。

解题思路

• $30$ 分做法：

要想确定一个矩阵，只需要确定其左上角的点 $(x1,y1)$ 和右下角 $(x2,y2)$ 的点即可。注意 $x1\le x2,y1\le y2$。

枚举左上角的点和右下角的点，再扫描 $x\in[x1,x2],y\in[y1,y2]$ 的所有点，暴力加起来，就得到了一个矩阵中的所有元素之和。与 $k$ 比较并统计答案。

时间复杂度 $O(n^3\times m^3)$。

• $70$ 分做法：

与 $30$ 分做法相同，扫描左上角与右下角的点，耗费 $O(n^2\times m^2)$ 的时间复杂度。考虑如何 $O(1)$ 求出矩阵中的元素之和。

使用二维前缀和，用 $sum[i][j]$ 表示矩阵中 $x\in[1,i],y\in[1,j]$ 的所有元素之和。其递推式为 $sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]$，具体不再赘述。

所以矩阵该矩阵的元素之和就可以用 $sum[x2][y2]-sum[x2-1][y1]-sum[x1-1][y2]+sum[x1-1][y1-1]$ 来表示。我们就做到了 $O(1)$ 求出矩阵中的元素之和。

时间复杂度 $O(n^2\times m^2)$

• 满分做法：

考虑如何把复杂度压到三次方的级别。

我们可以假想有水平的两条横线，切出了中间一块区域。用 $O(n^2)$ 的时间，枚举这两条横线（如下图所示）。

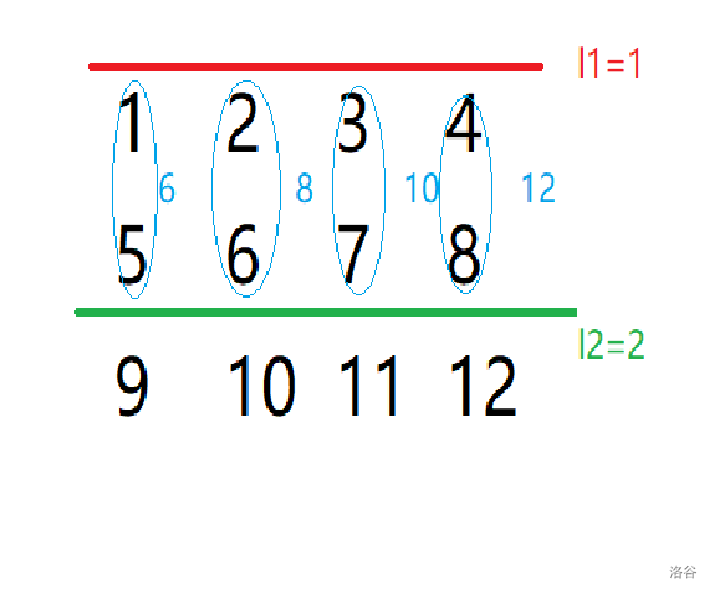
枚举出两条横线之后，就可以把中间的每一列数给当成一个整体，例如上图 $l1=1,l2=2$ 的情况下，就可以把矩阵视为一个序列 $[6,8,10,12]$。

我们只需要求出在这个序列中，有几个子序列的元素之和小于等于 $k$ 即可。这就把二维问题转化为了一维问题，这种“降维打击”的方法，是很多题目解题的切入点。

那么现在我们还有 $O(m)$ 的时间来处理子序列的问题。考虑有两个指针 $l$ 和 $r$，代表子序列的左端点与右端点。注意到矩阵中所有的元素都是正数，那么显然有下面两个结论：

1. 若 $sum(l,r)\le k$，且 $l+1\le r$，则 $sum(l+1,r)\le k$。
2. 若 $sum(l,r)>k$，且 $r+1\le n$，则$sum(l,r+1)>k$。

在遍历 $r$ 时，如果当前的子序列元素和小于等于 $k$，那么就有 $r-l+1$ 个新答案。如果大于 $k$ 了，就考虑向右移动 $l$，使得最终的子序列元素和仍然小于等于 $k$。

举个例子：有一个序列 $[1,3,4,3]$，试求出其中有多少个子序列，满足该子序列的所有元素之和小于等于 $10$。

• $l=1,r=1,sum=1,ans=0+(1-1+1)=1$
• $l=1,r=2,sum=4,ans=1+(2-1+1)=3$

批注：因为 $l=1,r=2$ 都可以，那么 $l=2,r=2$ 肯定可以。

• $l=1,r=3,sum=8,ans=3+(3-1+1)=6$
• $l=1,r=4,sum=11$

批注：此时考虑移动 $l$ 使得 $sum\le k$。 只需要向右移动一格 $l$ 就行了。

• $l=2,r=4,sum=10,ans=6+(4-2+1)=9$

此时 $r=4$，且有解了，停止循环。

参考代码与总结

#include<bits/stdc++.h>
using namespace std;
long long n,m,k,a[510][510],sum[510][510],b[510];
long long l,r,now,ans;
int main(){
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			cin>>a[i][j];
	for(int j=1;j<=m;j++)
		for(int i=1;i<=n;i++)
			sum[i][j]=sum[i-1][j]+a[i][j];
	for(int x=1;x<=n;x++)
		for(int y=x;y<=n;y++){
		//	cout<<x<<" "<<y<<":"<<endl;
			for(int j=1;j<=m;j++)
				b[j]=sum[y][j]-sum[x-1][j];
			//双指针
			l=1;r=1;now=0;
			for(r=1;r<=m;r++){
				now+=b[r];
				if(now<=k){
				//	cout<<l<<" "<<r<<" "<<now<<endl; 
					ans+=r-l+1;
				}
				else{
					while(now>k){
						now-=b[l];
						l++;
					}
					ans+=r-l+1;
				}
			}
		//	cout<<"-------"<<endl;
		}
	cout<<ans<<endl;
	return 0;
}

总结：该题的解题方法：

1. “降维打击” 法：把二维问题转化为一维。
2. 双指针法：把 $O(n^2)$ 的复杂度，通过单调性等优秀性质，转化为 $O(n)$。