自动搬运

查看原文

来自洛谷，原作者为

	lottle1212 **

搬运于2025-08-24 22:42:01，当前版本为作者最后更新于2023-06-30 22:19:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

原题链接

这是一道 贪心 + DP 好题，具有一定的思维难度。

题目大意

• 给出一棵 $N(N \leq 10 ^ 5)$ 个节点树，求出这棵树通过“左孩子右兄弟”表示法转化成的二叉树高度最大值。

解题思路

首先通过 贪心 大法，我们容易想到一棵树根据题意处理后的最大高度即根节点儿子数 + 儿子中的最大高度。样例如图：

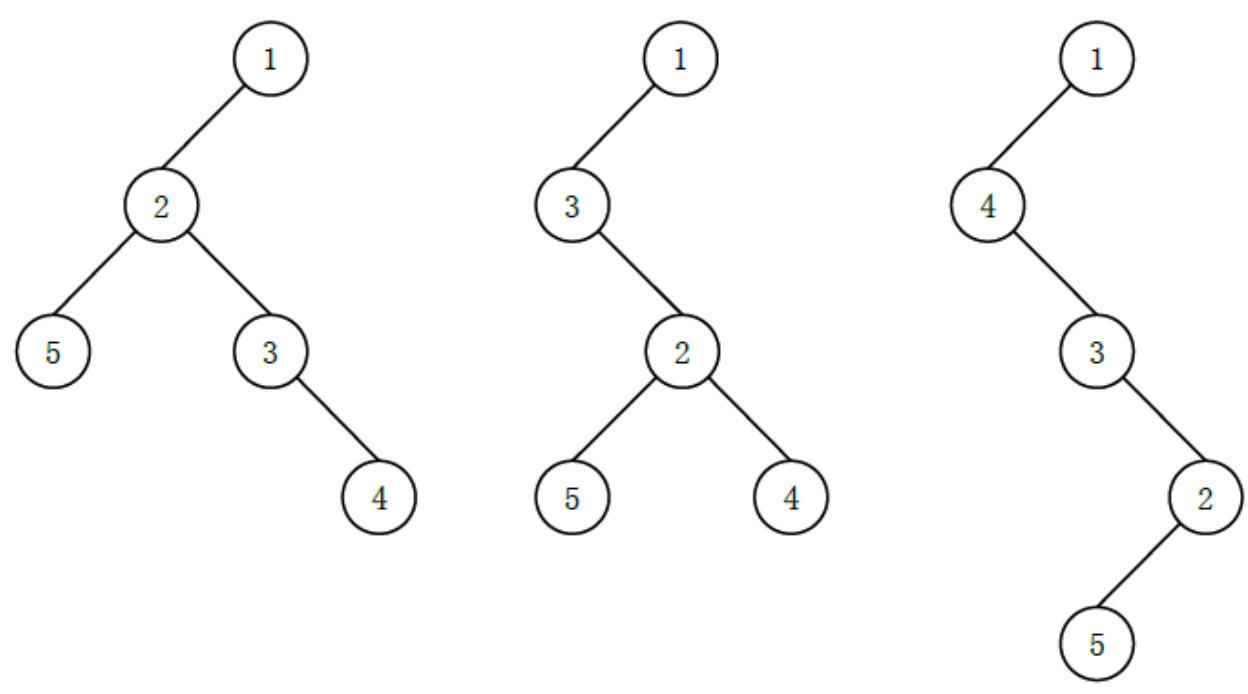
我们把根节点的儿子串在一条链上，最下方是高度最大的儿子，即得答案 $4$（根节点高度为 $0$）。

最后，用简单清晰的 树形 DP 进行转移就可以了。

AC Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 1e5 + 10; 
ll n, sz[N], head[N], dp[N], cnt, u;
struct Edge { ll nxt, to; } e[N << 1];
void add(ll u, ll v) { e[++ cnt] = {head[u], v}; head[u] = cnt; } //链式前向星
void dfs(ll u) {
	for(ll i = head[u], v; i; i = e[i].nxt) {
		v = e[i].to;
		dfs(v);
		dp[u] = max(dp[u], dp[v]);
	}
	dp[u] += sz[u];
} //树形 DP
signed main() {
	cin >> n;
	for(ll i = 2; i <= n; ++ i) cin >> u, add(u, i), ++ sz[u];
	dfs(1);
	cout << dp[1];
	return 0;
}