自动搬运

查看原文

来自洛谷，原作者为

	wuhan1234 **

搬运于2025-08-24 22:41:51，当前版本为作者最后更新于2023-04-08 12:13:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

A 合数个数

直接用循环进行枚举搜索。编写的函数如下。

void work1()
{
    int ans=0;
    for (int i=4;i<=2020;i++)
    {
        int j;
        for (j=2;j*j<=i;j++)
            if (i%j==0) break;
        if (j*j<=i) ans++;
    }
    printf("%d\n", ans);
}

执行上面的处理函数，输出结果为：$1713$。

B 含 $2$ 天数

直接用循环对每一天进行枚举判断，若年、月、日数字中含有 $2$，则计数。 编写的函数如下。

int check(int x)   // 判断整数x 中是否含有数字 2
{
	while(x)
    {
		if (x%10==2) return 1;
		x/=10;
	}
	return 0;
}
void work2()
{
    int month[2][13]={{0,31,28,31,30,31,30,31,31,30,31,30,31},
                      {0,31,29,31,30,31,30,31,31,30,31,30,31}};
    int y,m,d,ans=0;
    for (y=1900;y<=9999;y++)
    {
        int f;
        if (y%400==0||(y%4==0 && y%100!=0)) f=1;
	    else f=0;
    	for (m=1;m<=12;m++)
        {
    		for (d=1;d<=month[f][m];d++)
    		{
    			if (check(y)||check(m)||check(d)) ans++;
			}
		}
	}
    printf("%d\n", ans);
}

执行上面的处理函数，输出结果为：$1994240$。

C 本质上升序列

用线性动态规划进行求解。

定义状态 $dp_i$ 表示以字符 $s_i$ 结尾的本质不同的方案数。

由于第 $i$ 个字符的状态只会和前 $i-1$ 个字符有关，因此我们需要枚举前 $i-1$ 个字符。

当前 $i-1$ 个字符中有某个字符 $s_j$ 和 $s_i$ 相同时，那么就会出现重复的方案；但是由于 $dp_i$ 是一定已经包含了 $dp_j$ 的，所以为了避免重复，可以令 $dp_j=0$。

当前 $i-1$ 个字符中有某个字符 $s_j$ 小于 $s_i$ 时，那么 $dp_i=dp_i+dp_j$。因为 $s_i>s_j$，所以直接在以 $s_j$ 结尾的本质上升序列结尾加一个字符 $s_i$，这样也是一个本质上升序列。这样可以继承 $dp_j$ 的所有可行方案。

当前 $i-1$ 个字符中有某个字符 $s_j$ 大于 $s_i$ 时，直接跳过即可。

最后结果便是 $dp_1+dp_2+…+dp_{200}$。

编写的函数如下。

void work3()
{
    int dp[210]={0};
    char s[210]="tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhewl";
    int ans = 0;
    int i,j;
    for (i=0;i<strlen(s);i++)
    {
    	dp[i]=1;
    	for (j=0;j<i;j++)
    	{
    		if (s[i]==s[j]) dp[i]=0;
    		else if (s[j]<s[i]) dp[i]+=dp[j];
		}
	}
	for (i=0;i<strlen(s);i++)  ans+=dp[i];
    printf("%d\n", ans);
}

执行上面的处理函数，输出结果为：$3616159$。

D 咫尺天涯

一个 $k$ 阶的皮亚诺曲线有 $3^k$ 行，每行 $3^k$ 列，共 $3^k\times 3^k$ 个格子，在这些格子中，每行中相邻的格子数有 $3^k-1$ 个，每列中相邻的格子数也有 $3^k-1$ 个，因此相邻的格子总数为 $2\times 3^k \times (3^k-1)$ 个。

例如，$1$ 阶皮亚诺曲线中相邻的格子有 $2\times 3 \times (3-1)=12$ 个。

$2$ 阶皮亚诺曲线中相邻的格子有 $2\times 3^2 \times (3^2-1)=2\times 9 \times 8=144$ 个。

由题目给出的示意图可知，一个 $k$ 阶的皮亚诺曲线可以划分为 $9$ 个 $k-1$ 阶的皮亚诺曲线，而每个 $k-1$ 阶曲线内部相邻两个格子的距离和不受其余同阶曲线的影响。

设一个 $k-1$ 阶皮亚诺曲线内部相邻两个格子的距离和为 $a$，每两个 $k-1$ 阶皮亚诺曲线间上下相邻的格子的距离和为 $b$，每两个 $k-1$ 阶皮亚诺曲线间左右相邻的格子的距离和为 $c$，则一个 $k$ 阶皮亚诺曲线内部相邻两个格子的距离和为 $9\times a+b+c$。

例如，对于 $2$ 阶皮亚诺曲线中相邻的格子有 $144$ 个，若将 $2$ 阶皮亚诺曲线看成由 $9$ 个 $1$ 阶皮亚诺曲线组成，则每个 $1$ 阶皮亚诺曲线内部相邻的格子有 $12$ 个，两个 $1$ 阶皮亚诺曲线的水平方向上相邻的格子有两行，每行 $9$ 个格子，垂直方向上相邻的格子有两列，每列同样 $9$ 个格子。如下图所示。也就是 $2$ 阶皮亚诺曲线中相邻的 $144$ 个格子可以分解为 $9\times 12 +2\times 9 +2\times 9$。

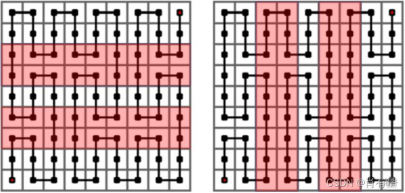
因此，可以从低阶的距离和递推计算出高阶的距离和。其中关键是求低阶曲线之间水平和垂直相邻的距离和 $b$ 和 $c$。

由图可发现，两行或两列之间相邻块的距离和是相等的，于是只需讨论一行或一列的距离和的计算方法，将其和乘以 $2$ 即可。 若将 $k$ 阶的皮亚诺曲线的最左下角的格子设置为原点 $(0,0)$，水平向右为 Y 轴，垂直向上为 X 轴，则每个格子的坐标就确定了。

$k$ 阶的皮亚诺曲线有 $3^k$ 行格子，$k-1$ 阶的皮亚诺曲线有 $3^{k-1}$ 行格子，因此水平方向上，$x$ 值为 $3^{k-1}$ 和 $3^{k-1}-1$ 的格子上下相邻，其 $y$ 值从 $0 \sim 3^k$。

对于相邻的两个格子 $(x,y)$ 和 $(x-1,y)$ 计算出它们与原点的距离，则差的绝对值就是相邻两个格子的距离。

求一个格子 $(x,y)$ 与原点 $(0,0)$ 之间的距离采用递归完成，可参看程序代码。

编写的函数如下。

long long p[14];
long long abs(long long a)
{
    return a > 0 ? a : -a;
}
long long calc(int k, long long x, long long  y) //求k阶曲线中(x,y)与原点（0.0)的距离
{
    if (k == 0) return 0;
    long long offset = x / p[k] * 3;
    int flag = (offset == 3);
    offset += flag ? (3 - y / p[k] - 1) : (y / p[k]);
    if ((offset & 1) == 1)
        x =  p[k] - x % p[k] - 1;
    if (flag )
         return  ((offset + 1) * p[k] * p[k] - calc(k - 1, x % p[k], y % p[k]) - 1) ;
    else
         return  (offset * p[k] * p[k] + calc(k - 1, x % p[k], y % p[k])) ;
}
void work4()
{
    int i,j;
    p[1]=1;
    for (i = 2; i <= 13; i++)
        p[i] = p[i-1] * 3;
    long long ans=0;
    for (i = 1; i <= 12; i++)
    {
        long long tmp = 0;
        for (j = 0; j < p[i + 1]; j++)
        {
            tmp += abs(calc(i, j, p[i]) - calc(i, j, p[i] - 1));
            tmp += abs(calc(i, p[i], j) - calc(i, p[i] - 1, j));
        }
        ans = 9 * ans + 2 * tmp;
    }
    printf("%lld", ans);
}

执行上面的处理函数，输出结果为：$184731576397539360$。

E 玩具蛇

从 $16$ 个方格中的每个方格作为起点，分别用 DFS 进行搜索，若从某个起点出发能走 $16$ 步，则就是一种可行的方案。

int dx[4]={1, -1, 0, 0};
int dy[4]={0, 0, 1, -1};
int ans=0;
int vis[16];
int len;
void dfs(int n)
{
    if (len == 16)
    {
        ans++;
        return;
    }
    for (int i = 0; i < 4; i++)
    {
        int nx = n / 4 + dx[i];
        int ny = n % 4 + dy[i];
        if (nx < 0 || nx >= 4 || ny < 0 || ny >= 4)
            continue;
        int next = 4 * nx + ny;
        if (!vis[next])
        {
            vis[next] = 1;
            len++;
            dfs(next);
            vis[next] = 0;
            len--;
        }
    }
}
void work5()
{
    for (int i = 0; i < 16; i++)
    {
        vis[i] = 1;
        len++;
        dfs(i);
        vis[i] = 0;
        len--;
    }
    printf("%d\n", ans);
}

执行上面的处理函数，输出结果为：$552$。

有了上面的处理结果，提交给本题的源程序如下。

#include <stdio.h>
#include <string.h>
int main()
{
    char T;
    scanf("%c",&T);
    if (T=='A') printf("1713\n");
    else if (T=='B') printf("1994240\n");
    else if (T=='C') printf("3616159\n");
    else if (T=='D') printf("184731576397539360\n");
    else if (T=='E') printf("552\n");    
    return 0;
}