自动搬运

查看原文

来自洛谷，原作者为

	liangbob 我们生活在大地上，但我们的梦想超越天空。

搬运于2025-08-24 22:41:46，当前版本为作者最后更新于2023-06-14 07:48:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P8720 题解

思路分析

小学几何题。

几何题没有图，我不是很满意。

我们先来证明一个结论：设平面在加入某不重合于已有线后与原已有线交点数为 $x$，则该平面会增加 $x + 1$ 个部分。

证明如下：

这个线产生 $x$ 个交点，我们把它单独拎出来看一下。

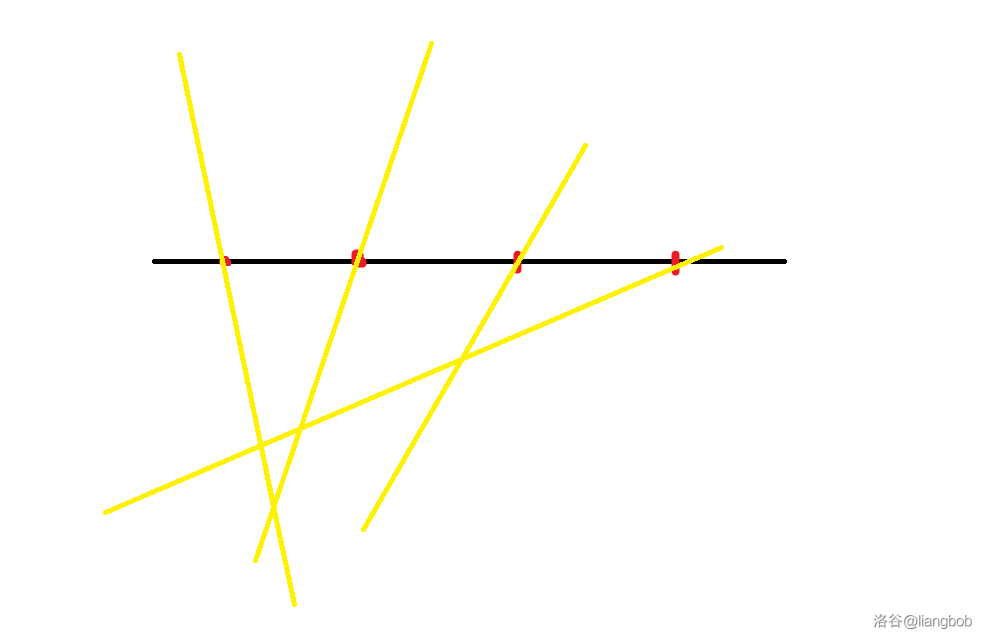
可以看到，黑线上被红色点截，会出现 $x + 1$ 段线段。

而这些线段，经过的刚好就是一个部分，刚好把这个部分从一个变成了两个，部份数加了一。

每条线段都一样，所以会增加 $x+1$ 个部分。

证毕。

接着，我们再来证明一个结论：

直线 $y=k_1x+b_1$ 与 $y = k_2x+b_2$ 的交点横坐标为 $\dfrac{b_2-b_1}{k_1-k_2}$，纵坐标为 $k_1 \cdot \dfrac{b_2-b_1}{k_1-k_2} +b_2$。

话不多说，先上图：

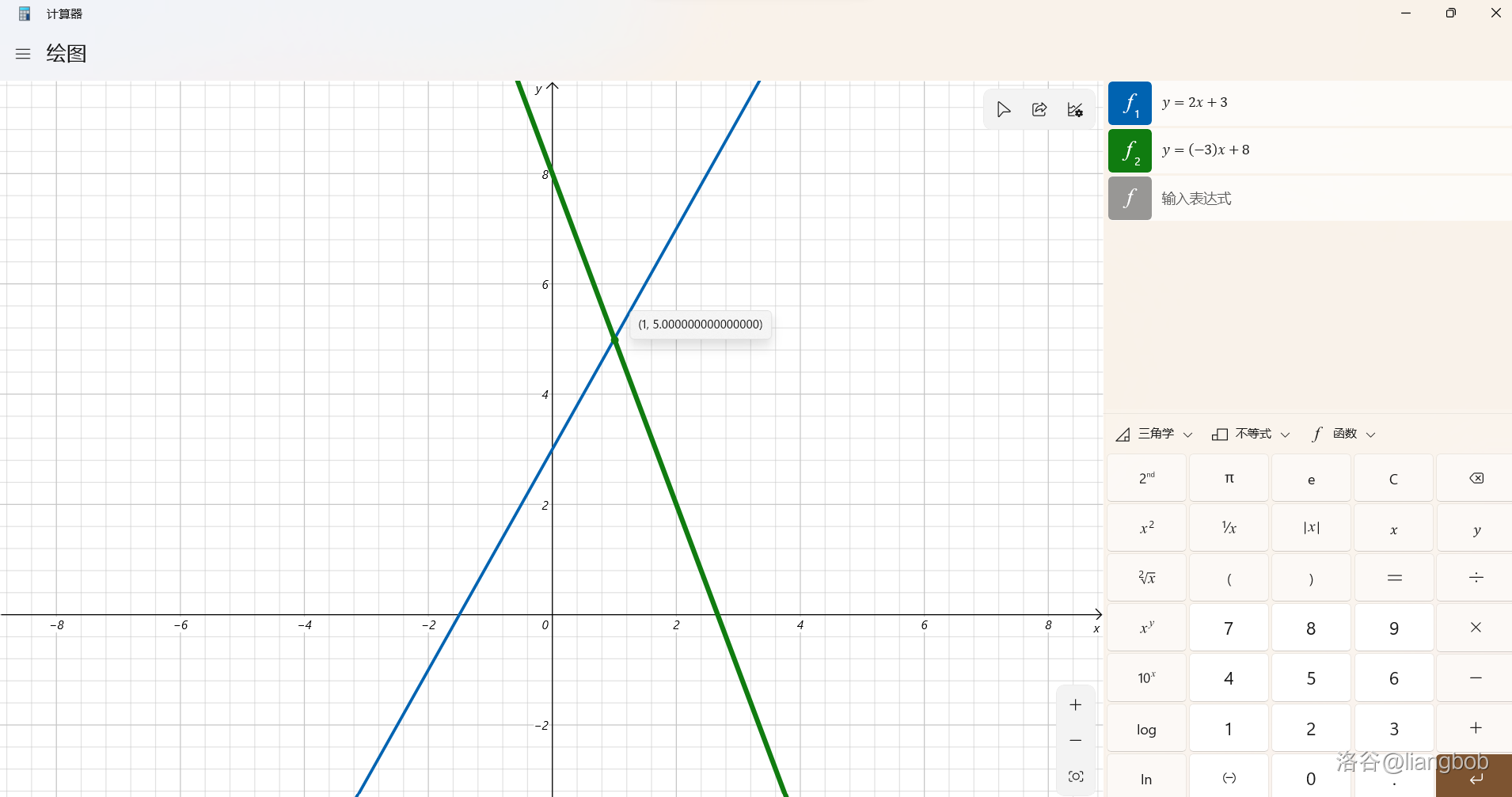
中间的小点就是交点。

可以看到，这个交点 $x$ 轴与 $y$ 轴是相同的。所以可以联立两个式子为方程组，得：

$$\begin{cases}y=k_1x+b_1\ldots\ldots①\\y = k_2x+b_2\ldots\ldots②\end{cases} $$

将 $② - ①$ 得：

$$0 = (k_2-k_1)x+(b_2 - b_1)$$ $$(b_1 - b_2) = (k_2-k_1)x$$ $$x=\dfrac{b_2-b_1}{k_1-k_2}$$

将 $x=\dfrac{b_2-b_1}{k_1-k_2}$ 代回原式：

$$y = k_1 \cdot \dfrac{b_2-b_1}{k_1-k_2} +b_1$$

证毕。

有这两个结论后，我们就可以思考一下方法了：

1. 直线去重。这是显然的，毕竟重复的会多算。
2. 枚举每一条线，计算其与之前线的交点。注意交点也要去重。注意：如果枚举到两条线斜率一致，就要过掉。因为它们没有交点。
3. 答案加上交点数加一，回到步骤二。

依照步骤实现即可。去重可以用 set。然后注意结果加一（平面初始就是一部分）。

代码

#include <iostream>
#include <map>
#include <set>
#define IL inline
using namespace std;
const int N = 1e5 + 10;

struct node
{
    long double k, b;
}a[N];

int main()
{
    int n;
    cin >> n;
    int m = 0;
    set<pair<long double, long double> > p;
    for(int i = 1;i <= n;i++)
    {
        long double x, y;
        cin >> x >> y; 
        p.insert({x, y});//set 去重。 
    }
    for(auto i = p.begin();i != p.end();i++) //遍历并存入结构体数组。 
    {
        a[++m] = {(*i).first, (*i).second};
    }
    int ans = 0;
	
    for(int i = 1;i <= m;i++)
    {
		set <pair<long double,long double> > o;
        for(int j = 1;j < i;j++)
        {
            long double k1 = a[i].k;
            long double k2 = a[j].k;
            long double b1 = a[i].b;
            long double b2 = a[j].b;
            if(k1 == k2) continue; //斜率一致，平行，过掉。 
            long double x1 = (b2 - b1)  / (k1 - k2);
            long double y1 = k1 * x1 + b1;
            //根据公式计算交点。
            o.insert({x1, y1});
            //加入 set 去重。
        }
        ans += (o.size() + 1);
    }
    cout << ans + 1 << endl; //初始有一部分，要加一。
    return 0;
}