自动搬运

查看原文

来自洛谷，原作者为

	Joton ILC

搬运于2025-08-24 22:41:18，当前版本为作者最后更新于2023-01-03 17:21:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这是本蒟蒻的第一篇题解，大佬轻点喷。

“约瑟夫环” （普及+/提高），这一看就不简单。

本题下标从 $0$ 开始编号

题目大意

有 $n$ 个人编号为 $1$，$2$，…… ，$n$，每当报道 $k$ 时的人退出游戏圈，不参与报数，下一个人从 $1$ 继续开始报数。

Algorithm 1 模拟 $O(nk)$

首先可以将人不断入队和出队，当有人报的数到达了 $k$ 时，就将其出队，而不继续入队，并且将报的数字归零。直到队列中只剩下了最后一个人为止。

下面是我的模拟代码，很显然时间复杂度太高了。

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int n,k;
    cin >> n >> k;
    queue<int> peo;
    for(int i = 1;i <= n;i++)
    {
    	peo.push(i);
    }
    int cnt = 0;
    while(peo.size() != 1)
    {
    	int name = peo.front();
    	cnt++;
    	if(cnt == k)
    	{
            peo.pop();
    		cnt = 0;
    		continue;
    	}
        peo.pop();
    	peo.push(name);
    }
    cout << peo.back();
    return 0;
}

Algorithm 2 使用约瑟夫环的递推公式 $O(n)$

设 $F(i)$ 为 $i$ 个人报数到 $k$ 就出局，最后剩下的人的编号。 初始状态 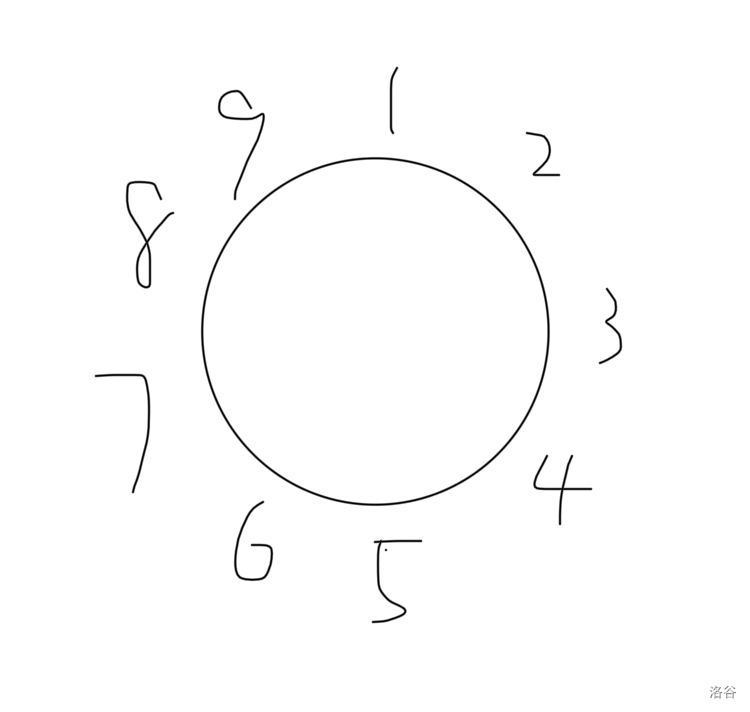第一次出队后 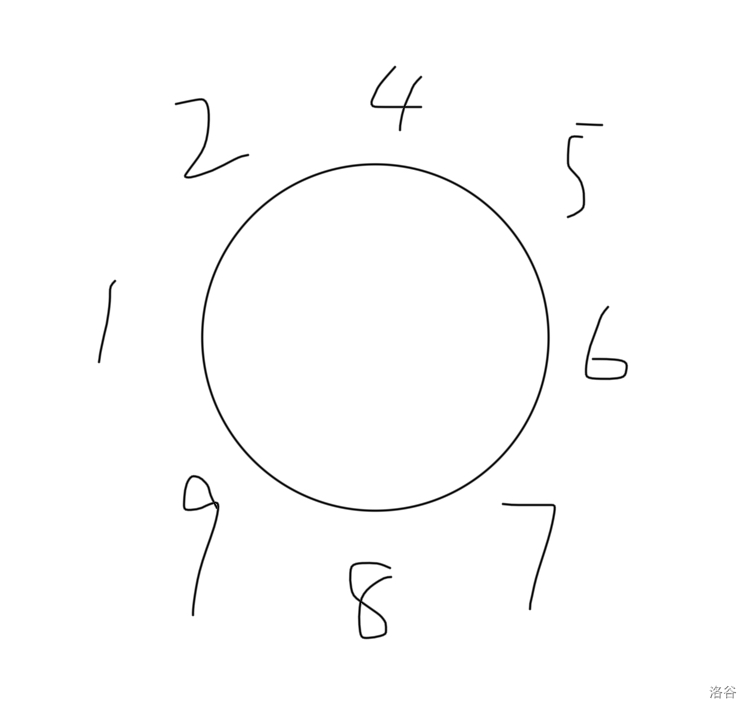第二次出队后 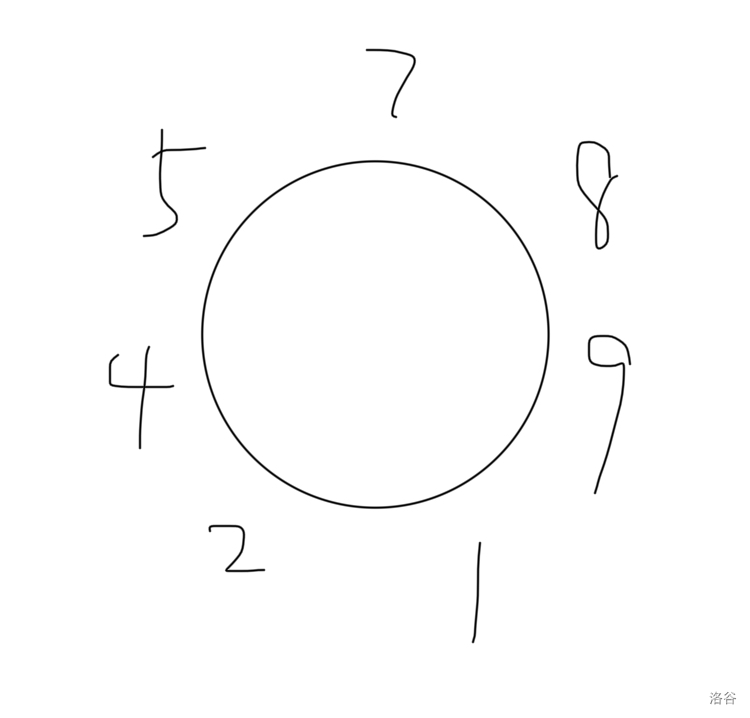每次出队一人，在约瑟夫环上的每个人都向前移动了 $k$ 位。 那么如果要反着来，就是每次加上一个人，在约瑟夫环上的每个人都向后移动了 $k$ 位。 易得剩下一个人的时候，最终答案对应的下标为 $F(1)=0$。 那么加上一个人，最终答案对应的下标就是 $F(2) = (F(1) + k) \bmod 2$。 再加上一个人，最终答案对应的下标就是 $F(3) = (F(2) + k) \bmod 3$。 以此类推， 那么可以得出递推公式：

• $F(1)=0$
• $F(n)=(F(n-1)+k)\bmod n$ 于是就可以求答案了。

#include <bits/stdc++.h>
 
using namespace std;

int main()
{
    int n,k,s = 0;
    cin >> n >> k;
    for(int i = 2;i <= n;i++)
    {
        s=(s+k)%i;
    }
    cout << s+1; //答案初始下标为1
    return 0;
}

题目传送门

鸣谢 @cqrcqr。