自动搬运

查看原文

来自洛谷，原作者为

	qhj0906 这个家伙不赖，但什么也没有留下

搬运于2025-08-24 22:40:58，当前版本为作者最后更新于2024-12-22 17:11:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先观察数据范围，发现 $n$ 的范围很小，可以直接压缩每一列的状态，就可以想到状压 dp，进一步的，可以想到轮廓线 dp。

在构建生成树的过程中,我们其实只关注每个点属于哪一个集合，更具体的，我们只关心每个点所在集合相互之间的关系，可以理解为联通块问题，直接用最小表示法维护轮廓线的状态。

具体如下图：

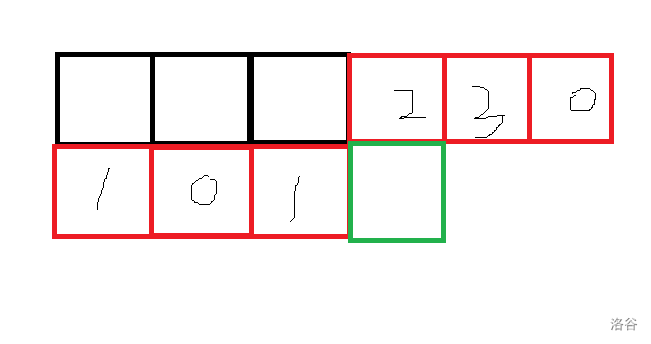
红色格子是维护的轮廓线， $0$ 表示无点，否则为点在目前轮廓线上所在的集合，相邻格子集合可以不同。

绿色是我们目前考虑到的格子。

为了方便，我们称绿点上面点的状态为 $S_u$，左面点状态为 $S_l$,绿点的状态为 $S_i$。

下面开始分类讨论

绿色无点

此时上点和左点都无法连边，也就是状态无法延伸。

关键点：注意到上点此时无法延伸，若此时上点在轮廓线上没有其他点和它处在同一集合,也就是 $S_u$ 唯一（如图），那么上点肯定无法和其他点保持联通，也就无法连成树了

所以要特判上点不联通的情况，否则将绿点置为 $0$。

绿色有点

有点就要考虑和上点和左点的连边。

连上连左

此时要特判 $S_u=S_l$ 的情况，此时会成环。

否则，暴力地修改轮廓线上和 $S_l$ 相等的点，改为 $S_u$。并将 $S_i$ 设为 $S_i$。

注意到状态更改时，可能就不符合最小表示法了，要暴力的推平重设状态。

上图状态就会变为

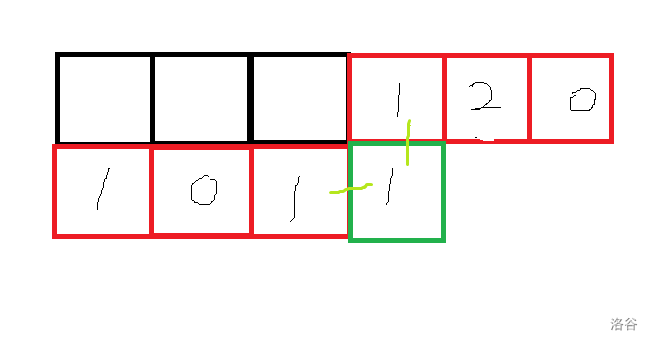
连上不连左

设 $S_i$ 为 $S_u$，其实轮廓线上状态没变。

连左不连上

设 $S_i$ 为 $S_l$，其实就是轮廓线上第 $i$ 位状态变为 $S_l$，注意判断上点是否联通和状态推平。

不连上也不连左

此时绿点一定在一个独立的集合，我们直接令 $S_i=7$ （轮廓线上肯定没有 $7$）

最后统计答案时只需要 dp 到最后一个点，保证最后轮廓线上要么 $1$ 要么 $0$。

状态保存可以 $8$ 进制压位。

推平重构就从前往后给没出现过的集合依次标号。

复杂度分析

可以爆搜得出 $n=6$ 是，合法状态有 $877$ 个，复杂度约为 $O(nmS)$ 跑不满但常数挺大，主要在推平重构，卡常可以开桶统计一下。

贴一下代码

#define N 1000010
#define max(x,y) (x>y?x:y)
#define sol(S,x) ((S>>(pre[x]))&7)
int ss[900],b;
int tot,id[N],vis[N];
int n,m,v[N][7],op,pre[7],st[2][900],top[2];
int dp[2][900];
void dfs(int x,int mx){
    if(x==n+1){
        ++tot;ss[tot]=b;id[b]=tot;
        vis[b]=b;
        return;
    }
    for(int i=0;i<=mx+1;++i){
        b|=(i<<pre[x]);dfs(x+1,max(mx,i));b^=(i<<pre[x]);
    }
    return;
}
void insert(int x,int y){
    if(!dp[op][x]){st[op][++top[op]]=x;}
    dp[op][x]=(dp[op][x]+y)%mod;
    return;
}
int vs[8],edx,edy,stx,sty;
int solve(int S){
    if(vis[S])return vis[S];
    memset(vs,0,sizeof(vs));
    int T=0,tot=0;
    for(int i=1;i<=n;++i){
        int y=sol(S,i);
        if(y&&!vs[y])vs[y]=++tot;
        T|=(vs[y]<<pre[i]);
    }
    vis[S]=T;
    return T;
}
int check(int S){
    for(int i(1);i<=n;++i)if(sol(S,i)>1)return 0;
    return 1;
}
signed main(){
    read(n),read(m);
    pre[0]=100;
    for(int i=1;i<=n;++i)pre[i]=(i-1)*3;
    dfs(1,0);
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            char c;cin>>c;
            if(c=='E')v[j][i]=1;
        }
    }
    for(int i(1);i<=m;++i){
        for(int j(1);j<=n;++j){
            if(v[i][j])edx=i,edy=j;
        }
    }
    insert(id[0],1);
    int ansl=0;
    for(int i=1;i<=m;++i){
        for(int j=1;j<=n;++j){
            op^=1;top[op]=0;
            int opp=op^1;
            for(int k=1;k<=top[opp];++k){
                int S=ss[st[opp][k]],z=dp[opp][st[opp][k]];dp[opp][st[opp][k]]=0;
                int y=sol(S,j),yy=sol(S,j-1),opl=0;
                if(!y)opl=1;
                else {
                    for(int k(1);k<=n;++k){
                        if(j!=k&&y==sol(S,k)){opl=1;break;}
                    }
                }
                if(!v[i][j]){if(opl)insert(id[solve(S^(y<<pre[j]))],z);}
                else{
                    if(y&&yy&&y!=yy){
                        int T=S;
                        for(int k=1;k<=n;++k){
                            if(yy==sol(S,k)){
                                T^=(yy<<pre[k]);
                                T|=(y<<pre[k]);
                            }
                        }
                        insert(id[solve(T)],z);
                    }
                    if(y)insert(id[S],z);
                    if(yy&&opl==1)insert(id[solve(((S^(y<<pre[j]))|(yy<<pre[j])))],z);
                    if(opl==1)insert(id[solve(((S^(y<<pre[j]))|(7<<pre[j])))],z);
                }
            }
            if(i==edx&&j==edy){ansl=1;break;}
        }
        if(ansl)break;
    }
    int ans=0;
    for(int i=1;i<=top[op];++i){
        if(check(ss[st[op][i]])){
            ans=(ans+dp[op][st[op][i]])%mod;
        }
    }
    writeln(ans);
    return 0;
}