自动搬运

查看原文

来自洛谷，原作者为

	chrispang 菜就是菜，怎么练都没用！|| 支持互关，规则见主页 || 禁止发接龙，发过来我会发回去 || 小号 1822435

搬运于2025-08-24 22:40:36，当前版本为作者最后更新于2025-08-11 21:07:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目大意

给出一棵树，设这棵树的直径长度为 $x$，则答案为：

树的结点数量不超过 $10^5$。

题目分析

我们可以考虑每一个节点 $x$，假设树中的直径经过 $x$ 且在 $x$ 子树中。那么树的直径长度应为：$x$ 子树中到达 $x$ 的最长路 $+$ $x$ 子树中到达 $x$ 的次长路。如图，粉色路径与橙色路径可以构成一条直径：

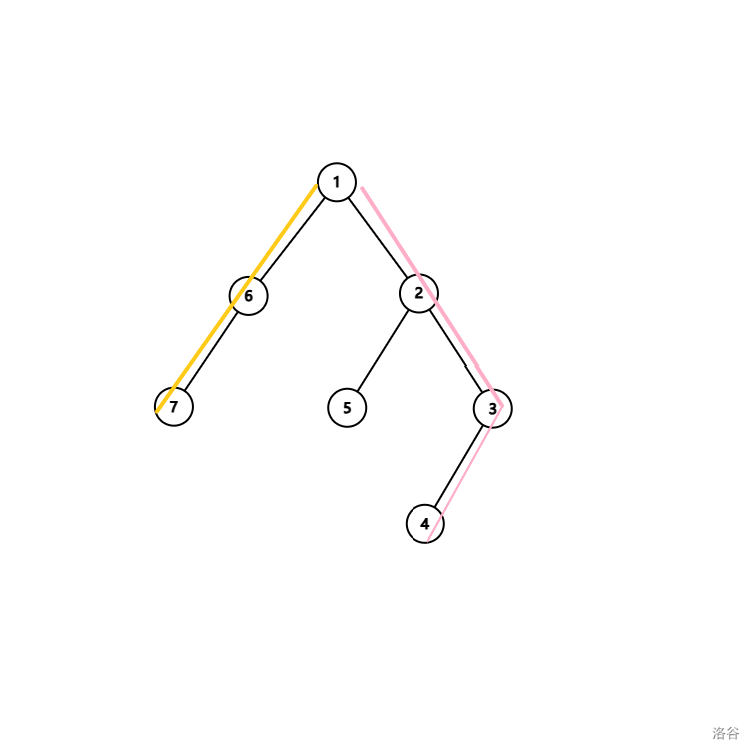
因此，我们可以考虑使用 DP 求出最长路与次长路：

• 状态：定义 $f_{i,0/1}$ 表示在 $i$ 的子树中，达到 $i$ 的最长路或次长路（$0$ 和 $1$ 分别表示最长路与次长路）

• 状态转移方程：

::::success[点我点我] 遍历 $i$ 的每个儿子，设 $i$ 到其儿子的距离为 $w$。分两种情况：

• 若 $f_{son,0}+w \ge f_{i,0}$，则 $f_{i,1}=f{i,0},f_{i,0}=f_{son,0}+w$。

• 若上述条件不满足，且 $f_{son,0}+w > f_{i,1}$，则 $f_{i,1}=f_{son,0}+w$。 ::::

• 初始化：每个叶子节点的 $f_{i,0/1}$ 设为 $0$。

• 答案：$\max_{i=1}^n\{f_{i,0}+f_{i,1}\}$。

代码实现

#include <bits/stdc++.h>
#define maxn 10010
using namespace std;

struct edge {
    int to, w;
};

int n, ans = -1e9, dis[maxn], f[maxn][2];
vector<edge> linker[maxn];
void add(int x, int y, int w) {
    linker[x].push_back({y, w});
}

void dfs(int x, int fa) {
    // 遍历每个儿子
    for (auto v : linker[x])
        if (v.to != fa) dfs(v.to, x);

    // 跑 DP，计算子树中的最长路和次长路
    for (auto v : linker[x]) {
        int son = v.to, w = v.w;
        if (son == fa) continue;
        if (f[son][0] + w >= f[x][0]) f[x][1] = f[x][0], f[x][0] = f[son][0] + w;
        else if (f[son][0] + w > f[x][1]) f[x][1] = f[son][0] + w;
    }
    ans = max(ans, f[x][0] + f[x][1]);
}

int main() {
    cin >> n;
    for (int i = 1; i < n; i++) {
        int x, y, w;
        cin >> x >> y >> w;
        add(x, y, w), add(y, x, w);
    }
    dfs(1, 0);
	cout << (ans * 10 + ans * (ans + 1) / 2) << endl;
	return 0;
}