自动搬运

查看原文

来自洛谷，原作者为

	NaCly_Fish 北海虽赊，扶摇可接。

搬运于2025-08-24 22:40:09，当前版本为作者最后更新于2022-10-06 08:12:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

以下复杂度分析中，均认为 $n,k,m$ 同阶。

题目中给出的「恰好 $m$ 个宝物」的条件有点难处理，先考虑一个简化的问题：求 $2\times n$ 的网格中放置 $k$ 个障碍物，使得最左侧和最右侧连通的方案数。

设 $a_{n,k}$ 为放置 $k$ 个障碍物，且最右侧两格不放障碍，使得最左侧和最右侧连通的方案数；类似地设 $b_{n,k}$，要求最右侧放一个障碍。

我们很快就能得到递推式（注意 $a_{0,0}=1$）：

$$a_{n,k}=a_{n-1,k}+b_{n-1,k}$$ $$b_{n,k}=2a_{n-1,k-1}+b_{n-1,k-1}$$

现在来考虑原问题，枚举和左边连通的块的最右端在哪，要注意的是和左边连通的块被截断时，会有三种情况：

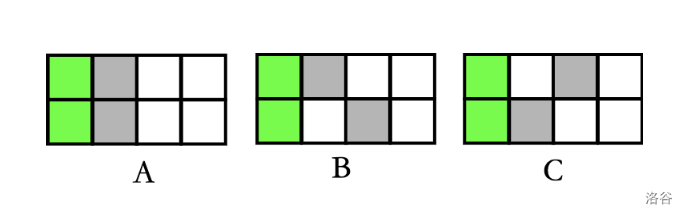
对于情况 A，截断连通块需要 $2$ 个障碍，右侧还有 $2\times(n-i-1)$ 个格子，可以随便放上 $k-(2i-m)-2$ 个障碍；而 B、C 两种情况是等价的，可以类比情况 A 来推出答案为：

$$[k=2n-m](a_{n,k}+b_{n,k})+\sum_{i=0}^{n-1}a_{i,2i-m}\binom{2(n-i-1)}{k-2i+m-2}+b_{i,2i-m}\binom{2(n-i)-1}{k-2i+m-1} $$

那个单独的项是因为地图的边界也是障碍，不需要放额外的障碍来截断。

当然我们不满足于 $\Theta(n^2)$ 递推计算 $a_{i,2i-m}$，注意到求和式中实际只用到了 $\Theta(m)$ 个 $a$ 的值，而且都是在一条斜线上的。为了找出可能的优化算法，我们尝试对 $m\geq 2$ 列出所有 $a_{i,2i-m}$ 非零项的值，再把每行翻转一下，得到了这样一个三角形：

1 
2
2 1
2 4
2 8 1
2 12 6
2 16 18 1
2 20 38 8
2 24 66 32 1

设其中第 $m$ 行（从 $0$ 开始计）的生成函数为 $F_m(x)$，将原始递推式化简为 $a_{n,k}=a_{n-2,k-1}+a_{n-1,k-1}+a_{n-1,k}$，映射到这个三角形上就是 $F_m(x)=F_{m-1}(x)+xF_{m-2}(x)+xF_{m-3}(x)$。

如果设其中第 $k$ 列（从 $1$ 开始计）的生成函数为 $C_k(x)$，就有：

$$C_k(x)=xC_k(x)+(x^2+x^3)C_{k-1}(x)=x^2\frac{1+x}{1-x}C_{k-1}(x) $$$$C_k(x) = x^{-2}\left( x^2\frac{1+x}{1-x}\right)^k$$

使用经典方法，设

$$g(x) = x \sqrt{\frac{1+x}{1-x}}$$

$h(x)=g^{\langle -1 \rangle}(x)$，则：

$$[x^m]\left( x^2 \frac{1+x}{1-x}\right)^k=[x^m]g(x)^{2k}=[x^{m-2k}]h'(x)\left( \frac{x}{h(x)}\right)^{m+1} $$

使用 FFT 就可以做到 $\Theta(n \log n)$，然而 $h(x)$ 是代数幂级数，这样一行的系数显然是微分有限的。使用 ODE 自动机，或直接算前几项后暴力高斯消元来得到整式递推式，都是可行的，时间复杂度 $\Theta(n)$。

细节巨大多，还是来贴一份 std，使用的是高斯消元法。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#define N 3000003
#define ll long long
#define reg register
#define p 998244353
using namespace std;

struct Z{
    int v;
    inline Z(const int _v=0):v(_v){}
};

inline Z operator + (const Z& lhs,const Z& rhs){ return lhs.v+rhs.v<p ? lhs.v+rhs.v : lhs.v+rhs.v-p; }
inline Z operator - (const Z& lhs,const Z& rhs){ return lhs.v<rhs.v ? lhs.v-rhs.v+p : lhs.v-rhs.v; }
inline Z operator - (const Z& x){ return x.v?p-x:0; }
inline Z operator * (const Z& lhs,const Z& rhs){ return (ll)lhs.v*rhs.v%p; }
inline Z& operator += (Z& lhs,const Z& rhs){ lhs.v = lhs.v+rhs.v<p ? lhs.v+rhs.v : lhs.v+rhs.v-p; return lhs; }
inline Z& operator -= (Z& lhs,const Z& rhs){ lhs.v = lhs.v<rhs.v ? lhs.v-rhs.v+p : lhs.v-rhs.v; return lhs; }
inline Z& operator *= (Z& lhs,const Z& rhs){ lhs.v = (ll)lhs.v*rhs.v%p; return lhs; }
inline bool operator ! (const Z& x){ return x.v==0; }

struct poly{
    Z a[8];
    int t;
    inline Z operator [] (const int& x) const{ return a[x]; }
    inline Z& operator [] (const int& x){ return a[x]; }

    inline Z eval(const int& x){
        Z res = a[t];
        for(reg int i=t-1;~i;--i) res = a[i]+res*x;
        return res;
    }
}P[8];

inline Z power(Z a,int t){
    Z res = 1;
    while(t){
        if(t&1) res *= a;
        a *= a;
        t >>= 1;
    }
    return res;
}


Z fac[N<<1],ifac[N<<1];

void init(int n){
    fac[0] = fac[1] = ifac[0] = ifac[1] = 1;
    for(reg int i=2;i<=n;++i) fac[i] = fac[i-1]*i;
    ifac[n] = power(fac[n],p-2);
    for(reg int i=n-1;i;--i) ifac[i] = ifac[i+1]*(i+1);
}

inline Z binom(int n,int m){
    if(n<m||m<0) return 0;
    return fac[n]*ifac[m]*ifac[n-m];
}

int ms,K;

void get_formula(Z *F,int n,int deg){
    ++n;
    int B = (n+2)/(deg+2),C = B*(deg+1),R = n-B+1,c = 0;
    Z mat[103][103],tmp[103];
    for(reg int i=0;i!=R;++i)
    for(reg int j=0;j!=B;++j){
        Z x = F[i+j];
        for(reg int k=0;k<=deg;++k){
            mat[i][j*(deg+1)+k] = x;
            x *= i+j;
        }
    }
    for(reg int i=0;i!=C;++i){
        int pt = -1;
        for(reg int j=c;j!=R;++j){
            if(!mat[j][i]) continue;
            pt = j;
            break;
        }
        if(pt==-1) break;
        for(reg int j=0;j!=C;++j) swap(mat[pt][j],mat[c][j]);
        Z w = power(mat[c][c],p-2);
        for(reg int j=i;j!=C;++j) mat[c][j] *= w;
        for(reg int j=c+1;j!=R;++j){
            if(!mat[j][i]) continue;
            Z t = mat[j][i];
            for(reg int k=i;k!=C;++k) mat[j][k] -= mat[i][k]*t;
        }
        ++c;
    }
    for(reg int i=c-1;~i;--i){
        if(!mat[i][c]) continue;
        for(reg int j=i-1;~j;--j) mat[j][c] -= mat[i][c]*mat[j][i];
    }
    int od = c/(deg+1);
    P[0][c%(deg+1)] = 1;
    for(reg int i=c-1;~i;--i) P[od-i/(deg+1)][i%(deg+1)] = -mat[i][c];
    for(reg int i=0;i<=od;++i){
        for(reg int j=0;j<=deg;++j) tmp[j] = 0;
        for(reg int k=0;k<=deg;++k){
            Z S = 1;
            for(reg int j=k;j<=deg;++j){
                tmp[k] += P[i][j]*S;
                S *= power(j+1-k,p-2)*(p-i)*(j+1);
            }
        }
        for(reg int j=0;j<=deg;++j) P[i][j] = tmp[j];
    }
    ms = od,K = deg;
}

inline Z query(int n,int k){ 
    Z res = 0;
    for(int i=0;i<=k;++i) res += binom(n,k-i)*binom(n+i-1,i);
    return res;
}

inline void get_row(int m,Z *r){
    static Z suf[N],ea[N];
    int len = m>>1;
    bool flag = len>19;
    for(int i=0;i<=min(len,19);++i) r[i] = query(len-i+1,m-2*(len-i));
    if(!flag) return;
    get_formula(r,19,5);
    suf[len] = Z(1);
    for(int i=len-1;i>=20;--i){
        ea[i] = P[0].eval(i);
        suf[i] = suf[i+1]*ea[i];
    }
    Z Inv = power(suf[20],p-2),pre = Z(1);
    for(int i=20;i<len;++i){
        Z tmp = -(P[1].eval(i)*r[i-1]+P[2].eval(i)*r[i-2]);
        r[i] = tmp*Inv*suf[i+1]*pre;
        pre *= ea[i];
    }
    r[len] = m==0?1:2;
}

int n,k,m,lf,lg;
Z f[N],g[N];
Z ans;

int main(){
    P[0].t = P[1].t = P[2].t = 5;
    scanf("%d%d%d",&n,&k,&m);
    init(n<<1);
    get_row(m-2,f),get_row(m-1,g);
    lf = m>>1,lg = m&1?(m>>1)+1:m>>1;
    for(int i=lg;i<m;++i) ans += f[i-lg]*binom((n-i-1)<<1,k-2*i+m-2);
    get_row(m-3,f);
    for(int i=0;i<lg;++i) g[i] += f[i];
    if(!(m&1)){
        ++lg;
        g[lg-1] = 2;
        for(int i=lg-2;i>0;--i) g[i] = g[i-1];
        g[0] = 0;
        for(int i=lg-1;i<=m;++i) ans += g[i-lg+1]*binom(2*(n-i)-1,k-2*i+m-1);
    }else
        for(int i=lg;i<=m;++i) ans += g[i-lg]*binom(2*(n-i)-1,k-2*i+m-1);
    if(k==(n<<1)-m) ans += query(n-k+1,k);
    printf("%d",ans.v);
    return 0; 
}