自动搬运

查看原文

来自洛谷，原作者为

	dottle Cy@?g|^a

搬运于2025-08-24 22:40:07，当前版本为作者最后更新于2022-09-05 18:17:58，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

⚠警告：题解非常摧毁本题的思考体验，作者强烈建议您先思考完题再来看题解

题目简述

对于一个排列，我们维护一个指针 $t$，初始为 $m$，每次从 $1\sim t$ 的元素中选一个没删过的删掉，若删掉的比上一个大且 $t<n$，则 $t$ 自增 $1$，否则结束此过程。你希望使得 $t=n$，且会使用最优的策略。

对于所有排列，求可以使得 $t=n$ 的概率，对 $998244353$ 取模。多次询问，每次给出一个 $m$。

构建映射

首先，明确一点。我们总是会标记比上一次标记的大的最小的那个数，如果没有比就寄了。

为了方便直观理解，我们把 $i$ 当作大小为 $i$ 的积木，删掉一个数就把他搭在地上，当我们寄掉的时候，将那些 $1\sim t$ 的还没标记的数按照原排列中的顺序搭起来。最后我们会搭出一个积木塔。

我们考虑 $\bm{t\ne n}$ 的概率，这一点非常重要。如果你认为后文的积木塔还可能有其他的形态，请再思考一下这句话。后文 $(\star)$ 性质用到了这一性质。

先来考虑 $m=1$ 时我们搭出来的积木塔长啥样：不断增大，在最后一个位置减小 $(\star)$。我们称这个形态为“基本积木塔”。这里如果不保证没取完的话，有可能整个数列都是递增的，就不好办了。

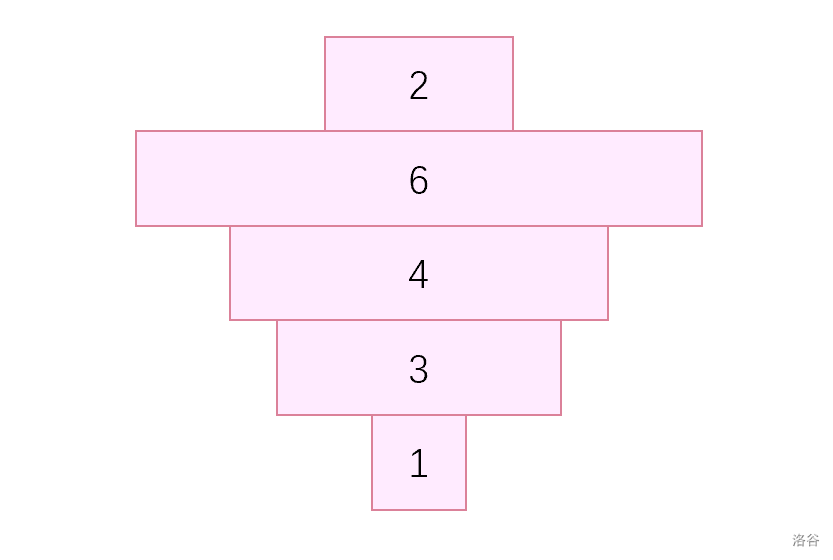
再来考虑 $a_i=2$ 时候长什么样子。我们对于一个例子来分析：对于 $\{1,4,2,8,5,7,3,6,9,10\}$，我们搭出来应该是 $\{1,2,4,5,7,8,3,6\}$。我们还是把塔画出来，然后给塔染色：

1. 对于原序列的前 $m$ 个积木，染上不同的颜色。
2. 若我们搭了一个颜色的积木 $c$ 后，指针新移动到的位置对应的积木也染成 $c$。
3. 为每个颜色确定标号，倒数第 $m$ 个积木的颜色编号为 $1$，倒数第 $m-1$ 个染成 $2$，以此类推，最后一个积木染色成 $m$。

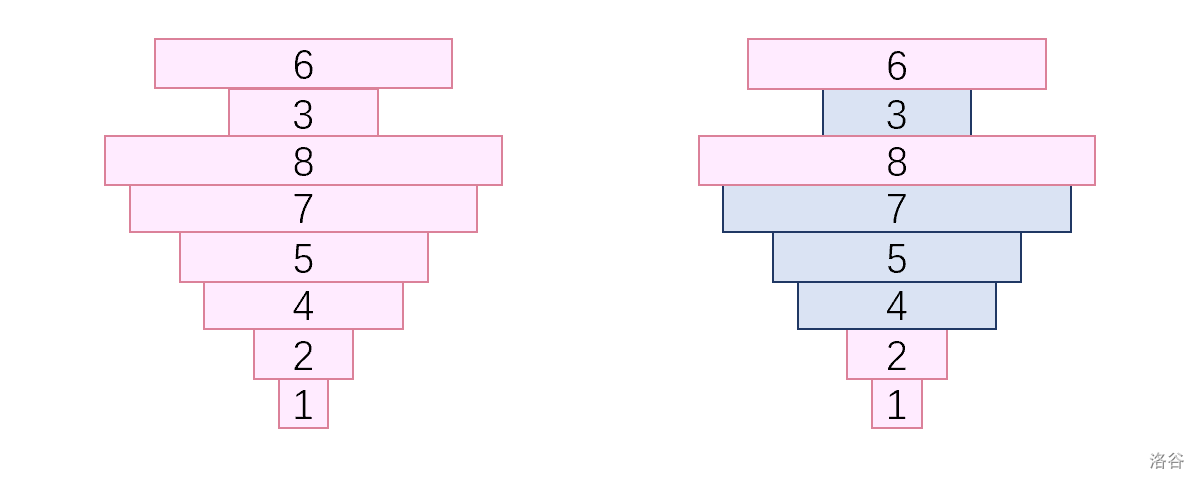
右边是染色后的结果。蓝色为 $1$，粉色为 $2$。值得注意的是，因为我们新移动到的数的颜色与我们标记的颜色相同，因此在每个时刻，我们手上每个颜色的数都有恰好一个。

我们染色的目的是展示这样一个事实：

• 一个数列对应的 $m=2$ 的塔可以唯一划分为两个 $m=1$ 的塔，并为他们确定标号。
• 两个确定好标号的 $m=1$ 的塔也能唯一归并出一个已染色的 $m=2$ 的塔。归并的方式是，每个塔除去最后一块的部分，按照大小排序；每个塔的最后一块，按照标号排序。

然后，我们再来讨论原数列与已染色的 $m=2$ 的塔的对应关系，我们已经介绍了通过数列唯一构造已染色的塔的方法了，我们再来考虑用塔构造数列前 $l$ 项的方法（$l$ 是塔的高度）。

1. 根据各个颜色第一个的数，可以求出数列的前 $m$ 项的集合，对应了 $m!$ 种排列。这个 $m!$ 的系数我们不急着考虑，最后再来乘。
2. 取出比上一个放的积木更大的积木中最小的那个，把下一个此颜色的积木放在序列尾，然后更新你手上积木的集合。

其他 $n-t$ 个数可以任意排，所以已染色的塔可以对应 $(n-t)!$ 个数列。

我们发现这些步骤对于 $m>2$ 也成立，那么就很好了。在此，我们再来检视一下我们构建的映射：$m$ 个基本积木塔的任何归并都对应一个已染色的积木塔，从而对应 $(n-t)!$ 个数列。

开始计数

考虑 $i$ 个数，将他们搭成基本积木塔的方案数为 $i-1$，即选择一个放到最后面。因此基本积木塔的 EGF 为：

$$f(x)=\sum_{i\ge1}\frac {(i-1)x^i}{i!}$$

则固定 $m$，积木塔的 EGF 为 $f^m$。那么我们要求的变为：

$$\sum_{i=m}^{n-1}i![x^i]f^m(x)(n-i)!\binom ni =n!\sum_{i=m}^{n-1}[x^i]f^m(x)=n![x^{n-1}]\frac {f^m(x)}{1-x} $$

乘 $i!$ 是因为 EGF，乘 $(n-i)!$ 是因为高为 $i$ 的积木塔对应了 $(n-i)!$ 个数列，称组合数是因为我们要从 $n$ 个数里面选出 $i$ 个搭塔。

至此，可以一次多项式 exp 解决 $q=1$ 的部分分。

上面是搭不成功的概率，那么成功的概率就是：

$$\begin{aligned} &\phantom{={}}1-[x^{n-1}]\frac{f^m}{1-x}\\ &=1-[x^{n-1}]\frac{(e^xx-e^x+1)^m}{1-x}\\ &=1-[x^{n-1}]\sum_i{m\choose i}\frac{(e^x(x-1))^i}{1-x}\\ &=[x^{n-1}]\sum_{i\geq 1}{m\choose i}e^{ix}(x-1)^{i-1}\\ &=[x^{n-1}]\sum_{i\geq 1}{m\choose i}e^{ix}\sum_j{i-1\choose j}x^j(-1)^{i-1-j}\\ &=\sum_{i\geq 1}{m\choose i}\sum_j{i-1\choose j}[x^{n-1-j}]e^{ix}(-1)^{i-1-j}\\ &=\sum_{i\geq 1}{m\choose i}\sum_j{i-1\choose j}\frac{i^{n-1-j}}{(n-1-j)!}(-1)^{i-1-j}\\ \end{aligned} $$

至此，可以 $O(n^2)$ 预处理后面半截，单次 $O(n)$ 的询问。结合上文 $q=1$ 的部分分可以获得 $90$ 的高分。

#include<bits/stdc++.h>
#define ll long long
const int N=20005,mod=998244353;
using namespace std;

ll gsc(ll x,ll y){
    ll ans=1;
    for(int i=1;i<=y;i<<=1,x=x*x%mod)
        if(y&i)
            ans=ans*x%mod;
    return ans;
}int inv(int k){return gsc(k,mod-2);}
ll jc[N],ij[N],iv[N]; 
void init(){
    iv[0]=jc[0]=ij[0]=iv[1]=1;
    for(int i=2;i<N;i++)
        iv[i]=mod-(mod/i)*iv[mod%i]%mod;
    for(int i=1;i<N;i++)
        jc[i]=jc[i-1]*i%mod,ij[i]=ij[i-1]*iv[i]%mod;
}

int n,q,vis[N],m;
ll f[N];int C[N];

int chk(int k){
	return k>=mod?k-mod:k;
}

void solve(){
	cin>>n>>q,m=n/2;
	while(q--){
		int x;cin>>x;
		vis[x]=1;
	}
	init(); 
	C[0]=1;
	for(int i=1;i<=m;i++){
		ll pwi=gsc(i,n-1),p=iv[i];
		for(int j=0;j<i;j++){
			f[i]+=((i+j+1)&1?-1:1)*pwi*C[j]%mod*ij[n-1-j];
			f[i]%=mod;
			pwi=pwi*p%mod;
		}
		f[i]=(f[i]%mod+mod)%mod;
		for(int j=i;j;j--)
			C[j]=chk(C[j]+C[j-1]);
	}
	memset(C,0,sizeof(C));
	C[0]=1;
	for(int i=1;i<=m;i++){
		unsigned ll res=0;
		for(int j=i;j;j--){
			C[j]=chk(C[j]+C[j-1]);
			res+=C[j]*f[j];
			res%=mod;
		}
		res=res%mod+mod;
		if(vis[i])cout<<res%mod<<'\n';
	}
	for(int i=m+1;i<=n;i++)
		if(vis[i])cout<<1<<'\n';
}
main(){solve();}

设 $g_i=\sum_j{i-1\choose j}\frac{i^{n-1-j}}{(n-1-j)!}(-1)^{i-1-j}$，那么上式便是关于 $m$ 的卷积。

设 $a_i=\frac{(-1)^{i+1}}{(i-1)!(n-i)!}$ ，则 $g_i=(-1)^{i-1}\sum_j a_{j+1}(i-1)^{\underline j}i^{n-1-j}=\frac{(-1)^{i-1}}{i}\sum_j a_{j}i^{\underline {j}}i^{n-j}$

设 $f(x)=\sum_j a_{j}x^{\underline {j}}x^{n-j}$ ，则 $g_i=\frac{(-1)^{i-1}}{i}f(i)$

那么如果我们求出了 $f$ ，只需要一个 多 点 求 值 就可以得到 $g$ 。

考虑分治，设 $A_{l,r}=\prod_{l\leq i<r} (x-i)$ ，$B_{l,r}=\sum_{l\leq i<r} a_iA_{l,i}x^{r-1-i}$ 那么答案就为 $B_{0,n+1}$

考虑合并，有 $A_{l,r}=A_{l,mid}*A_{mid,r}$ ，$B_{l,r}=x^{r-mid}B_{l,mid}+A_{l,mid}*B_{mid,r}$

边界为 $A_{i,i+1}=x-i$ ，$B_{i,i+1}=a_i$

最后用一次卷积得到每一个 $m$ 的答案，总时间复杂度 $O(n\log^2 n)$。