自动搬运

查看原文

来自洛谷，原作者为

	EnofTaiPeople MGXS

搬运于2025-08-24 22:39:54，当前版本为作者最后更新于2022-11-13 13:58:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Part1 前言

题意需要我们维护一棵静态树，$\text{rake}$ 和 $\text{compress}$ 都需要通过调用函数实现，查询到节点 $x$ 距离不超过 $d$ 的边集信息，且每次查询只能进行一次信息合并，$n\le2\times10^5,q\le10^6$。

这道题太神了，以致于在 NOI2022 出现后被加入 Ynoi2003，这里感谢 zx2003，让我发现之前学的点权和 $\text{Top Tree}$ 真的只是简单应用。

Part2 $\text{Top Tree}$ 维护边集的静态构建

这道题的本质是 $\text{Top Tree}$ 上换根 dp，为了方便转移和查询，我们需要将 $\text{Top Tree}$ $\text{leafy}$ 化，使得每一条边所对应节点都是叶子，然后参照全局平衡二叉树的建立方式，注意节点 $1$ 没有父边，所以要忽略掉。

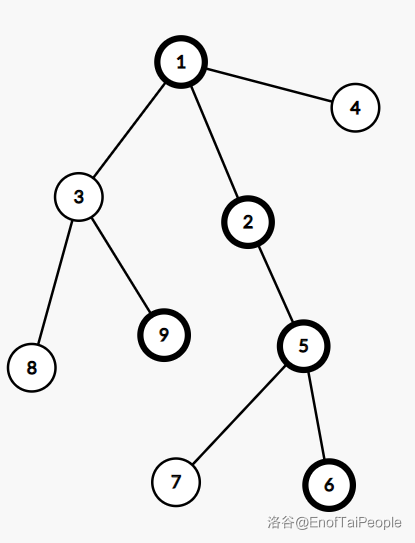
上图是一棵树，加粗的点表示重儿子，它所对应的 $\text{leafy-top-tree}$ 如下图：

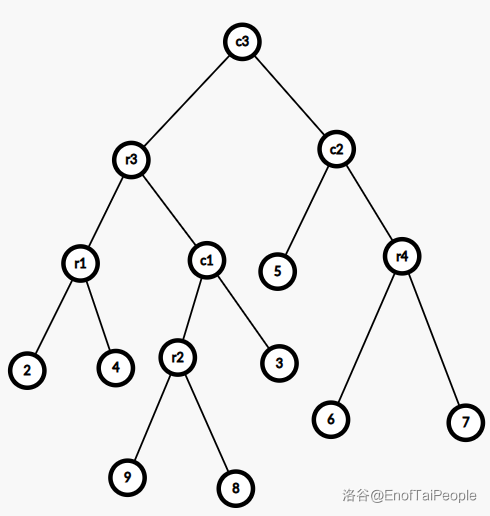
其中 $r1\sim r4$ 表示 $\text{rake-node}$，$c1\sim c3$ 表示 $\text{compress-node}$，容易发现，它是一棵二叉树，有 $2n-3$ 个节点。

Part3 对簇内信息的记录

簇其实就是连通的边集，并且有两个端点，上图的 $\text{Top Tree}$ 中，每一个节点都表示了一个簇。

如何维护簇内信息？

记 $g(x,0/1,k)$ 表示到左右端点距离为 $k$ 以内的边集信息。

对于一个 $\text{rake-node}$，左端点的信息就是两颗子树对应距离 $\text{rake}$ 得到的结果，由于建树时默认重儿子在左子树，所以右端点会继承左子树的右端点，自然也会继承左子树的右端点邻域信息。

对于每一个节点，维护一个 $len$，表示簇的左右端点距离，这样继承之后会将右儿子的 $k-len$ 邻域信息并进来：

ln[x]=ln[ls],U[x]=U[ls],V[x]=V[ls];
for(i=0;i<=rz[x];++i){
	g[x][0][i]=R(G(ls,0,i),G(rs,0,i));
	g[x][1][i]=R(G(ls,1,i),G(rs,0,i-ln[x]));
}

对于一个 $\text{compress-node}$，左端点是左儿子的左端点，右端点是右儿子的右端点，合并时 $len$ 会相加，同样在处理左/右端点信息时取的是右/左儿子的 $k-len$ 邻域信息：

ln[x]=ln[ls]+ln[rs],U[x]=U[ls],V[x]=V[rs];
for(i=0;i<=rz[x];++i){
	g[x][0][i]=C(G(ls,0,i),G(rs,0,i-ln[ls]));
	g[x][1][i]=C(G(ls,1,i-ln[rs]),G(rs,1,i));
}

由于每一个节点只会保留边数的信息，而此树具有全局平衡的性质，所以时空复杂度 $O(n\log_2n)$，这样就可以通过 $u=1$ 和 $n\le2000$ 的测试点了，具体地，可以对于每一个需要的根节点建一棵树，由于根节点必定是根簇的左端点，所以可以直接查询簇内信息，可以得到 $30pts$，时空复杂度 $O(rn\log_2n)$，$r$ 表示查询的不同节点个数。

Part4 对簇外信息的记录

发现对于一个节点，如果不是根簇端点，可能会很尴尬：从叶子往上跳，跳多了得到的信息就超了，跳少了信息又不完全，我们无法做到让查询的信息总在一个簇内与簇的某一端点完全相邻，于是需要记录簇外的信息。

记 $h(x,0/1,k)$ 表示 $x$ 的簇外到左/右节点距离为 $k$ 以内的邻域信息。

无论是哪一个节点，它的簇外信息都有两部分组成：父亲的簇外信息和兄弟的簇内信息，这方面不难推导，依旧只需要对于两种类型的节点分类讨论就可以了：

if(tp[x]){
	h[ls][0].resize(rz[x]+1);
	h[ls][1]=h[rs][0]=h[ls][0];
	h[rs][1]={emptyinfo};
	for(i=0;i<=rz[x];++i)
		h[ls][1][i]=H(x,1,i);
	for(i=0;i<=rz[x];++i){
		h[ls][0][i]=R(G(rs,0,i),H(x,0,i));
		h[rs][0][i]=R(C(G(ls,0,i),H(ls,1,i-ln[ls])),H(x,0,i));
	}
}else{
	h[ls][0].resize(rz[x]+1);
	h[rs][0]=h[ls][1]=h[rs][1]=h[ls][0];
	for(i=0;i<=rz[x];++i){
		h[ls][0][i]=H(x,0,i);
		h[rs][1][i]=H(x,1,i);
		h[ls][1][i]=C(H(x,1,i-ln[rs]),G(rs,0,i));
		h[rs][0][i]=C(H(x,0,i-ln[ls]),G(ls,1,i));
	}
}

大家可能发现了，对于每一个节点的簇外信息，我们都将其保留到了父亲的大小，这样可以方便查询。

具体地，从查询节点开始跳，直到父亲的簇大小超过 $d$ 为止，这样当前的簇内信息必定被完全包含，簇外信息也必定经过了预处理，可以通过两次 $\text{compress}$ 得到答案。

容易发现，这一部分必定会完全包含簇内信息，所以在预处理时将 $h(x,0,k)$ 与 $g(x,0,sz_x)$ 合并，就能保证查询时只需要一次 $\text{compress}$ 了，符合题意要求，时空复杂度 $O(n\log_2n)$。

Part5 代码效率说明

首先，这是我的第一次提交记录，也推荐大家参考，因为没有删注释，但是只有 $97$ 分，因为交完之后，我发现在本地纯随机造树就卡成了 too many MR,MC operations in init()，然后就莫名其妙地 Hack 成功了，后来发现这是被卡常了，微调了一下建树过程，就通过了，或许是出题人并不想卡人？反正目前是最优最短解，指不定哪一天就被人挤下去了。

然而，这样的做法又被我自己 Hack 掉了，原因是，当数据为一棵完全二叉树时，高度会达到 $60$，或许在时间上没有问题，但函数调用次数会大大增加，超过了 $3\times10^7$，所以需要进一步卡常，具体地，在 dp 时不需要处理到边集大小，只需要处理到直径就可以了。

Part6 后记

不知道自己想干什么，学一道题目花了一个星期，或许这是我联赛之前的最后一次任性吧。但这道题真的十分有教育意义，将树上问题在链和子树的基础上，又向全新的“邻域”问题发展，也让我了解到了 $\text{Top Tree}$ 的更多功能。