自动搬运

查看原文

来自洛谷，原作者为

	Undead2008 。

搬运于2025-08-24 22:39:46，当前版本为作者最后更新于2023-10-09 20:27:16，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目

题目描述

Khong 阿姨花了 $q$ 天时间准备糖果盒。在第 $j$ 天，对于每个编号满⾜ $l[j] \leq k \leq r[j]$ 的盒⼦ $k$：

• 如果 $v[j] > 0$，如果该盒⼦ $k$ 之前已有 $p$ 块糖果，那么在这次操作之后盒⼦将有 $\min(c[k], p + v[j])$ 块糖果。

• 如果 $v[j] < 0$，如果该盒⼦之前已有 $p$ 块糖果，那么在这次操作之后盒⼦将有 $\max(0, p + v[j])$ 块糖果。

你的任务是求出 $q$ 天之后每个盒⼦中糖果的数量。

$1\le n,q\le 2\times 10^5$

题目分析

以下均用 $a$ 代指原序列。

如果不考虑上下界的话，就是一个朴素的线段树问题。

棘手的是每一个位置都有独特的上界，没办法直接维护。

如果位置 $j$ 在某一时刻的值 $a_j=0$，就说它碰了下壁；如果位置 $j$ 在某一时刻的值 $a_j=c_j$，就说它碰了上壁。在最后一次碰壁后，上下界就没有作用了。因此，我们只需要知道最后一次碰壁的时间，就可以很方便地维护答案。

维护“时间”可以离线询问，将每一个操作的贡献打到时间轴上。将不考虑上下界后得到的时间轴记作 $b$。对于每一个位置 $j$，如果第 $i$ 个操作将 $b_j$ 加上了 $\Delta$，就相当于将 $b_j$ 在时刻 $i$ 到时刻 $q$ 内的每一个时刻的值都加上了 $\Delta$。

建立 $n$ 棵线段树维护每一个位置的时间轴 $b$ 是不现实的。可以使用类似差分的做法，将一个区间操作拆成两个对后缀的操作，即将 $(l,r,\Delta)$ 拆成 $(l,n,\Delta)$ 和 $(r+1,n,-\Delta)$，考虑扫描线思想，用一棵维护时间轴的线段树从左到右扫，到每个位置时都进行该位置上的操作（即到 $j$ 时进行所有 $(j,n,\Delta)$ 操作），这样执行完位置 $j$ 的所有操作后，线段树维护的就是位置 $j$ 的时间轴 $b_j$。

注意到如果一段时间内 $b_j$ 的极差（最大值减去最小值）大于等于 $c_j$，则 $j$ 至少碰壁一次。如果在这段时间内的时刻 $u$ 时 $b_j$ 取最大值，时刻 $v$ 时 $b_j$ 取最小值，则在时刻 $\max(u,v)$ 时 $j$ 一定碰壁 $^\dag$。不管 $\min(u,v)$ 是否碰壁，$\max(u,v)$ 往上走和往下走都会碰壁。

$^\dag$：这和大多数题解“时刻 $u$ 和时刻 $v$ 都会碰壁”的结论不同。后者在下图图 $4$ 中的两种情况中是明显错误的。

（蓝线代表考虑上下界后 $b_j$ 的值，红线代表不考虑上下界时 $b_j$ 的值）

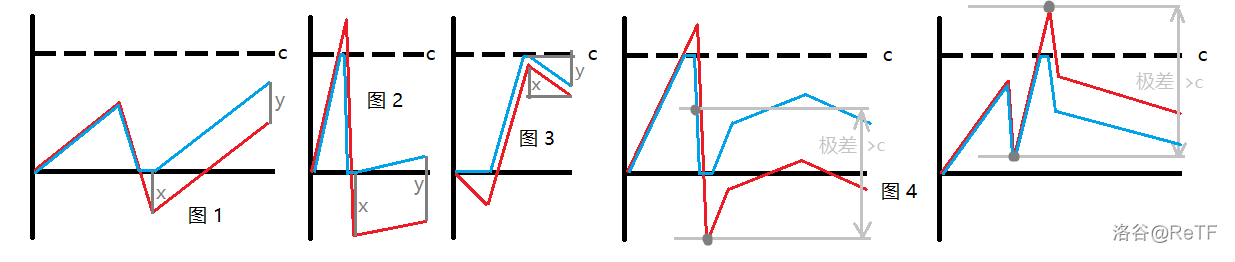
我们要找 $j$ 的最后一次碰壁，也就是要找时间轴上极差 $\ge c_j$ 的最短后缀。线段树的每个节点维护区间最大值，最小值时，这可以在线段树上二分实现。

记时刻 $q$ 时 $b_j$ 的值为 $f$，有三种情况：

• 找不到满足要求的后缀（对应上图 $1$），则答案等于 $f$ 减去整个时间轴每个时刻中 $b_j$ 的最小值。

否则，记 $U$ 和 $V$ 为满足要求的后缀中的最大值和最小值。

• $U$ 比 $V$ 先出现（对应上图 $2$）则答案等于 $f-V$；
• $V$ 比 $U$ 先出现（对应上图 $3$）则答案等于 $c_j-(U-f)$。

注意到前 $3$ 张图上的 $x$ 总等于 $y$，可以根据这个性质推出答案。

这道题就做完了。

代码实现

我写了一个带区间操作的线段树，代码或许会长出去好多。

线段树的每个节点维护区间最大值、最小值、懒标记和（叶子结点的）值即可。

代码