自动搬运

查看原文

来自洛谷，原作者为

	Elegia irony

搬运于2025-08-24 22:39:36，当前版本为作者最后更新于2022-09-05 10:37:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

好像有人想要一份更详细一点的题解, 我这里帮出题 青蛙 人写一下吧. 主要叙述通向正解的一些关键点, 所以内容会比本来讲题的课件里少一点.

理解题目

首先要说明的是注意到题意中两个操作的自然性, 所谓的 R 和 C 实际上就是 rake 和 compress 的缩写. 为什么说这两个操作是自然的呢? 因为它几乎就是所谓的 "动态 DP" 支持维护的信息合并的最一般形式了. 按照比较广为人知的方式解释就是, compress 无非是维护链上信息的合并, rake 是将子树信息附着在父亲链上. 此外值得一提的是, 再加上 "twist" 操作则是我们在广义串并联图上能实现的 DP 的信息合并. 在这里附上一张陈年老图:

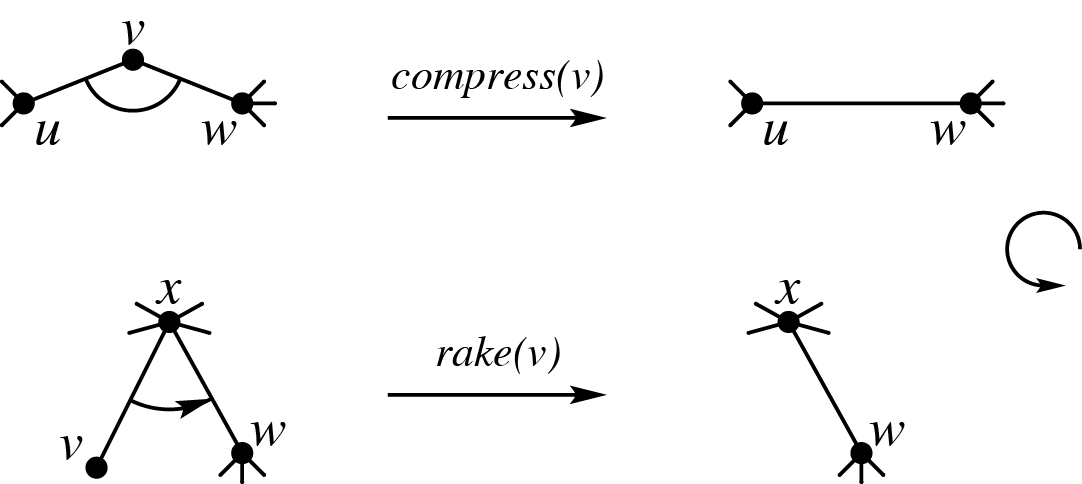
但也要注意到为了让题目的定义不变得长, 实际上对于信息合并的细节稍微牺牲了一点直观, 也就是一般来说应该是要允许只有一个端点的信息的. 在我们 rake 一个 $\epsilon$ 和一个信息的时候, 按照我们常见的理解应该是返回一个端点的信息, 但在这里不是. 对此可能某些实现时候在这里需要更加精细地处理, 比如用一个结构体把题目给的信息套起来.

树上 DP

我们需要支持有一些序列 $a$, 支持:

• 给出一个信息 $x$, 将所有信息 $a_i$ 变成 $C(x, a_i)$, 然后把 $x$ 放在序列的开头.

• 将两个序列 $a, b$ 合并, 其中先把较短的那个序列用它的最后一个元素补齐, 然后合并成 $R(a_i, b_i)$.

我们直接按照定义对上面的东西暴力 $O(n)$ 做, 就可以求出 $u=1$ 的答案.

自顶向下的时候处理一下前缀和后缀, 就可以 $C_1=O(n^2)$, $C_3=0$ 的情况下求出所有答案了. 此外少加修改, 我们如果只将序列长度保留到 $d$, 就可以完成子任务 C, 因为此时有 $C_1 = O(nd)$.

长链剖分

特殊性质 B 的解法和正解之一有较大的关系. 其实这部分实际上也比较熟知了, 这里仅复述大致思路.

简单来说, 对于前面的树形 DP 问题, 注意到只在所有操作的最后询问. 如果我们总是能 $O(1)$ 支持第一个操作, 并 $O(\min(|a|, |b|))$ 完成第二个操作, 根据简单的贡献分析, 总共的复杂度就是 $O(n)$ 的.

具体的实现是将一个序列实际开成两个数组 $p, q$, 其中一个可以看做某种惰性标记, 实际的 $a_i = q_1 C q_2 C \cdots C q_i C p_i$. 经过较为精细的实现, 就可以完成满足上述复杂度的维护了.

这样我们可以在 $C_1 = O(n), C_3 = 0$ 的情况下通过子任务 B 了.

树的簇 (cluster) 分解

或者说是最为标准的树分块方法. 我们实际上划分的不是树的点集而是边集. 我们称一个连通边集且仅有不超过 $2$ 个界点时是簇 (cluster). 这里界点就是和其他边有交的点. 把边集划分成若干个不交簇的并称为簇分解.

$2$ 个界点的限制, 实际上就是为了让簇分解看成是将树 "收缩" 成了一颗更小的树. 我们总可以将 $1$ 个界点的簇随便补一个界点, 然后将每个簇看做是两个界点间的一条"边".

我们这里还要用到簇的一个性质, 就是可以我们总可以将一颗树划分成 $O(n/d)$ 个大小不超过 $d$ 的簇. 对于这道题来说可能更弱一些, 我们只需要将树划分成 $O(n/d)$ 个直径不超过 $d$ 的簇. 对着这个事实来编一个构造划分的算法其实并不难, 基本上就是一个贪心, 细节在这里略去.

我们考虑固定 $d$ 的时候如何处理所有 $u$ 的询问. 首先将树划分成 $O(n/d)$ 个直径不超过 $d$ 的簇, 当我们询问一个点 $u$ 的时候, $u$ 必然在某个簇的点集内, 由于这个簇的直径不超过 $d$, 所以 $d$-邻域必然完全覆盖这个簇里的所有边! 如果我们已经处理了簇的信息为 $x$, 我们还对于每个簇的界点, 预处理出了两个界点外部子树的信息 $p, q$, 就可以通过计算出 $u$ 到两个界点的距离, 然后将询问的答案表为一个 $p_i C x C q_j$ 了!

我们可以先将每个簇处理出和深度有关的 "大信息", 这是可以通过前述的长链剖分做到 $O(d)$ 的. 然后, 界点外部的信息就可以通过在外面对 "大信息" 做 $O(n/d)$ 个界点构成的边上的树形 DP 来进行维护了. 这样的总复杂度是 $O(n/d)\cdot O(d) = O(n)$.

正解 1 -- 簇内与簇间 DP

我们发现, 前面的处理方法实际上略加修改就可以回答不止一个 $d$. 对于所有 $d\in [L, R]$ 的询问, 我们可以将树分成 $O(n/L)$ 个簇, 然后树形 DP 时候的信息量保留到 $O(R)$, 就是 $O(nR/L)$ 的复杂度进行预处理.

也就是说对每个 $k$, 我们可以 $O(n)$ 预处理 $d\in [2^k, 2^{k+1})$ 的询问. 那么我们就有 $C_1 = O(n\log n), C_3 \leq 1$ 了.

本人实现的就是这种做法, 不过似乎由于某些常数原因, 我需要开成 $4$ 为底数才能获得 $100$ 分.

正解 2 -- top cluster 分解

我们考虑将一颗树每次将两条边进行 rake/compress 让树越来越小的过程, 这个过程整个可以表示成一颗树的结构, 以及所谓的 "top tree". 对于 top tree, 我们可以通过很自然的方式截取出一个簇分解: 拿出 top tree 中大小不超过 $d$ 的所有极大子树.

但是这样的簇的数量能有保证吗? 显然对于随便建的 top tree 是没有的, 但可以证明, 按照全局平衡二叉树的方式构建的 top tree, 能够保证它给出的大小不超过 $d$ 的簇分解有 $O(n/d)$ 个簇.

这样一来, 我们可以直接在这个 top tree 上先自底向上维护出每个簇的簇内信息, 再自顶向下对每个 $d=2^k$ 维护出簇外信息.

这样也足够通过本题, 并且避免了长链剖分的细致讨论.

正解 3 -- 一个更精简的做法

我们忘掉 $[2^k, 2^{k+1})$ 的划分方式, 转而考虑一颗 top tree 本身天然给出的划分.

处理一个询问 $(u, d)$ 的时候, 我们可以先定位到这个点所在的大小不超过 $d$ 的最大子树, 此时 $(u,d)$ 邻域必然是覆盖住这个整个子树所代表的簇的, 而且此时 $d$ 一定小于这个子树的父亲子树的簇的大小.

我们将上一个解法中的自顶向下部分改成: 每个子树维护的簇外信息截取到其父亲的大小, 这样一来, 预处理的信息量实际上就是 $O\left(\sum_{u \in \mathrm{Toptree}} \mathrm{Sub}(u)\right)$, 换句话说, 就是这棵树的 "分治复杂度".

至此我们又丢掉了一个需要的性质, 现在的结论就是: 只要有一个分治复杂度为 $O(n\log n)$ 的, 且分治时只有 $\leq 2$ 个界点的结构, 就给出一个 $C_1 = O(n\log n)$, $C_3\leq 1$ 的处理方法.

当然全局平衡二叉树依然是满足这个条件的, 遗憾的是普及度最高的点分治并不适合处理这个问题, 因为它的分治过程有 $O(\log n)$ 个界点, 这是不构成 top tree 的结构的.

复杂度的最优性

我们最后证明一下在询问只允许 $1$ 次信息合并的时候, 预处理必须有 $\Omega(n\log n)$ 的合并次数, 事实上我们可以证明一条链的情况就已经有此下界.

为了叙述方便, 我们在链上直接说查询 $[l, r]$, 显然这和原问题是相差常数倍等价的. 我们记 $S_{[d/2, d]}$ 为所有点 $x$ 满足预处理的时候得到过一个以 $x$ 为一个端点, 且区间长度在 $[d/2, d]$ 的信息的 $x$.

考虑我们询问所有 $r-l=d$ 的区间, 如果只能进行一次合并, 那么一定是对于某个 $m$ 合并 $[l, m]$ 和 $[m, r]$. 此时必然有 $m-l$ 和 $r-m$ 的一者不小于 $d/2$. 因此, $l,r$ 必有一者在 $S_{[d/2, d]}$ 中. 进一步, 我们可以得到 $S_{[d/2, d]}$ 中必须有 $\Omega(n)$ 个点, 那么长度在 $[d/2, d]$ 中的信息也必须有 $\Omega(n)$ 个被预处理了.

取一系列不交的 $[d/2, d]$, 我们可以取 $\Omega(\log n)$ 个, 这说明了被预处理的信息有 $\Omega(n\log n)$ 个.