自动搬运

查看原文

来自洛谷，原作者为

	Vsinger_洛天依 天如桜落月摇情 此方凡人入梦月 | 叫我小洛/依依/天依都可以哦 || 逆天依教（其实是粉丝群啦）：1009602220

搬运于2025-08-24 22:39:26，当前版本为作者最后更新于2024-09-12 19:09:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P8478 「GLR-R3」清明

参考了出题人题解和 xcyyyyyy 大神的题解，强推前两篇。

拿到题完全没思路怎么办？？？

人类智慧的巅峰，思维量的登峰造极。

换句话说就是非人题目，不过不得不说 GLR 的题是真的好，难度也是真的高。

首先我们需要看懂题面，这是第一个难点。

题面大意如下：

对于一个雨滴，它可以向任意编号小于等于 $\min\{i+k,n\}$ 的台阶上移动，而其对应的一部分容量也会在移动后修改至其移动后的台阶。

同时雨滴体积不会莫名其妙减少或者增多。

而在「下一个瞬间」其对应的奇妙度为 $\prod\limits_{i=1}^{n}a_i'$。

求所有本质不同的「下一个瞬间」的奇妙度总和。

考虑从数据范围入手。

• Subtask 5

  对于 $k=1$，在此情况下每个台阶上的雨滴最多只会向下移动一个台阶。

  我们定义 $c_i$ 为第 $i$ 个台阶向下一阶流动的雨水容量。

  那么我们就可以知道 $a_i'=a_i+c_{i-1}-c_i$。

  

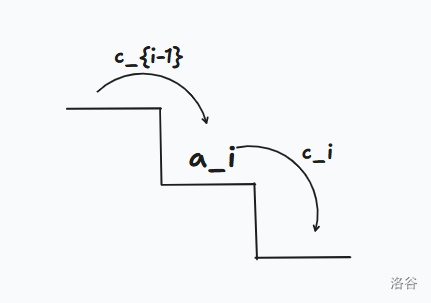
  可以发现 $ans=\sum\limits_{c}\prod\limits_{i=1}^{n}(a_i+c_{i-1}-c_i)$。

  考虑多项式展开，对于内部的 $a_i+c_{i-1}-c_i$ 我们直接划分为两部分：$a-c_i$ 和 $c_{i-1}$。

  此时我们推广到积就会得到很多项 $a-c_i$ 和 $c_{i-1}$ 的和，我们再引入一个子集 $S\subseteq\{1,2,3,\cdots,n\}$。

  每个 $i\in S$ 代表在 $a_i-c_i$ 中选取，否则代表在 $c_{i-1}$ 中选取。

  那么我们也就发现 $\prod\limits_{i=1}^{n}(a_i+c_{i-1}-c_i)=\sum\limits_{S\subseteq \{1,2,\cdots,n\}}\prod\limits_{i\in S} (a_i-c_{i})\prod\limits_{i\not\in S}c_{i-1}$。

  整体式子也就得到了 $ans=\sum\limits_{c}\sum\limits_{S\subseteq \{1,2,\cdots,n\}}\prod\limits_{i\in S} (a_i-c_{i})\prod\limits_{i\not\in S}c_{i-1}$。

  我们考虑去掉外层的 $\sum\limits_{c}$，策略就是把下标 $c_i$ 相同的一批都合成到一起。

  当 $i<n$ 时，考虑 $i$ 和 $i-1$ ，定义 $f_{i,1}$ 为包含 $i$ 的所有 $S$ 的乘积之和，$f_{i,1}$ 为不包含 $i$ 的所有 $S$ 的乘积之和，我们就可以分成 $4$ 个情况来转移。

  • $i - 1 \in S, i \in S$

    贡献是 $\sum\limits_{0\le c_i \le a_i}(a_i-c_i)=\frac{a_i(a_i+1)}{2}$。

  • $i - 1 \not \in S, i \in S$

    贡献是 $\sum\limits_{0\le c_i \le a_i} 1 = a_i+1$。

  • $i - 1 \in S, i \not \in S$

    贡献是 $\sum\limits_{0\le c_i \le a_i}(a_i-c_i)c_i = \frac{a_i^2(a_i+1)}{2}-\frac{a_i(a_i+1)(2a_i+1)}{6} = \frac{(a_i-1)a_i(a_i+1)}{6}$。

  • $i - 1 \not \in S, i \not \in S$

    贡献是 $\sum\limits_{0\le c_i \le a_i}c_i=\frac{a_i(a_i+1)}{2}$。

  那么我们就可以直接递推的从 $f_{i-1,0/1}$ 向 $f_{i,0/1}$ 转移。

  这样我们就终于完成了拿到了 13 pts，复杂度 $O(n)$。

• Subtask 6

  考虑从 Sub5 进行推广， $c_i \to c_{i,j}$ 代表第 $i$ 个台阶到第 $i+j$ 个台阶流动的量，然后就能拿到一个能拆的式子。

  $$\sum_{c}\prod_{i=1}^{n}\left(\sum_{j=0}^{\min(i-1,k)}c_{i-j,j}\right) $$

  然后再推好像就好点，我们继续展开。

  依然是先把 $\sum\limits_c$ 置之不理。

  我们设对于所有 $c_{i,j}$ 的出现下标构成的集合为 $S_i$，那么可以得到这样一个式子。

  $$\prod_{i=1}^n\prod_{j\in S_i}c_{i,j}$$

  考虑外层 $\sum_{c}$ 的影响，显然第一维不同的 $c$ 之间互不影响。

  先将外层乘积 $\prod_{i=1}^{n}$ 展开为若干 $n$ 次单项式的和，针对每个单项式，我们考虑 $c_{i,j}$ 的约束即 $\sum_j c_{i,j} = a_i$。

  利用乘法分配律，分别对每个 $i$ 维度的 $c_{i,j}$ 进行求和，最终我们可以收拢成一个和式。

  $$\prod_{i=1}^n\sum_{c_i}\left[\sum_{j}c_{i,j}=a_i\right]\prod_{j\in S_i}c_{i,j} $$

  这好像不是很好做啊，那我们可以构建一个组合意义来简化题面。

  我们用 $r_i$ 表示对于任意合法的 $j$，$c_{i,j}$ 中有 $r_i$ 个变量可以取到非 $0$ 值，也就是说 $r_i=\min(n-i,k)+1$。

  那么我们就可以建立这样的模型：

  有编号为 $0,1,2,\dots,r_i-1$ 的 $r_i$ 个盒子。

  其中编号落在属于 $S_i$ 的盒子，放了 $x$ 个球会贡献 $x$。

  而其它盒子无论放多少个球，贡献都是 $1$。

  一种方案的贡献为各个盒子的贡献的积。

  求往 $r_i$ 个盒子中任意放 $a_i$ 个没有任何区别的球的贡献之和。

  虽然还是不好做，但是起码可以构建生成函数了不是吗？

  我们可以发现我们并不关心 $S_i$ 具体是多少，我们只关心 $|S_i|$。

  我们构造生成函数来实现，对于编号在 $S_i$ 中的盒子，这些盒子的特点是放 $x$ 个球的贡献是 $x$，生成函数为 $\frac{x}{(1-x)^2}$，将球放进盒子时，贡献会随着球的数目成比例增加。

  剩下的盒子，这些盒子的特点是不论放多少球，贡献始终为 $1$，因此其生成函数为 $\frac{1}{1-x}$，球的数目对贡献无影响，但我们仍然允许球被放进去。

  将这些生成函数组合在一起，让 $|S_i| = s_i$，那么总生成函数为：

  $$G(x) = \left( \frac{x}{(1 - x)^2} \right)^{s_i} \cdot \left( \frac{1}{1 - x} \right)^{r_i - s_i} $$

  简化得到：

  $$G(x) = \frac{x^{s_i}}{(1 - x)^{s_i + r_i}}$$

  为了求往 $r_i$ 个盒子中放入 $a_i$ 个球的贡献，我们需要找到生成函数 $G(x)$ 中 $x^{a_i}$ 的系数：

  $$ [x^{a_i}] G(x) = [x^{a_i}] \frac{x^{s_i}}{(1 - x)^{s_i + r_i}} $$

  这等价于：

  $$[x^{a_i - s_i}] \frac{1}{(1 - x)^{s_i + r_i}}$$

  对 $\frac{1}{(1-x)^{s_i + r_i}}$ 展开，得到：

  $$\frac{1}{(1-x)^{s_i + r_i}} = \sum_{n=0} \binom{n + s_i + r_i - 1}{s_i + r_i - 1} x^n $$

  将这一展开式代入 $G(x)$ 中：

  $$\begin{aligned} G(x) &= x^{s_i} \sum_{n=0} \binom{n + s_i + r_i - 1}{s_i + r_i - 1} x^n\\ &= \sum_{n=0} \binom{n + s_i + r_i - 1}{s_i + r_i - 1} x^{n + s_i} \end{aligned} $$

  为了找到 $x^{a_i}$ 项，需要满足 $n + s_i = a_i$，可以得知 $n = a_i - s_i$。

  代入可以得到 $x^{a_i}$ 项的系数为：

  $$\binom{(a_i - s_i) + s_i + r_i - 1}{s_i + r_i - 1} = \binom{a_i + r_i - 1}{s_i + r_i - 1} $$

  可以发现结果只受到 $S_i$ 的影响，上面已经提到了，我们考虑 $s_i$ 是怎么来的。

  可以发现每个 $i$ 会向集合 $\max\{i-k,1\} \le j \le i$ 的某个盒子 $j$ 恰好贡献 $S_j$。

  因此每个 $i$ 在对应区间内，只会贡献一次。

  每个 $i$ 的贡献可以由多个位置 $j \in (i,i+k)$ 贡献，可以反过来理解：

  实际上每个 $s_i$ 可以从 $\{i, i+1, \dots, i+r_i-1\}$ 这些位置中任选一个贡献。

  进行 $dp$ 即可，设 $f_{i,j}$ 表示在后缀 $i$ 中有 $j$ 个位置没有贡献过 $s$ 的权值和。

  转移就枚举一下 $s$ 然后组合数计算，复杂度 $O(n^3)$

• Subtask 7

  拓展 Subtask 6 中的处理方法，考虑状压。

  设 $f_{i,S}$，用 $i$ 表示当前后缀，用 $S$ 表示 $i,i+1,i+2,\dots,\min(i+k,n)$ 是否已经都贡献过 $s$，复杂度 $O(n\cdot 3^k)$ 是过不去的。

  那咋办？注意到 $i$ 的贡献只和 $S$ 中新增的已经贡献过的位置个数有关，并且能贡献到 $S$ 的前驱状态 $T$ 得满足 $T\subseteq S$，因此我们可以直接做高维前缀和，同时记录一下新增个数即可。

  复杂度 $O(n\cdot k^2\cdot 2^k)$，可以通过 Subtask 7。

• Subtask 8

  直接莽 $O(n\cdot k^2\cdot 2^k)$！欸过不去，考虑优化。

  发扬人类智慧，我们发现在 $k$ 较大的时候只有较少的台阶会超出限制，大多数问题集中在一部分位置

  我们如果在 $k$ 和 $k+1$ 处对前后分成两部分的话，枚举后半段位置是否被前半段占用，从而使得前后的贡献分开计算。这样每一段的内部贡献就独立了

  因为前半段的贡献不会超出限制，因此每个内部后缀都可以贡献，问题转化为类似 Subtask 6 的形式

  考虑动态规划， $f_{i,j,S}$ 表示一下含义：

  • $i$: 从后缀 $i$ 开始。
  • $j$: 在区间 $[i, k]$ 中，尚未被占用的位置数。
  • $S$: 表示区间 $(k, n]$ 中的位置占用情况。

  然后根据前半段和后半段的不同情况分别处理。

  我们对前半段的 $j$ 做类似 Sub6 的转移，对 $S$ 做类似 Sub7 的转移。

  对于后半段，我们枚举 $S$ 来做类似 Sub6 的转移。

  复杂度为 $O(n\cdot k^2\cdot \sqrt k\cdot 2^k)$。

• Subtask 9

  Sub8 的做法又过不去了？

  我们引入容斥思想来优化 Sub8 的做法，为了优化算法，我们枚举后半段 $(k+1,n]$ 中的位置是否被超出限制占用。

  我们用状态 $f_{i,j}$ 来表示后缀 $i$ 中有 $j$ 个位置是可选的但未被占用

  在状态转移时，从 $f_{i+1}$ 转移到 $f_i$ 时，不仅要考虑位置 $i$ 是否被加入，还需要考虑位置 $i+k+1$ 是否被加入，和 Sub6 类似，但需要结合对后段的枚举。

  这样我们就解决了 Sub9，复杂度 $O(n^2\cdot k\cdot 2^{n-k})$。

现在我们解决了所有的 Subtask，我们将 Sub6，Sub7 和 Sub9 进行结合即可通过本题。