自动搬运

查看原文

来自洛谷，原作者为

	Reanap 你面向名为希望的绝望微笑。

搬运于2025-08-24 22:39:25，当前版本为作者最后更新于2022-03-24 23:18:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

同班化竞生 7min 切掉了，所以应该很简单。

一些吐槽：

为什么不用两个容器，为什么分隔板贴这么紧。

• Subtask 1

大户人家做法，每对溶液组配一个专用的！需要 $n^2$ 个， $26 \times 26 = 676 < 712$，可以通过。

• Subtask 2

第一个做法完全没有运用题目条件，即既没有拼板，也没有翻版，很不优。

现在我们节俭一点，每个溶液配一个板，一对溶液实验时两个板拼起来用。

要使用 $2 \times n$ 个板，可以通过 子任务 2。

• Subtask 3

第二个做法有明显缺陷，就是实验结束后，每个板都有一面是没有接触过溶液的，还是很浪费。

发现一个板如果只脏了一面，还可以换一面给其它溶液配上。

于是把 $X$ 溶液平均分为两组，我们只给第一组配一个专属板，$Y$ 仍然每个配一个专属板，然后把第一组的溶液拿去和 $Y$ 中的所有做实验，中间隔两块板。

然后把第一组的板翻个面作为第二组的专属板，然后去和 $Y$ 中做实验。

需要 $\lceil \frac{n}{2} \rceil + n$ 个板。

对于子任务3 发现多了一个板。

考虑再节约一点。当 $n$ 为奇数的时候，不对 $x_n$ 进行分组，重复上面步骤，但在第二组实验前，把 $x_n$ 和 $Y$ 中每一个实验了。

需要 $\lfloor \frac{n}{2} \rfloor + n$ 个板，恰能通过。

免责声明： 数据点是 Rainybunny 安排的，如果有同学对这组子任务卡了向上向下取整的行为心怀不满，可以和她深入交流一下，与我无关。

• Subtask 4

分析一下做法 3 的劣势。最劣的地方是，我们用板的脏面去触碰了板的干净面，这种行为我们认为是极其不优秀的，我们带着这种想法去构造更优方案。

我们把 $X$ 均分为 3 组，但同时，我们也把 $Y$ 均分为 3 组，$Y$ 每个配一个板，$X$ 第一组每个配一个板。

把 $X$ 的第一组先与 $Y$ 反应。如图：（竖线表示一组板，波浪线表示该组板的该面是有溶液的）

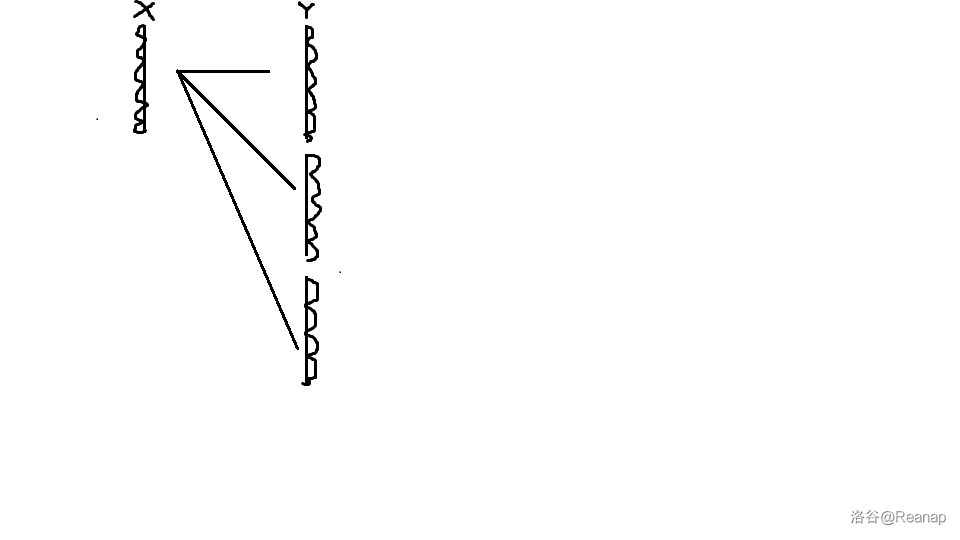
然后把 $Y$ 的第三组拿给 $X$ 的第二组，然后进行如下的实验：

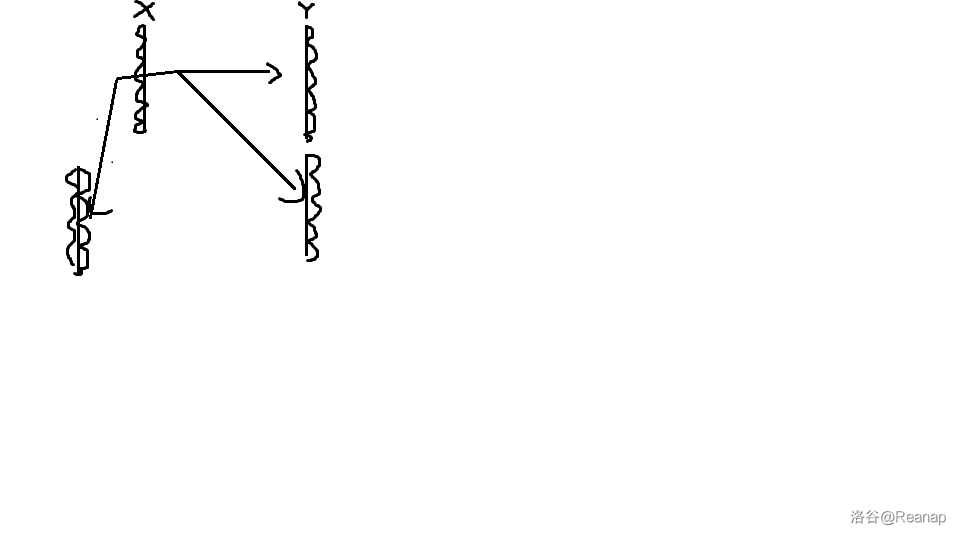
注意到现在 $Y$ 配的板的左面依然干净，把 $Y$ 第二组的板给 $X$ 的第三组，然后进行类似上面的实验：

最后，把 $X$ 第一组给 $Y$ 第二组，$Y$ 第一组翻面给 $Y$ 的第三组，然后剩下随便配就是了。

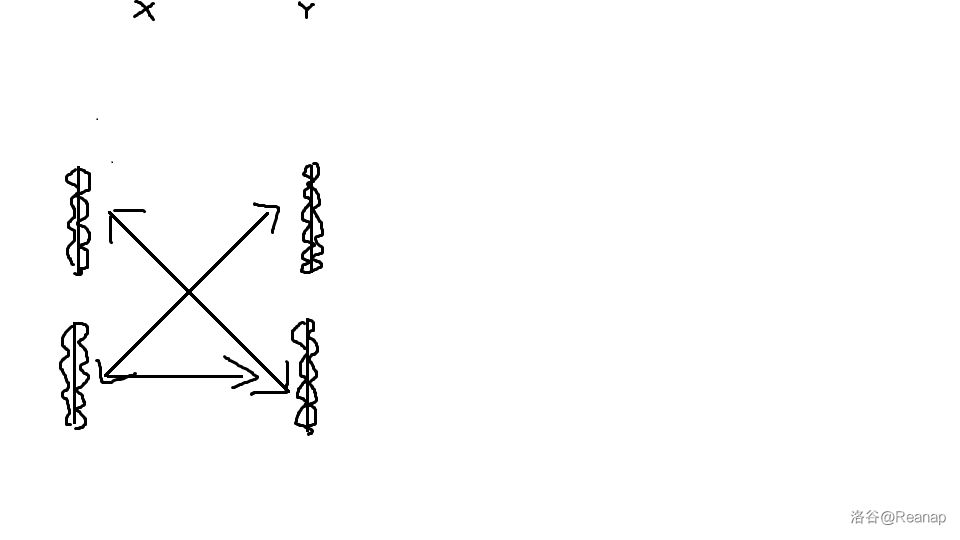
说完了。要用 $\frac{n}{3} + n$ 个板。

这个子任务没有卡边界情况啥的。

• Subtask 5

发现上个做法有一个很糟心的点，就是我们在进行三层板操作时，我们用了一大片右面干净板来保证 $Y$ 的板的左面是干净的，但简单思考，发现我们只需要额外申请一个板就可做成这件事，而不用保证那么多的板右面随时干净。

因此继续，我们把 $X$ 分为四组，第一组配板， $Y$ 分为四组，每个配板。

先把 $X$ 第一组与 $Y$ 每一个实验一次，然后把 $X$ 第一组反过来给第二组，然后申请一个额外板，隔三层板把第二组板与 $Y$ 中溶液做实验。

得到如下局面($Y$ 板左面依然干净)：

把 $Y$ 第三组第四组的给 $X$ 第三组第四组的，然后继续用额外板隔三层板做实验：

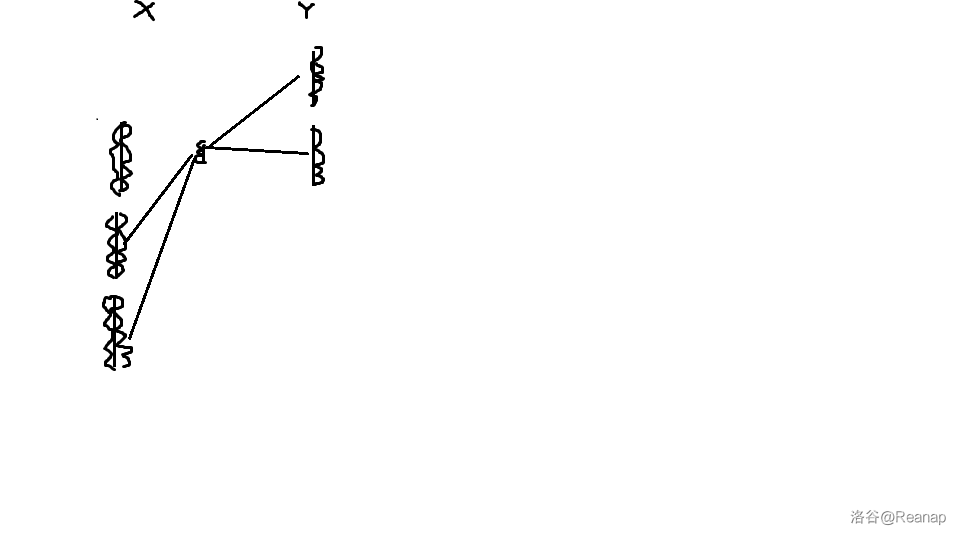
然后把 $Y$ 第一二组的反过来给三四组，随便实验一下就结束了：

使用了 $\frac{n}{4} + n$ 块板。

• Subtask 7

我们在上面全部的做法中，我们全部给 $Y$ 做了满配，只给了一部分 $X$ 分了板子。

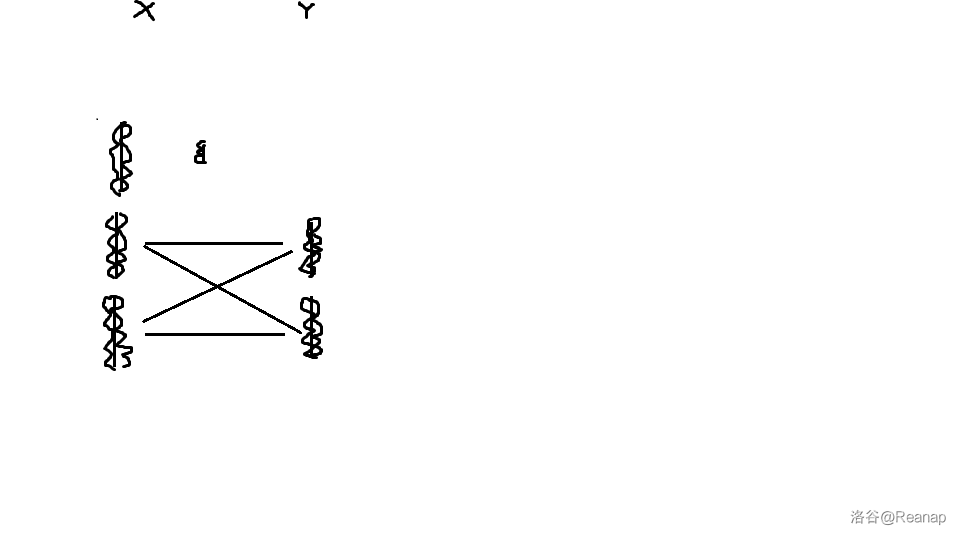
考虑这样一种构造，我们把 $X$ 平均分为两组，$Y$ 平均分为三组。$X$ 中一组配板，$Y$ 中两组配板 , 然后先进行一部分实验。

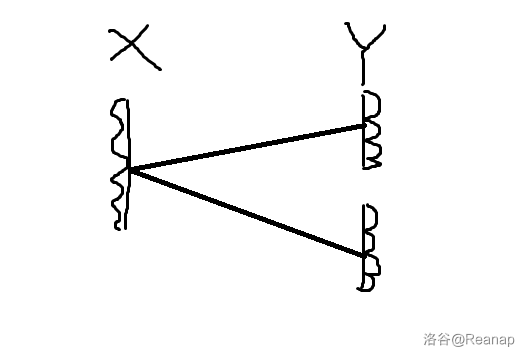
然后添加一个神奇的板，把 $Y$ 中第一组的板翻面放到第三组，然后隔着神奇的板再进行实验。

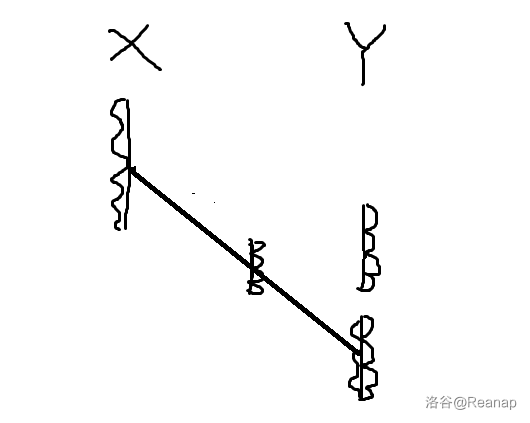
之后把 $X$ 中第一组的板翻面给第二组，通过翻面的神奇的板再实验一轮。

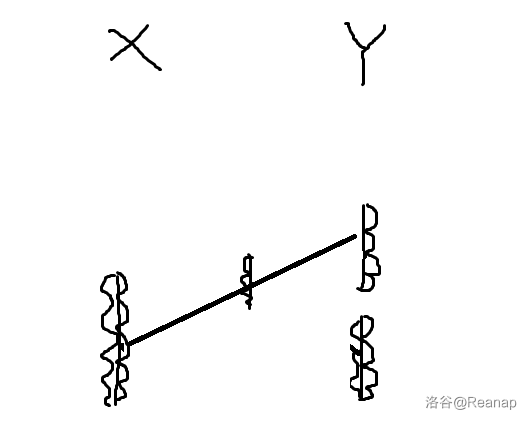
最后把 $Y$ 中第二组的翻面给第一组做一轮实验就好了。

于是，我们使用了 $\frac{n}{2}+\frac{2n}{3} = \frac{7n}{6}$ 块板，可以通过本题。

/*+Rainybunny+*/

#include <bits/stdc++.h>

#define rep(i, l, r) for (int i = l, rep##i = r; i <= rep##i; ++i)
#define per(i, r, l) for (int i = r, per##i = l; i >= per##i; --i)

int main() {
    int n; scanf("%d", &n);
    int s0 = n + 1 >> 1, t0 = (n + 2) / 3, t1 = (n - t0 + 1) >> 1;
    int p = s0 + t0 + t1 + 1;

    printf("%d\n", p);
    rep (i, 1, s0) { // S0->T0, S0->T1.
        rep (j, 1, t0 + t1) {
            printf("2 %d %d %d %d\n", i, i, j + s0, j);
        }
    }
    rep (i, 1, s0) { // S0->T2.
        rep (j, t0 + t1 + 1, n) {
            printf("3 %d %d %d %d %d\n", i, i, p, -(j - t1 + s0), j);
        }
    }
    rep (i, s0 + 1, n) { // S1->T0.
        rep (j, 1, t0) {
            printf("3 %d %d %d %d %d\n", i, -(i - s0), -p, j + s0, j);
        }
    }
    rep (i, s0 + 1, n) { // S1->T1.
        rep (j, t0 + 1, t0 + t1) {
            printf("2 %d %d %d %d\n", i, -(i - s0), -(j - t0 + s0), j);
        }
    }
    rep (i, s0 + 1, n) { // S1->T2.
        rep (j, t0 + t1 + 1, n) {
            printf("2 %d %d %d %d\n", i, -(i - s0), -(j - t1 + s0), j);
        }
    }
    return 0;
}