自动搬运

查看原文

来自洛谷，原作者为

	LinkyChristian 公式恐惧症一级患者||Linky~Linky~Lin||关注Linky，场场AK！||Revue ☆ Starlight

搬运于2025-08-24 22:39:18，当前版本为作者最后更新于2022-01-09 17:19:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

【题解】调整圣剑

首先，这是个最小割模型。

建分层图，一共 $k$ 层，每层 $n+1$ 个点 ， $n$ 条边，第 $i$ 条边的权值为 $a_i$ ，割掉这条边表示这次选择了第 $i$ 个护符。

考虑限制，对于限制 $(i,j,x,y)$ 我们从第 $i$ 层的第 $x+1$ 个点向第 $j$ 层的第 $n-y+1$ 个点连一条权值为 $INF$ 的边，这样如果第 $i$ 层不割掉前 $x$ 条边中的一条且第 $j$ 层不割掉后 $y$ 条边中的一条，就会出现一条路径，不符合最小割定义。

最后从源点向每一层的第一个点连 $INF$ 边，从每一层的最后一个点向汇点连 $INF$ 的边，就可以跑 $MaxFlow-MinCut$ 了。

那么有了这两点思路后，我们可以把样例 $1$ 的图建出来。

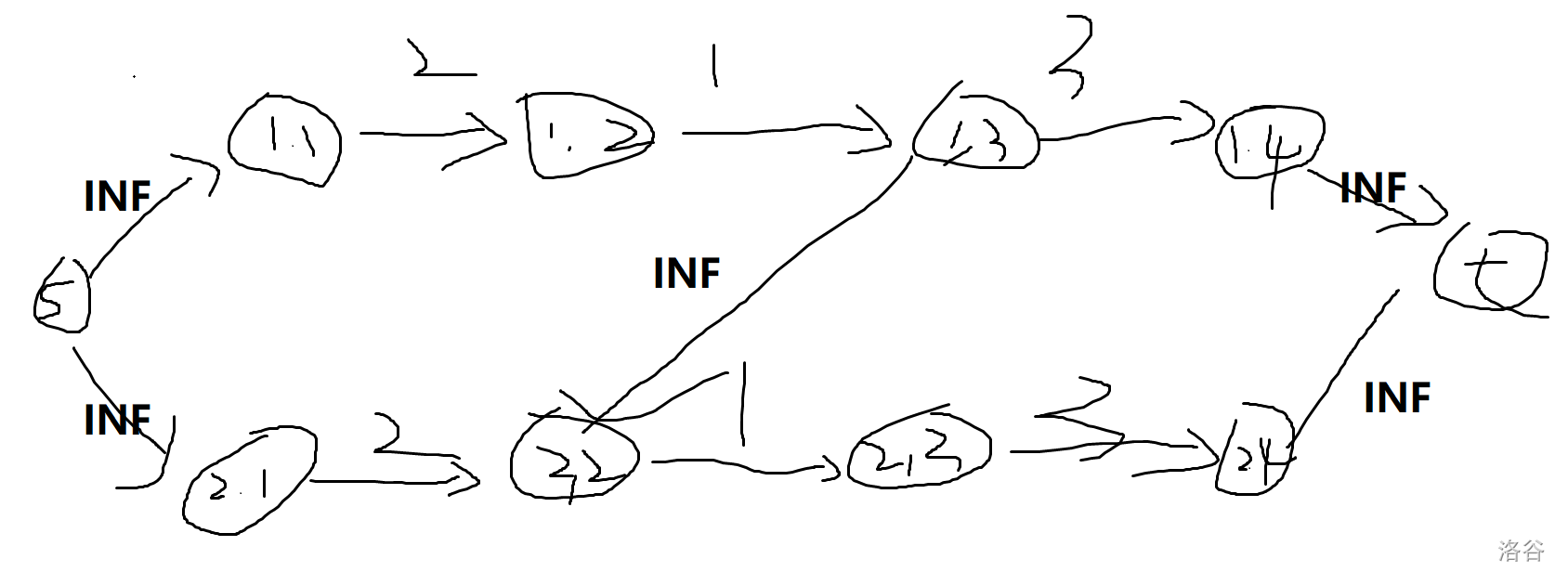
但是发现以 $n \le 10^5$ ， $k,q \le 10^4$ 的数据量， $n \times k$ 个点连建都建不出来。

怎么优化呢？从最大流的角度思考。我们发现原图里有很多长长的链。

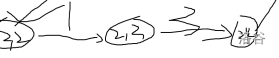
这些链代表了 $1-n$ 中的一些区间。对于这些只能向一个方向流的链，我们显然可以将这些链缩成边，边的容量为这些链流量中的最小值。由于是区间最小值，用 $RMQ$ 即可。

到了这一步还没有结束。

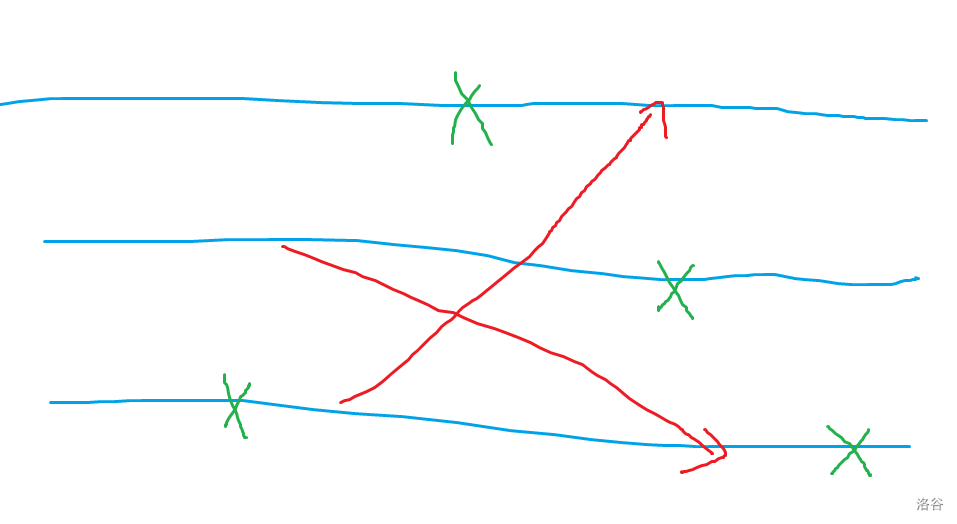
有时候会出现这样的情况，导致一次选择选取了两个护符，因此我们需要把每一条边加上一个大数（如 $10^{10}$），使得割 $k+1$ 条边的情况严格劣于割 $k$ 条边的情况。

于是我们获得了最终的建图方式，以下是样例 $3$ 的建图。

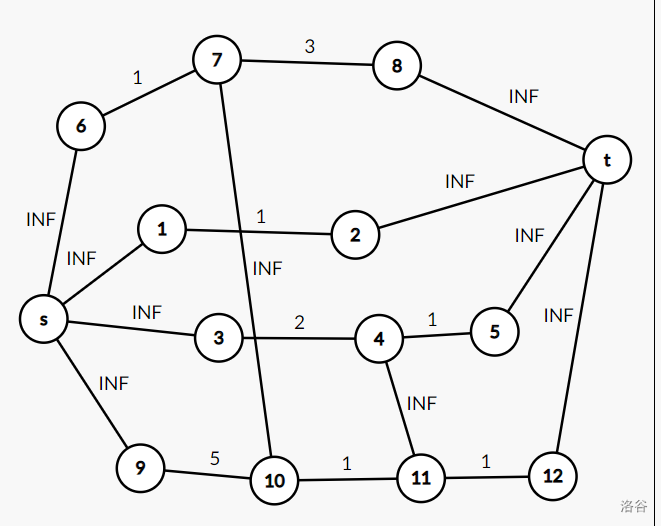
分析一下复杂度：一开始有 $k$ 条边，每加一个限制会多出 $2$ 个点和 $3$ 条边，边和点的数量级都和 $k,q$ 相同（即 $10^4$） ，跑 $Dinic$ 可以通过，当然要是你觉得这个理论复杂度不符的话，可以换更快的网络流算法。

附上 $std$

#include<bits/stdc++.h>
#define N 40010
#define M 500010
#define mk make_pair
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
namespace MaxFlow{
	int cnt=1,head[N],cur[N],dep[N],to[M],nxt[M];
	ll val[M],INF=1e14;
	void insert(int u,int v,ll w){
		cnt++;
		to[cnt]=v;
		val[cnt]=w;
		nxt[cnt]=head[u];
		head[u]=cnt;
	}
	void ins(int u,int v,ll w) {
		insert(u,v,w);
		insert(v,u,0);
	}
	bool bfs(int ss,int tt) {
		queue<int> q;
	    memset(dep,0,sizeof(dep));
	    q.push(ss),dep[ss]=1;
	    while(!q.empty()) {
	    	int now=q.front();q.pop();
	    	for(int i=head[now]; i; i=nxt[i]) 
	    	    if(val[i]&&!dep[to[i]]) {
	    	    	dep[to[i]]=dep[now]+1;
	    	    	q.push(to[i]);
	    	    }
	    }
	    return dep[tt]!=0;
	}
    ll dfs(int now,ll dis,int tt) {
    	if(now==tt) return dis;
    	ll res=0;
    	for(int& i=cur[now]; i; i=nxt[i])
    	    if(val[i]&&dep[to[i]]==dep[now]+1) {
    	    	ll tmp=dfs(to[i],min(dis-res,val[i]),tt);
    	    	res+=tmp,val[i]-=tmp,val[i^1]+=tmp;
    	    	if(res==dis) return res;
    	    }
    	if(!res) dep[now]=-1;
    	return res;
    }
	ll Dinic(int ss,int tt) {
        ll res=0;
        while(bfs(ss,tt)) {
        	memcpy(cur,head,sizeof(head));
        	while(ll tmp=dfs(ss,INF,tt)) res+=tmp;
        }
        return res;		
	}
}
inline ll read() {
	ll res=0,f=1;char ch=getchar();
	while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
	while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
	return f*res;
}
using namespace MaxFlow; 
vector<int> cut[M];//分割点 
int n,k,q,a[M],mn[M][22],lg[M];
int RMQ(int l,int r) { 
	int lg2=lg[r-l+1]; 
	return min(mn[l][lg2],mn[r-(1<<lg2)+1][lg2]);
}
int tot,s,t;
map<pii,int> mp;
pii b1[M],b2[M];
int main()
{
	n=read(),k=read(),q=read();s=0,t=40000;
	for(int i=2; i<=n; i++) lg[i]=lg[i/2]+1;
	for(int i=1; i<=n; i++) a[i]=mn[i][0]=read();
	for(int d=1; d<=q; d++) {
		int i=read(),j=read(),x=read(),y=read();
		if(x==n||y==n) continue;//特判，如果x或y为n表示其中一个选了任意一个都满足条件，相当于没有条件 
		cut[i].push_back(x),cut[j].push_back(n-y);
		b1[d]=mk(i,x),b2[d]=mk(j,n-y);
	}
	for(int i=1; i<=n; i++) sort(cut[i].begin(),cut[i].end());
	for(int d=1; d<20; d++)//RMQ
	    for(int i=1; i+(1<<d)-1<=n; i++) mn[i][d]=min(mn[i][d-1],mn[i+(1<<(d-1))][d-1]);
	for(int i=1; i<=k; i++) {
		cut[i].push_back(n);//最后一段即使没有也得缩 
		int now=0,nid=++tot;
		ins(s,nid,INF);
		for(int j=0; j<cut[i].size(); j++) 
			if(!j||(j>0&&cut[i][j]!=cut[i][j-1]))//有可能有重复点 
			    ins(nid,++tot,RMQ(now+1,cut[i][j])+1e10),//防止一条边选多次 
				now=cut[i][j],nid=tot,mp[mk(i,cut[i][j])]=tot;
		ins(nid,t,INF);
	} 
	for(int i=1; i<=q; i++) ins(mp[b1[i]],mp[b2[i]],INF);
	ll ans=Dinic(s,t)-k*1e10;
	printf("%lld",ans);
    return 0;
}