自动搬运

查看原文

来自洛谷，原作者为

	Shanganze **

搬运于2025-08-24 22:39:04，当前版本为作者最后更新于2023-06-27 20:19:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先简化题意：

每一棵基环树上以其编号最小的点作为根，求要使至少 $k$ 个点不与任意一个根联通最少需要删几条边。

首先考虑如果是一棵正常的树，最优方案就是删除根节点和它儿子的边，那么该儿子所在子树所有节点都与根节点不连通。可以看为一个费用为 $1$ 的物品，价值为该子树大小。

那么转移到基环树上来看，基环树就是比普通树多一条边。

分类讨论：

1. 这条边所连接的两点在两个子树内，如果要获取其中一个子树的价值，就必须把这两个子树的与根的链接都断开。也就是把两个费用 $1$ 物品合并成一个费用 $2$ 物品，价值为两子树大小和。

2. 这条边所连接的两点在同一个子树内，显然不影响正常的答案（这是 $A$ 了之后才想到的）。

但是看下面这张图

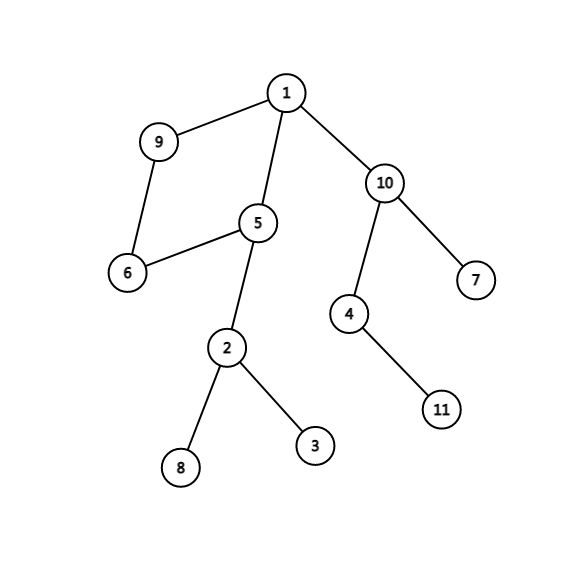
如果 $k=7$ 时，按上面的考虑断开 $1-9$ $$ $1-10$ $$ $1-5$ 的三条边，但是显然可以断开 $1-10$ $$ $5-2$ 的两条边。

由此我们考虑到可以，我们还有一种选择：断开这个环上的一点向外的链接（不能是根），费用为 $1$，价值为相连那一点的子树大小。而且可以看出一个环上，最多只会断开一次对外的链接（如果断开两次，那么价值显然不如直接断开和根的链接）。所以我们只需要找出这个环上断开一条向外链接最大的价值。

我们再考虑统计答案。通过上面的分析，我们已经将转化为一个子问题，有若干个费用为 $1$ 的物品，还有若干费用为 $2$ 的物品，每一个费用 $2$ 物品与一个费用 $1$ 物品相对应（也就是这两个物品中只能选一个）。

考虑贪心。

若单独费用为 $1$ 的物品选了 $x$ 个，一定是前 $x$ 大，这个很简单。

记绑定的物品费用 $1$ 的价值为 $a$，费用 $2$ 的价值为 $b$，分以下两类情况。

$2a \gt b$，这部分可以把费用 $2$ 价值 $b$ 的物品拆成费用 $1$ 价值 $b-a$ 的物品，然后和单独费用 $1$ 的物品放一起简单贪心，不赘述了。

$2a \le b$，把所有 $2a \le b$ 的分成一组，可以断言最多只会选一个费用 $1$ 的物品。

证明很简单，假设选了 $a_1,a_2$，不妨设 $a_1\le a_2$，那么 $a_1,a_2$ 替换为 $b_2$ 更优，因为 $b_2 \ge 2a_2 \ge a_1+a_2$。

这一组按 $b$ 降序排序后只有三种情况。选了一个前缀的费用 $2$，或者前缀里面刨去了一个 $b-a$ 最小的选费用 $1$，或者后缀里面选了一个 $a$ 最大的费用 $1$，总之可以枚举前缀，然后二分查找前面贪心的部分即可。

总复杂度 $O(n\log n)$。

贪心部分鸣谢 Rosaya

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
int n,m,v[N],z[N],siz[N],ans1[N],cnt1,cnt2,ans=1e9,cnt3;
struct a3{
	int a,b,c;
}ans2[N],ans3[N];
bool a33(a3 a,a3 b){return a.b>b.b;}
struct a1{int nex,to;}x[N<<1];
int head[N],p,k,f[N],t[N],maxx[N];
bool a2(int a,int b){return a>b;}
int find(int a){
	if(f[a]==a)return a;
	return f[a]=find(f[a]);
}
void add(int a,int b){
	x[++p].to=b;
	x[p].nex=head[a];
	head[a]=p;
}
void dfs(int a,int fa,int p){
	v[a]=1;siz[a]=1;
	for(int q=head[a];q;q=x[q].nex){
		int o=x[q].to;
		if(o!=fa){
			dfs(o,a,p);
			z[a]^=z[o];siz[a]+=siz[o];//想一下为什么用异或
		}
	}
	if(a==p)return;
	for(int q=head[a];q;q=x[q].nex){
		int o=x[q].to;
		if(o!=fa){
			if(z[o]==0){
				t[z[a]]=max(t[z[a]],siz[o]);
			}
		}
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin>>n>>k;
	for(int q=1;q<=n;q++)f[q]=q;
	for(int q=1;q<=n;q++){
		int a,b;
		cin>>a>>b;
		if(find(a)==find(b)){
			z[a]=z[b]=++cnt2;
			continue;
		}
		add(a,b);add(b,a);
		f[find(a)]=f[find(b)];
	}	
	for(int q=1;q<=n;q++){
		if(v[q]==0){
			dfs(q,q,q);
			for(int i=head[q];i;i=x[i].nex){
				int o=x[i].to;
				if(z[o]==0)ans1[++cnt1]=siz[o];
				else ans2[z[o]].b+=siz[o],ans2[z[o]].a=t[z[o]];
			}
		}
	}
	for(int q=1;q<=cnt2;q++){
		if(ans2[q].a*2>=ans2[q].b){
			ans1[++cnt1]=ans2[q].a;
			ans1[++cnt1]=ans2[q].b-ans2[q].a;
		}
		else{
			ans3[++cnt3]=ans2[q];
		}
	}
	sort(ans1+1,ans1+1+cnt1,a2);sort(ans3+1,ans3+1+cnt3,a33);
	for(int q=1;q<=cnt1;q++)ans1[q]+=ans1[q-1];
	for(int q=cnt3;q>=1;q--){ans3[q].c=max(ans3[q+1].c,ans3[q].a);}
	for(int q=1;q<=cnt3;q++){ans3[q].a=ans3[q].b-ans3[q].a;ans3[q].b+=ans3[q-1].b;}
	int o=1e9;
	for(int q=0;q<=cnt3;q++){
		o=min(ans3[q].a,o);
		int p=ans3[q].b,u=q*2;
		if(p>=k){
			ans=min(u,ans);continue;
		}
		if(ans1[cnt1]<k-p-ans3[q+1].a)continue;
		int w=lower_bound(ans1+1,ans1+1+cnt1,k-p-ans3[q+1].a)-ans1+1;ans=min(ans,u+w+1);
		if(ans1[cnt1]<k-p)continue;
		int i=lower_bound(ans1+1,ans1+1+cnt1,k-p)-ans1+1;ans=min(ans,u+i);
		if(ans1[cnt1]<k-p+o)continue;
		int j=lower_bound(ans1+1,ans1+1+cnt1,k-p+o)-ans1+1;ans=min(ans,u-1+j);	
	}
	cout<<ans;
	return 0;
}

代码不懂可以私信我。