自动搬运

查看原文

来自洛谷，原作者为

	LPF 看不懂黑白却听得到钟摆，去新世界冒险和内心作伴

搬运于2025-08-24 22:38:57，当前版本为作者最后更新于2022-08-19 15:35:18，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目链接

• 给定无向图，判断是否有 $1\to n$ 且长度不等于最短路的简单路径。
• $n\leq 10^5,m\leq 2\times 10^5$。

根据部分分大力得到正解，一步步来。

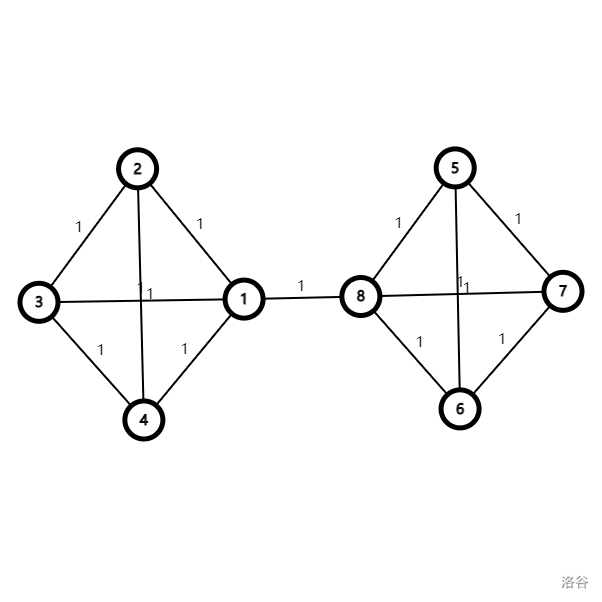
首先对于 $m\leq 40$ 可以搜索出所有路径，$n\leq 18$ 直接状压，那么目光聚集于 $m-n\leq 13$。

不难条件反射出广义串并联图方法（广告：广义串并联图方法学习笔记），缩合后得到 $m\leq 3\times 13$ 同样可以搜索做，当然这一方法的作用不止于此。

首先先描述一下具体的缩合方法：

• 一度点就直接删，二度点的边权就直接相加。
• 叠合重边则需要注意：
  • 如果重边的边权不同则将边权设置为不可到达，比如 $-1$（因为路径上显然不能包含这两个重边）。
  • 否则就还是原权值。
• 同时还有特殊的一点，就是 $1,n$ 即使度数 $\leq 2$ 也不作为缩合对象。

自行想象一下 no 的情况，大概就是所有 $1\to n$ 的简单路径们都缩到了 $(1,n)$ 这唯一一条边上，且边权不为 $-1$。

于是大胆断言答案为 no 当且仅当：缩合后 $s$ 的唯一出边是 $(s,t,w)$，且 $w\neq -1$。

当然这个猜测随便 hack，比如 Froggy 在 LOJ 讨论 里提到的 hack 长这样：

虽然这个 hack 看上去有些取巧，但是至少是个 hack，而且变相的更加使我们相信这个不靠谱的猜想有一定正确性。

再看一眼部分分，发现有：对于任意三座不同的城市 a, b, c，均存在一条从城市 $a$ 到城市 $c$ 且不经过城市 $b$ 的路径 这个 sub。

翻译成人话就是整个图形成一个点双，同时不难发现上述 hack 的思路就是存在不同时包含 $1$ 和 $n$ 的点双。

那么难道说如果整张图是一个点双上述猜想就正确吗，实际上是这样的，证明如下：

此处证明参考官方题解并结合自己的一点思考，可以看作是本题最核心部分之一。

首先整理一下已知条件：整个图是点双联通的且所有点的度数 $\geq 3$。同时有点数 $n\geq 4$，否则无法满足度数均 $\geq 3$ 的限制。

考虑将所有边定向，根据从 $1$ 到它们的最短路，与最短路扩展方向同向定向。

如果此时就有 $(u,v,w)$ 使得 $\text{dis}(1,u)+w+\text{dis}(v,n)\neq \text{dis}(1,n)$ 的话那肯定是没救了。

否则定向后，称入度 $>$ 出度的点为红色点，否则称为蓝色点。

然后考虑 $1\to n$ 的经过节点个数最多的简单路径，$1\to a_1\to a_2\to \cdots\to a_p\to n$。

首先得到 $a_1$ 入度一定是 $1$，$a_p$ 的出度一定是 $1$，否则一定能找到经过点数更多的路径。

同时由于任意点度数 $\geq 3$，所以 $a_1$ 一定是蓝色的，$a_p$ 一定是红色的，换言之，路径一定经历了蓝红替换的过程。

考虑找到这样一条边，使得 $a_i=u,a_{i+1}=v$，且 $u$ 为蓝色，$v$ 为红色。

根据定义，一定存在 $u\to x(x\neq v)$ 以及 $y\to v(y\neq u)$，此时考虑路径 $1\to y\to v\to u\to x\to n$。

除了 $v\to u$ 之外，所有边任然需要根据定向移动。

如果它不是简单路径，不难发现只有可能是 $x\to n$ 与 $1\to y\to v$ 这段路径上有重合，不妨设第一个重合点为 $x'$。

那么将原路径替换为 $1\to u\to x\to z\to y\to v\to n$ 是经过更多点的选择，不符合定义。

所以这条路径一定是简单的，且 $>$ 最短路径的。证毕。

如此，所有非正解的部分分都有了解决方法。

当然更进一步也是容易的，因为如果从 $1$ 出发进入一个以 $1$ 为割点且不包含 $n$ 的点双肯定是没有简单路径能到 $n$ 的。

所以直接加一条 $(1,n,\text{dis}(1,n))$ 即等于它们之间最短路径的边，然后只考虑同时包含 $1,n$ 的这个点双即可。

复杂度 $O(m\log m)$。

#include<bits/stdc++.h>
typedef long long ll;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define Ede(i, u) for(int i = head[u]; i; i = e[i].nxt)
using namespace std;

#define eb emplace_back
typedef pair<int, ll> pii;
#define mp make_pair
#define fi first
#define se second

inline int read() {
	int x = 0, f = 1; char c = getchar();
	while(c < '0' || c > '9') f = (c == '-') ? - 1 : 1, c = getchar();
	while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
	return x * f;
}

const int N = 1e5 + 10;
const ll inf = 1e16;
int n, m;

unordered_map<int, ll> g[N];

void add(int u, int v, ll w) {
	if(g[u].find(v) != g[u].end()) {
		if(g[u][v] != w) g[u][v] = g[v][u] = -1;
	}
	else g[u][v] = g[v][u] = w;
}


ll dis[N]; bool vis[N];
vector<pii> h[N];

ll getdis() {
	priority_queue<pair<ll, int> > q;
	rep(i, 1, n) dis[i] = inf;
	dis[1] = 0, q.push(mp(0, 1));
	while(! q.empty()) {
		int u = q.top().se; q.pop();
		if(vis[u]) continue;
		vis[u] = true;
		for(auto e : h[u]) {
			int v = e.fi; ll w = e.se;
			if(dis[v] > dis[u] + w)
				dis[v] = dis[u] + w, q.push(mp(- dis[v], v));
		}
	}
	return dis[n];
}

int dfn[N], low[N], stk[N], top, tim, cnt;
vector<int> scc[N];

void dfs(int u) {
	dfn[u] = low[u] = ++ tim;
	stk[++ top] = u;
	for(auto e : h[u]) {
		int v = e.fi;
		if(! dfn[v]) {
			dfs(v), low[u] = min(low[u], low[v]);
			if(low[v] == dfn[u]) {
				int o = 0; cnt ++;
				do {o = stk[top --], scc[cnt].eb(o);} while(o != v);
				scc[cnt].eb(u);
			}
		}
		else low[u] = min(low[u], dfn[v]);
	}
}

bool valid[N];

void build() {
	n = read(), m = read();
	rep(i, 1, m) {
		int u = read(), v = read(), w = read();
		h[u].eb(mp(v, w));
		h[v].eb(mp(u, w));
	}
	ll cur = getdis();
	h[1].eb(mp(n, cur));
	h[n].eb(mp(1, cur));
	dfs(1);
	rep(i, 1, n) vis[i] = false;
	int pos = 0;
	rep(i, 1, cnt) {
		for(int o : scc[i]) vis[o] = true;
		if(vis[1] && vis[n]) {pos = i; break;}
		for(int o : scc[i]) vis[o] = false;
	}
	assert(pos);
	for(int o : scc[pos]) valid[o] = true;
	rep(u, 1, n) if(valid[u])
	for(auto e : h[u]) if(valid[e.fi]) add(u, e.fi, e.se);
}

queue<int> q;
void push(int u) {if(u != 1 && u != n && (int) g[u].size() <= 2) q.push(u);}

int main() {
	build();
	rep(i, 1, n) push(i);
	while(! q.empty()) {
		int u = q.front(); q.pop();
		if(g[u].empty()) continue;
		for(auto o : g[u]) g[o.fi].erase(u);
		if((int) g[u].size() == 2) {
			auto cur = g[u].begin();
			int x = cur -> fi; ll a = cur -> se; cur ++;
			int y = cur -> fi; ll b = cur -> se;
			ll w = (a == -1 || b == -1) ? -1 : a + b;
			add(x, y, w);
		}
		for(auto o : g[u]) push(o.fi);
		g[u].clear();
	}
	if(g[1].find(n) != g[1].end() && g[1][n] != -1 && (int) g[1].size() == 1) puts("0"); else puts("1");
	return 0;
}