自动搬运

查看原文

来自洛谷，原作者为

	David_Mercury The love you take is equal to the love you make.

搬运于2025-08-24 22:38:46，当前版本为作者最后更新于2022-11-03 17:21:08，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意简述

自己看

题目分析

这道题的核心思想就是枚举。

55pts 解法：

使用前缀和储存地图树的棵数，去二分枚举水池的边长，然后去枚举所有可能的左上角位置，检验是否合法即可。

100pts 解法：

可以发现，树是非常稀疏的，最多仅为 $100$ 棵。因此就想：是否可以通过枚举树来枚举正方形。

很明显的，正方形的上、下、左、右界限，会被树或者墙所限制。而此时它的边长，就为上下界距离、左右界距离中更小的那一个。而代表上下界的树一定在两棵左右界树之间。因此，基本的枚举思路，就是将树从左到右进行排序，接着枚举所有可能的左右界。在每一次从左界开始往右枚举右界时，就可以顺便求出中间的上下界。

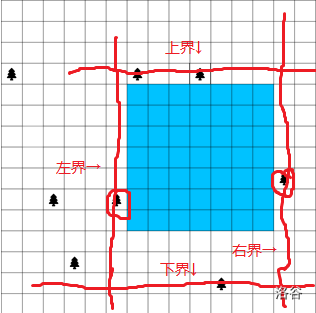
而上下界树的具体确定方式，相当于以左界树为中轴，取一路上找过去，离这个“中轴”最近的树，就像向中间压缩过去一样。

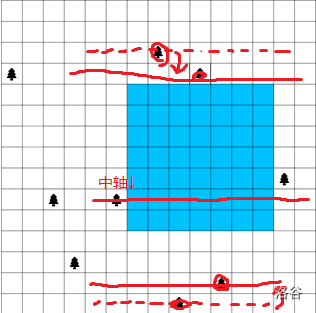
这一段的代码大概如下：

sort(tree+1, tree+1+t, cmp1);
int ans = 0;
for(int i=1; i<=t; i++){
    int minn = 1, maxn = n;										//上下界在初始时为墙 
    for(int j=i+1; j<=t; j++){
        if(maxn-minn-1 < tree[j].x-tree[i].x-1) break;          //如果上下界距离小于左右界距离，无继续枚举必要 
        ans = max(ans, tree[j].x-tree[i].x-1);                  //检测边长 
        if(tree[j].y<=tree[i].y) minn = max(minn, tree[j].y);   //打擂台，求上下界 
        if(tree[j].y>=tree[i].y) maxn = min(maxn, tree[j].y);
    }
}

现在你可以开心地发现我们已经过了第二个样例，也就是没有墙 / 上界或下界为墙 / 上界与下界为墙的情况。但是，还有一些有靠墙的特殊情况我们还没有处理。

1. 四界为墙

显然在有树的情况下就不存在。

2. 有相邻两界 / 三界为墙

这便是样例一的情形。

可以证明，此时的最优正方形必有一个角是靠在墙上的。所以我们只需要在地图的四个角上种树，即可将这种情况转化为全是树的情况。

3. 有左界或右界 / 左界与右界为墙

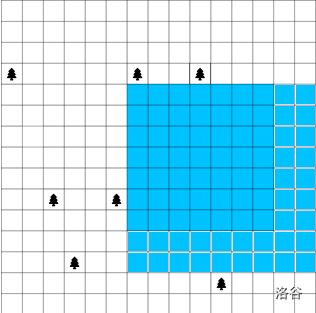
这种情况，我们只需要以上下顺序排序，并以枚举上下界的方式走一遍我们之前的枚举左右界的程序即可。

完整代码

#include<bits/stdc++.h>
using namespace std;

const int MAXT = 105;
int n, t;
struct node{
	int x, y;
} tree[MAXT];

bool cmp1(node a, node b){
	return a.x < b.x;
}

bool cmp2(node a, node b){
	return a.y < b.y;
}

int main(){
	scanf("%d%d", &n, &t);
	n++;
	for(int i=1; i<=t; i++) scanf("%d%d", &tree[i].x, &tree[i].y);
	//四角种树 
	tree[++t] = {0,0}, tree[++t] = {0,n};
	tree[++t] = {n,n}, tree[++t] = {n,0};
	//枚举左右界 
	sort(tree+1, tree+1+t, cmp1);
	int ans = 0;
	for(int i=1; i<=t; i++){
		int minn = 1, maxn = n;
		for(int j=i+1; j<=t; j++){
			if(maxn-minn-1 < tree[j].x-tree[i].x-1) break;
			ans = max(ans, tree[j].x-tree[i].x-1);
			if(tree[j].y<=tree[i].y) minn = max(minn, tree[j].y);
			if(tree[j].y>=tree[i].y) maxn = min(maxn, tree[j].y);
		}
	}
	//枚举上下界 
	sort(tree+1, tree+1+t, cmp2);
	for(int i=1; i<=t; i++){
		int minn = 1, maxn = n;
		for(int j=i+1; j<=t; j++){
			if(maxn-minn-1 < tree[j].y-tree[i].y-1) break;
			ans = max(ans, tree[j].y-tree[i].y-1);
			if(tree[j].x<=tree[i].x) minn = max(minn, tree[j].x);
			if(tree[j].x>=tree[i].x) maxn = min(maxn, tree[j].x);
		}
	}
	cout<<ans;
	
	return 0;
}

废话后记

第一次写题解，可能有疏漏，欢迎指出。

最后的最后，感谢您的观看！