自动搬运

查看原文

来自洛谷，原作者为

	WeLikeStudying 

搬运于2025-08-24 22:38:33，当前版本为作者最后更新于2022-05-28 08:53:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

• 以前作者的措辞可能不太恰当，但是我觉得这是能够理解的，毕竟作者早已退役，$\text{APIO}$ 比赛，就算规模再大，对我来说只有思维训练的价值而已。
• 如果各位不嫌弃我的祝福的话，我希望大家不要留下遗憾。

题意

• 输出一个排列，满足它存在恰好 $k$ 个递增子序列（包括空序列）。
• 你需要使得排列长度不大于 $90$，$k\le 10^{18}$。
• 多测，测试组数不超过 $100$。

分析

• 一个小的部分分：$k\le 90$。
• 输出长度为 $k-1$ 的逆序排列代码，信息复杂度 $O(k)$，最坏情况显然是需要用 $10^{18}-1$ 个数表示 $10^{18}$，理论得分 $10$，实际得分 $10$。
• 你采取任何一种合法构造方法都能拿到这 $10$ 分，因为这已经是可能构造出来的最长排列了。
• 是构造题呢，仔细思考一下，构造这样一种排列：所有合法的不下降子序列都不能跨过一个范围。
• （上图实际的形状：多段连续的上升子序列，其中相对前面的段的元素严格大于后面的段）
• 现在问题就变成了：给定 $n\le90$ 个数 $a_i$，满足：

• 然后就可以构造了，不论怎么样都不会超过 $90$ 个数吧（flag）（upd：flag 没了）。
• 代码，信息复杂度 $O(\log^2k)$，更具体地，它需要用 $1713$ 个数来表示 $2^{59}+2^{58}-58$，理论得分 $65.49$，实际得分 $71.2$。
• 我似乎建立了一个钢琴的模型，如下图：
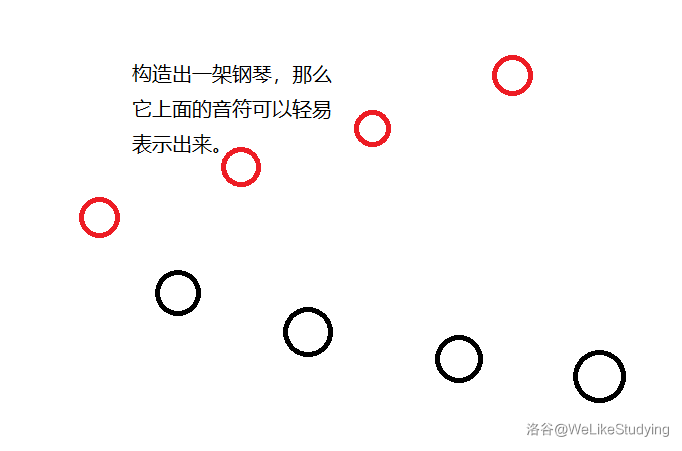
• （上图实际的形状：一个严格上升序列，一个严格下降序列，交错摆放，且上升序列的数严格大于下降序列）
• 考虑每个黑点右上方有多少个红点，那么黑点的贡献是关于二的指数，可以发现这个结构很适合拆位，代码，信息复杂度 $O(\log k)$，更具体地，它需要用 $117$ 个数来表示 $2^{59}+2^{58}-1$，理论得分 $91$，实际得分 $91.36$。
• 类题，接下来进入玄学领域：卡常，因为能用长度不超过 $n$ 的数列表示的数（不论它具体是啥）大小显然绝对不超过 $\lceil \log_2 k\rceil$（毕竟你至少要表示得出这么大的数才行）。
• 所以 $O(\log k)$ 是一个不可逾越的理论下限，在这个时候，常数就极其重要了，我们刚才的算法信息复杂度理论上是 $\lfloor\log_2k\rfloor+\operatorname{popcount}(k)-1$，即常数最坏为 $2$，但是这道玄学题目的常数最坏是 $1.5$。
• 奆佬的赛时想法，既然明确了正解不是它，那么它很可能得到满分（如果你有足够的代码实现功底的话）。
• 以下是和奆佬讨论的结果，奆佬的信息学直觉：$2^{60}$ 恰好在 $10^{18}$ 左右，而 $90=60\times 1.5$，实在是太整了，不像是乱搞的信息复杂度，正因为有了奆佬的提醒，才能有以下的思考，它的简洁和优美显示它确实是正解。
• 首先那个骨架是很难少的，所以我们就要针对 $\operatorname{popcount}$ 的常数下功夫。
• 如何做呢，容易发现这样一个性质：
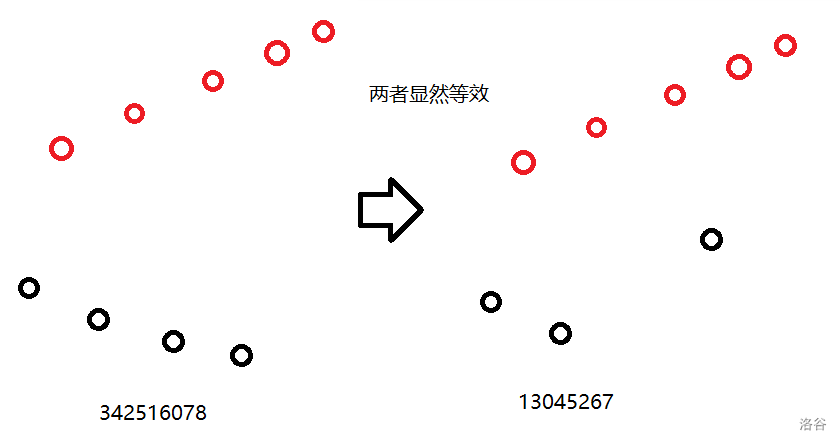
• 具体是为啥呢，原因就是如果其它的贡献单独考虑，而且把高上去的点与前两个点相互作用产生的权值累加的话，那么等价于这个高的黑点权值乘 $3$。
• 也就是说：如果我们在前面先定下了两个 $1$，那么后面就可以用一个 $1$ 来代表连续的两个 $1$。
• 看起来这种做法很有希望呢，那么采用这种做法最多要放几个黑颜色的点呢？假设 $k$ 足够大，我们最多放 $\lfloor0.5\log_2k\rfloor+1$ 个点，因为如果我们放两个 $1$，那么可以等价为 $11$ 占了两位，如果我们被迫放一个 $1$，那么可以等价为 $10$ 占了两位（或者到了结尾），总之：常数被卡到了 $1.5$，我们可以等着做出这题了。
• 这个做法的实现稍微麻烦一点，不过代码并不因此超过 $1\text{KB}$：代码，信息复杂度 $O(\log k)$，更具体地，它需要 $89$ 个数来表示 $2^{59}+2^{58}-1$，理论得分 $100$。