1 条题解
-
0
自动搬运
来自洛谷,原作者为

Swiftie_wyc22
AFO——2022.9.27搬运于
2025-08-24 22:38:31,当前版本为作者最后更新于2022-07-26 15:11:15,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
这道题其实很考思维的转换。
需要考虑如何将平面转换为线段,从而使用线段树?
线段树的基本操作就不讲了,可以去网上搜,再做做模板题。板子
思路是这样的:
枚举 轴,类似固定长度的滑动窗口,左点是 ,右点则是
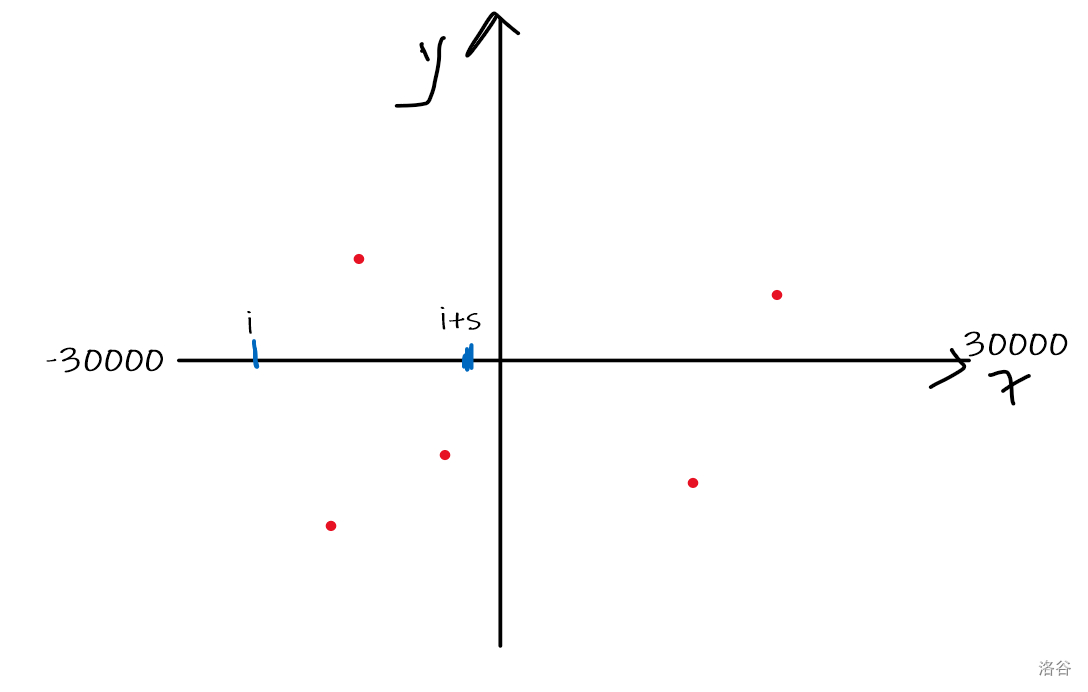
我们可以忽略高度,将这个图化为一维:
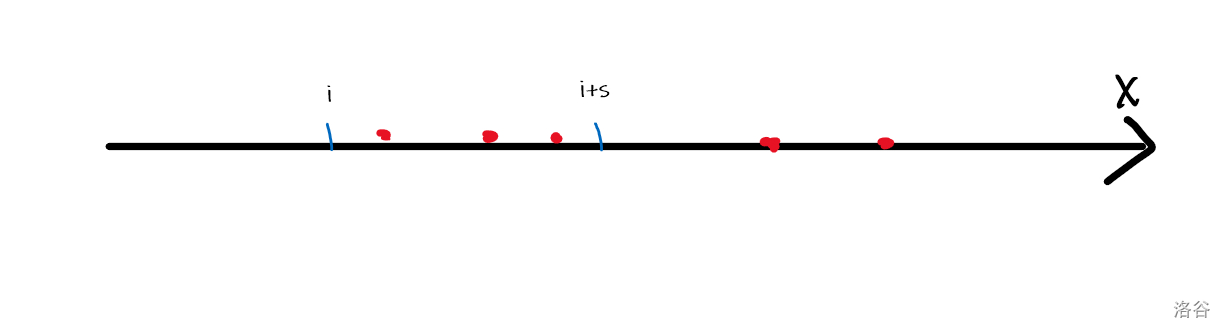
这个窗口( 下标)从 开始移动,移动到
我们只需要看的是窗口内的点数,则必然会有去除和加入的操作。去除和加入的操作也需要左右变量来实现。
这样枚举完,只需要算每一次 更新之后覆盖的最大值就可以!
那么问题来了,区间的覆盖最大值怎么算呢?那很显然,用线段树嘛。
这个树,则需要建在 轴上!
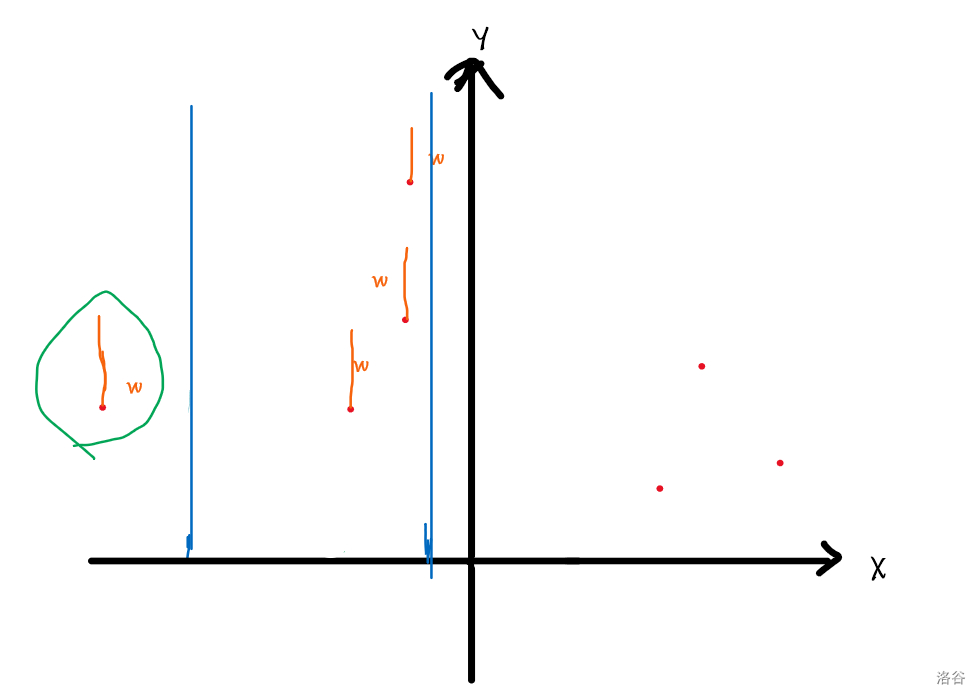
图中两条蓝色竖线即线段树的有效保留位置。在蓝色区间内的这些点,每个点的 到 都是有效覆盖范围,只需要将这些线段在线段树上 加一。然后我圈起来的那条线段,已经不在蓝色区间内,所以需要去除,则在线段树上把那条线段 减一!这种区间修改,需要懒操作。不会的要学学。
以上的操作称为一次更新吧,一次更新会出现一个最大值,我们只需要求每一次更新最后的最大值,就是最大覆盖数!因为有重叠的线段会重复覆盖,比如两条线段有一个覆盖部分,那么这两条线段的最大值都是 2。嗯大概就是这个意思(解释不清楚,逃)
这道题不需要离散化,如果数据量足够大,比如P1502,就需要离散化缩小空间。
代码就来了:
#include <iostream> #include <algorithm> using namespace std; #define MAXN 60000 #define LL long long const int Delta = 30001; struct Tree { int l, r; LL maxv; LL tag; }; Tree tree[4 * MAXN]; pair<int, int> a[15000]; int s, w, n; void build(int p, int l, int r) { tree[p].l = l; tree[p].r = r; tree[p].tag = 0; if (l == r) { tree[p].maxv = 0; return; } int mid = (l + r) / 2; build(2 * p, l, mid); build(2 * p + 1, mid + 1, r); tree[p].maxv = max(tree[2 * p].maxv, tree[2 * p + 1].maxv); } void pushdown(int p) { int l = 2 * p, r = 2 * p + 1; if (tree[p].tag != 0) { tree[l].tag += tree[p].tag; tree[l].maxv += tree[p].tag; tree[r].tag += tree[p].tag; tree[r].maxv += tree[p].tag; tree[p].tag = 0; } } void update(int p, int l, int r, LL v) { if (l <= tree[p].l && tree[p].r <= r) { tree[p].tag += v; tree[p].maxv += v; return; } pushdown(p); int mid = (tree[p].l + tree[p].r) / 2; if (l <= mid) update(2 * p, l, r, v); if (r >= mid + 1) update(2 * p + 1, l, r, v); tree[p].maxv = max(tree[2 * p].maxv, tree[2 * p + 1].maxv); } LL ask(int p, int l, int r) { if (l <= tree[p].l && tree[p].r <= r) return tree[p].maxv; pushdown(p); int mid = (tree[p].l + tree[p].r) / 2; LL ret = 0; if (l <= mid) ret = max(ret, ask(2 * p, l, r)); if (r >= mid + 1) ret = max(ret, ask(2 * p + 1, l, r)); return ret; } int main() { cin >> s >> w; cin >> n; for (int i = 0; i < n; i++) { cin >> a[i].first >> a[i].second; } build(1, -30000 + Delta, 30000 + Delta); sort(a, a + n, cmp); // sorting of pair array is accord '.first' from small to big int l = 0, r = -1; int ans = 0; for (int x = -30000; x <= 30000; x++) { int xx = x + s; while (l < n && a[l].first < x) { update(1, a[l].second + Delta, a[l].second + w + Delta, -1); l++; } while (r + 1 < n && a[r + 1].first <= xx) { update(1, a[r + 1].second + Delta, a[r + 1].second + w + Delta, 1); r++; } int tmp = tree[1].maxv; ans = max(ans, tmp); // cout << "ok" << x << " "; } printf("%d\n", ans); return 0; }
- 1
信息
- ID
- 7718
- 时间
- 1000ms
- 内存
- 128MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
