自动搬运

查看原文

来自洛谷，原作者为

	liangbowen 不能再摆了，，，

搬运于2025-08-24 22:38:16，当前版本为作者最后更新于2022-09-07 21:58:15，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

题目传送门！

更好的阅读体验？

困难的博弈论题目。参考了巨佬 @Kaenbyou_Rin 的题解，并对他题解中错误的地方进行了更改。

警告：以下内容稍长，请认真阅读，有一定数学基础就很容易理解，因为实际证明难度不高。这个是感性证明。

思路

首先给出结论：只要有一个节点的度是偶数，先手必胜；否则后手必胜（也就是：后手必胜当且仅当全部节点的度都是奇数）。

证明如下。为了方便叙述，设状态 $A$ 表示全部点度都是奇数。设每一步选择删除的点为 $u$。严谨说明，这里都是看 $n > 1$ 的情况。

首先很显然，状态 $A$ 的下一个状态一定不是 $A$。

因为 $u$ 连接的点都是两两不同的，所以删掉对应的边后，$u$ 所连接的点的度一定都会变成偶数。

这样不管选哪个连通块，必定有一个点度为偶数（也就是原本与 $u$ 相连的点）。

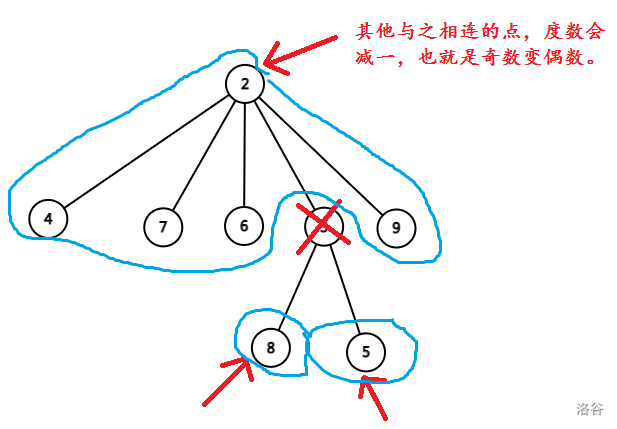
接着证明：不是 $A$ 的状态，必定可以转化为状态 $A$。

这个其实也不难，我们容易想到，必定有一个度为偶数的点，它有一棵子树，里面的所有点，度数都是奇数。

事实上，如果一个点不行，就换另一个点，依次枚举即可找到。

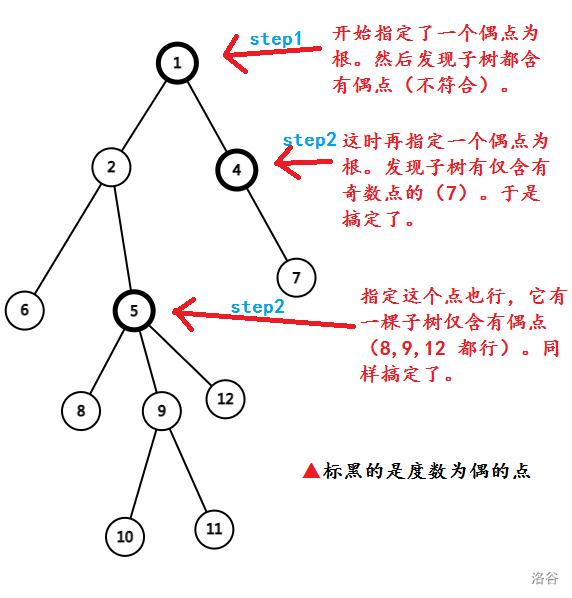
这一部分的具体证明：其实特别简单。

第一次指定根时我们有一棵树，然后如果没有满足要求的子树的话，我们直接从下往上找到深度最大的度为偶数的点。

这个点既然深度最深，那它下面必定都是度为奇数的点。这一部分就证掉了。

那我们知道这个有什么用呢？更简单了，直接通过删除其他点，保留下这个根以及全是奇点的子树。那么根的度就会变成 $1$。剩下的其他点又都是奇点，那不就变成状态 $A$ 了吗？

其实认真阅读上述内容，并不是很困难。如果不仔细证明的话，实际上几分钟就能想出以上两个结论。

有了这两个结论，接下来就很容易了吧。说白了就是：$A$ 必须变成非 $A$，非 $A$ 可以变成 $A$。

阅读题目，当对手将状态变为了 $n = 1$，你就赢了。$n = 1$ 代表着：非 $A$ 的状态。

也就是说，如果初始状态为非 $A$ 状态，先手将这个状态变为 $A$ 状态即可。对手很生气，因为他必须把这个状态再次变为非 $A$ 状态。

由于每次 $n$ 都会减少，而且先手每次都会获得一个非 $A$ 状态。所以迟早这个状态会是 $n = 1$，于是先手获胜了。

反过来，先手获得了 $A$ 状态，那么先手必须把这个状态变成非 $A$ 状态。这下后手变成了先手，同上操作即可。后手获胜。

其实很简单，对吧？

完整代码

十分简单精简。

#include <iostream>
#include <cstdio>
using namespace std;
int in[100005];
void solve()
{
	int n;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) in[i] = 0;
	for (int i = 1; i < n; i++)
	{
		int u, v;
		scanf("%d%d", &u, &v);
		in[u]++, in[v]++;
	}
	for (int i = 1; i <= n; i++)
		if (in[i] % 2 == 0) //度为偶数，先手必胜 
		{
			puts("Hifuu");
			return;
		}
	puts("Luna");
}
int main()
{
	int T;
	scanf("%d", &T);
	while (T--) solve();
	return 0;
}

希望能帮助到大家！