自动搬运

查看原文

来自洛谷，原作者为

	luogubot luogubot

搬运于2025-08-24 22:38:10，当前版本为作者最后更新于2022-05-17 20:30:46，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先知道 $S=\{x_1,x_2,\cdots x_k\}(x_i\leq x_{i+1})$ 能凑出的上界是 $\sum x_i$，然后断言能达到上界当且仅当「$\forall k\in[1,\sum x_i]$，$S$ 中 $\leq k$ 的数之和 $\ge k$」，证明略。令 $f_i$ 是若干个 $[1,i]$ 中的数之和是 $i$ 且满足上述条件的方案数，答案就是 $2^n-\sum f_i\times 2^{n-i-1}$，即在非法方案中钦定 $i+1$ 不选，剩余的任意选择，每个方案都能在第一次非法的时候被减掉。

考虑通过容斥求出 $f$，即设 $g_i$ 是若干个 $[1,i]$ 中的数之和是 $i$ 但不限制满足上述条件的方案数，它的求法将在之后讨论，然后 $f_i=g_i-\sum f_j\times val(j,i)$，其中 $val(j,i)$ 表示转移的系数。从 $j$ 转移到 $i$ 意味着从 $j+1$ 开始就不合法了，于是 $j+1$ 这个数是不能选的，只能选 $[j+2,i]$ 中的若干个数使其和为 $j-i$，$val(j,i)$ 就是这样的方案数。

我们暂时搁置 $f$ 的转移，来看 $g$ 的 $O(n\sqrt n)$ 经典 dp。$g_n$ 是若干不同正整数和为 $n$ 的方案数，因为 $\sum_{i=1}^n i=O(n^2)$，于是凑出 $n$ 的正整数只有 $O(\sqrt n)$ 个，我们把选择的数看作格子画出来：

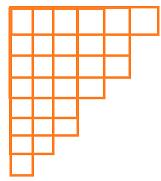
一列的格子数对应一个选择的数组，比如这就对应选择了数字 $\{8,7,6,4,3,1\}$。这样的好处是列数，即行的长度只有 $O(\sqrt n)$，每一行的长度单调不增且与上一行的差值不超过 1，如果超过 1 就出现了两个相同的数了；一行长度为 $i$ 的格子表示给最大的 $i$ 个数加一。

问题就转化为可以在行上做完全背包了，从 $O(\sqrt n)$ 到 1 枚举行的长度，并强制这个长度至少有一行，然后做完全背包就可以对应拆分的方案数了，复杂度 $O(n\sqrt n)$。代码长这样（Rof 是倒序循环）：

Rof(i,n,1)if(1ll*i*(i+1)/2<=n){
    Rof(j,n,i)g[j]=g[j-i];
    add(g[i],1);For(j,i,n)add(g[j],g[j-i]);
}

其中 add(g[i],1) 表示加入一种第一行长度是 $i$，即只选 $i$ 个数的方案。

然后再考虑 $f$ 的转移，$f_i=g_i-\sum f_j\times val(j,i)=g_i-h_i$。我们不会求出每个 $val(j,i)$ 精确的值，但我们知道 $val(j,i)$ 等于在 $[j+2,i]$ 中选若干个和为 $j-i$ 的方案数，那么 $h$ 转移和 $g$ 唯一的不同就在于加入一种第一行有 $i$ 个格子（选了 $i$ 个数）的方案时，首先有一个 $f_j$ 作为被加入的方案数替代原本的 1，然后需要选 $i$ 个 $\ge j+2$ 的数，和就变为了 $j+(j+2)i$，也就是 $f_j\to h_{j+(j+2)i}$，$j$ 在内层枚举。

注意到在转移 $h$ 前必须把转移过来的 $f$ 的 dp 值提前计算完成，可以每次先求出前一半的 dp 值，再转移给后一半，即由于 $j+(j+2)i\ge 2j$，可以倍增完成转移。

复杂度 $n\sqrt n+\frac{n\sqrt n}2+\frac{n\sqrt n}4+\cdots=O(n\sqrt n)$，阅读完整代码可能更有助于理解，注意代码中的变量意义和题解描述不完全相同。