自动搬运

查看原文

来自洛谷，原作者为

	dyc2022 「知らない世界を見せてよ」

搬运于2025-08-24 22:38:06，当前版本为作者最后更新于2025-07-21 18:51:13，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

更好的阅读体验

---

这题的难点在于把三角坐标系独立集转化为六边形的菱形覆盖。这里提供一种不同的转化方式。

接下来，以 $a = b = c = 2$ 为例。

---

如下图，我们可以画出 $a = b = c = 2$ 的情形。我们会发现，抠掉 $x,y$ 均为偶数的点，剩余部分应该是由若干个六边形拼接而成。

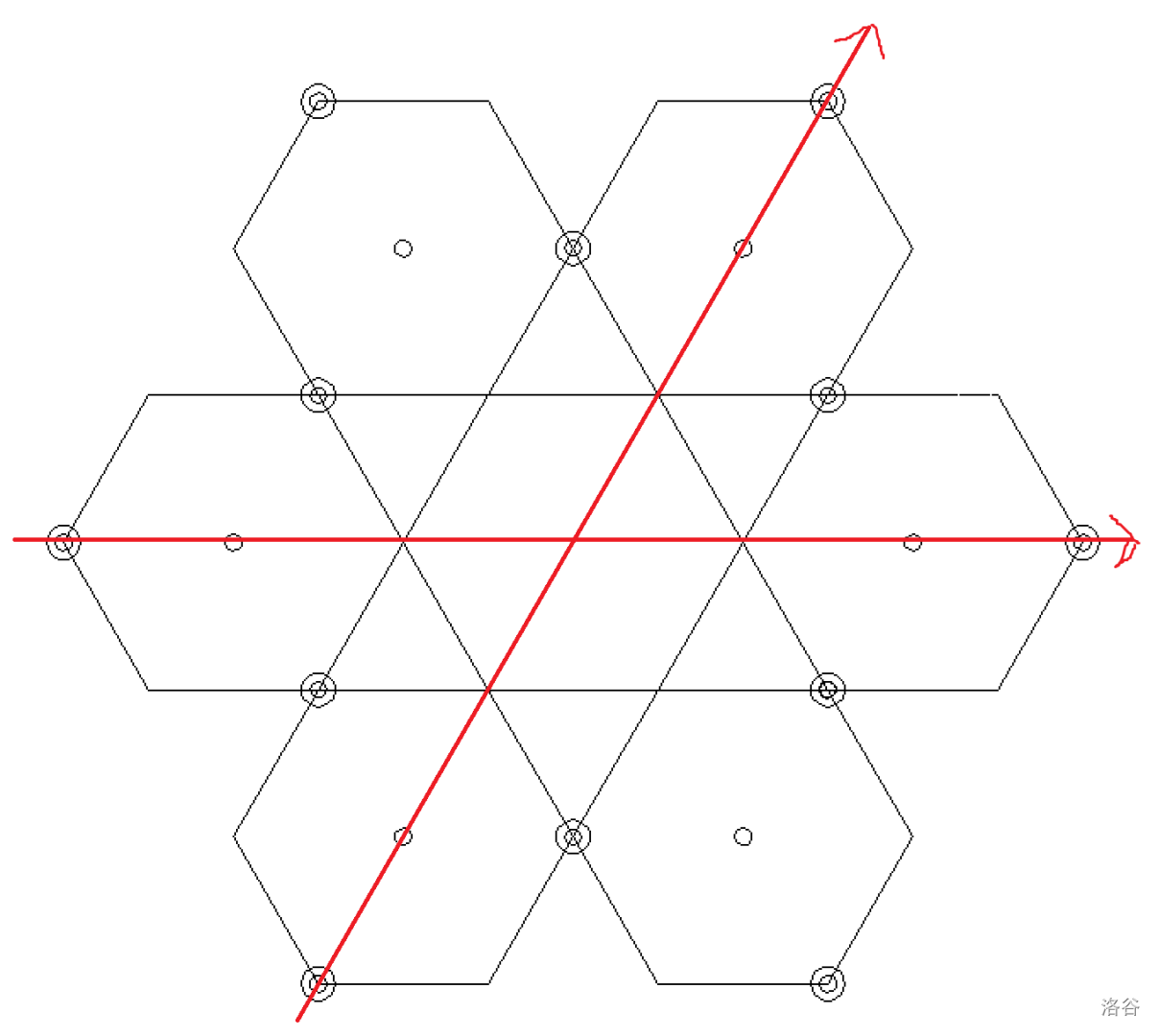
其中，红色为坐标系，线段的交点为可以选择的点，空心圆为六边形的中心。图中的黑色同心圆为我们选出来的一种最大独立集方案。

接下来，我们在图形的外围再套上一圈大六边形，使大六边形顶点到内圈顶点的距离等于小六边形边长，如下图。

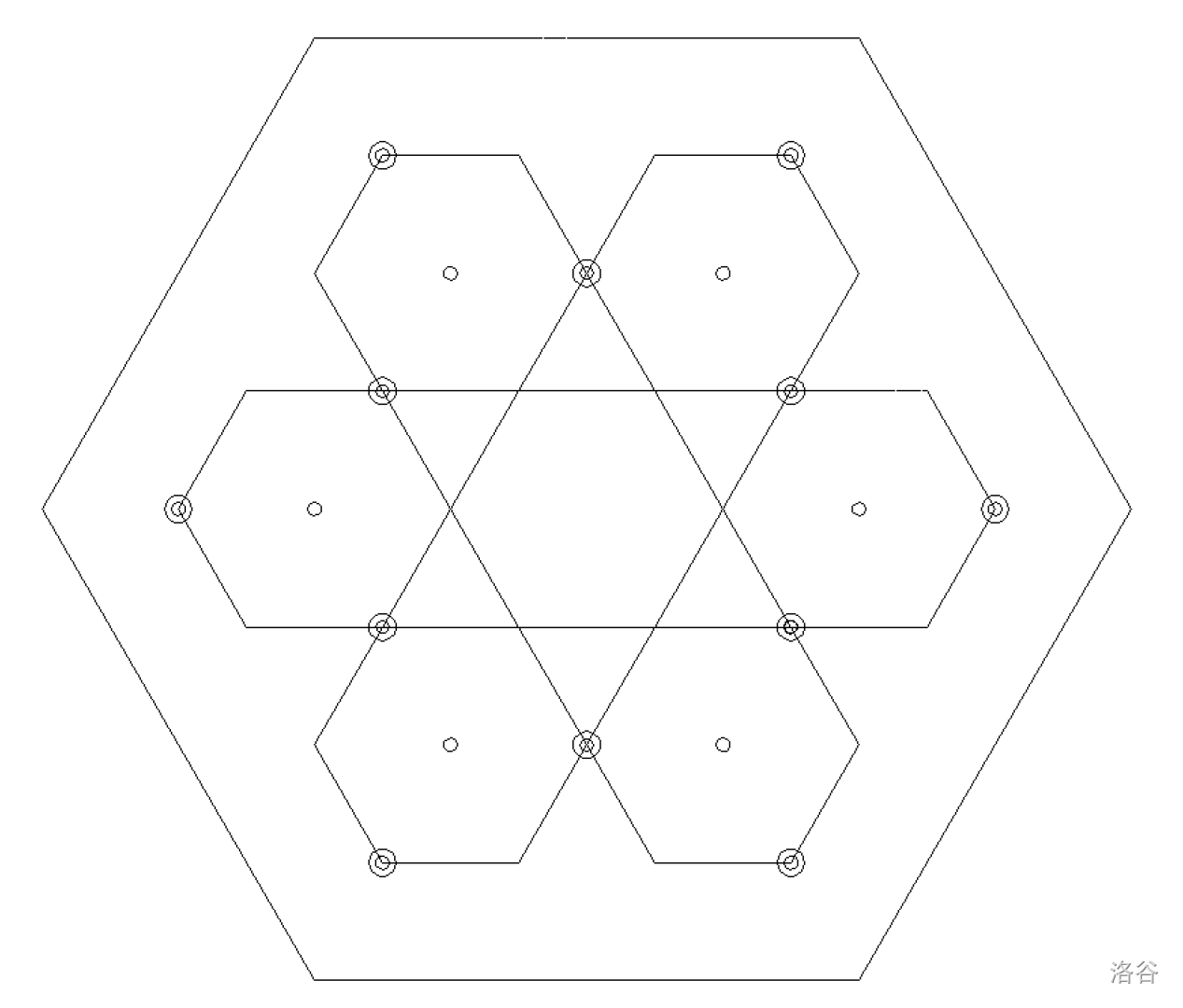
现在图中的点会分成两部分：选择的点和非选择的点，包括坐标为偶数的点和可以选择但是未被选择的点。

我们可以通过连接一些未选择的点，并延长至大六边形的边，将大六边形分割成若干部分。如图示情况下可构造如下。

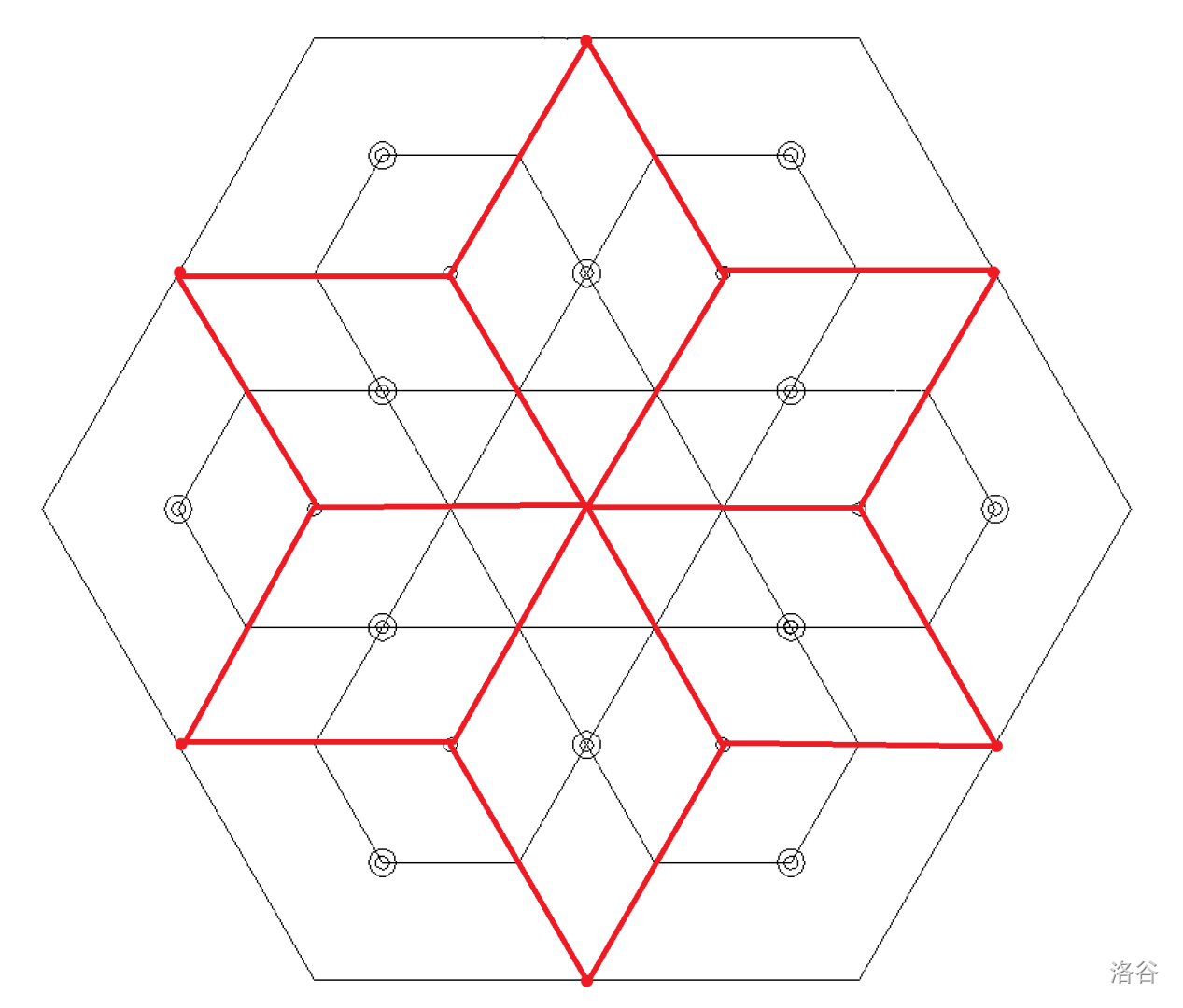
结果非常 amazing 啊！我们把大六边形分割成了若干个菱形，并且每个选择的点恰好就在每个菱形的中心。

假设大六边形边长为 $a',b',c'$，那么问题就转化成了给定一个边长确定的六边形，求其菱形分割方案数。

到这里还毫无头绪，我们不妨把这张图染个颜色。图中的菱形有三种朝向，我们对相同的朝向染相同的颜色，如图。

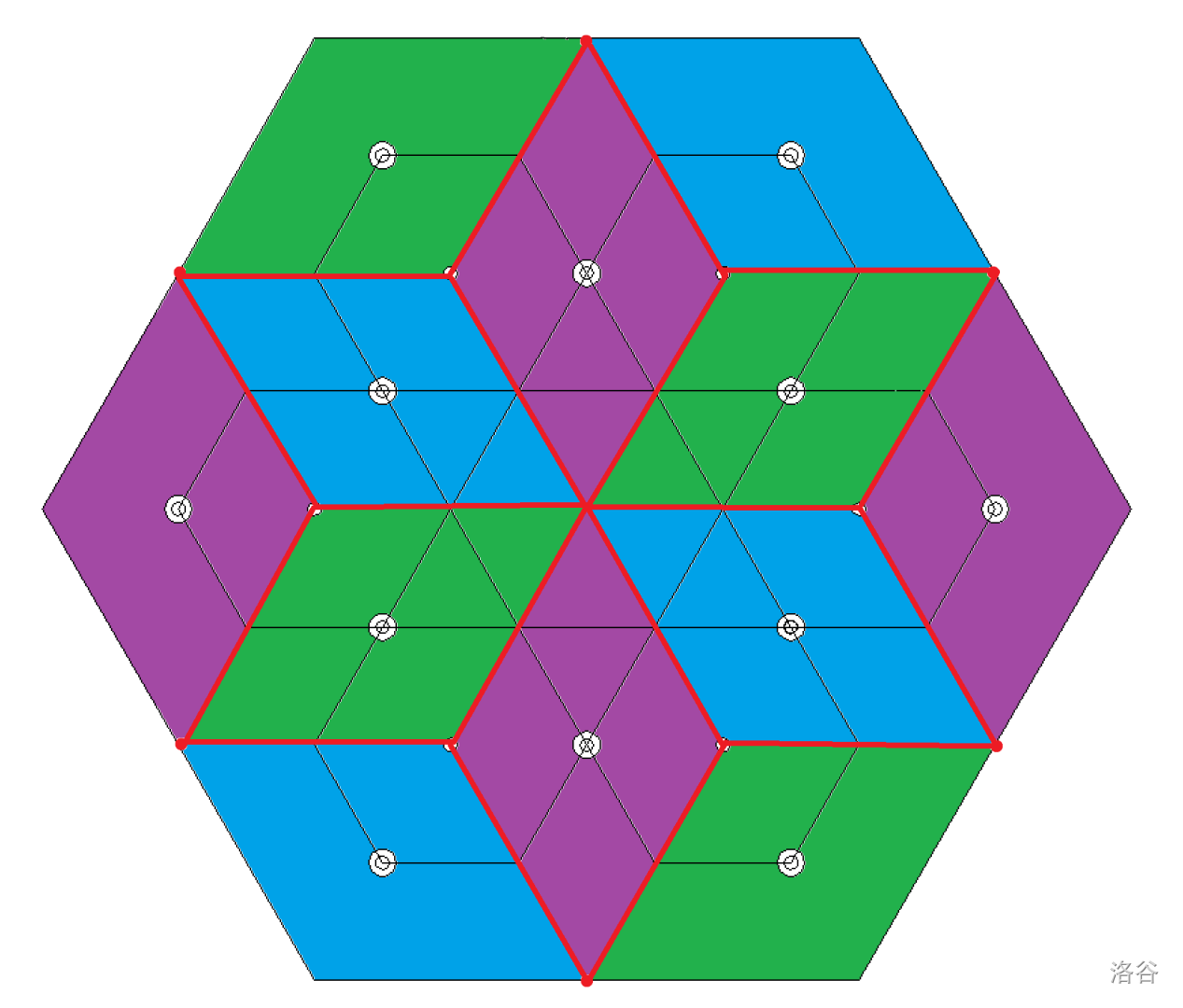
把脑袋（屏幕）旋转一个角度，然后盯着这个图看，你会发现这个东西看起来就像一堆正方体堆在墙角。

那么问题就变成了在空间直角坐标系堆正方体的方案数，并且通过观察，我们会发现必须要满足一个点前面和右边的堆叠个数要小于等于这个点的堆叠个数。给每行、每列加上一个倒序等差数列，发现变成了一个杨表。

---

那么剩下就是 dirty work 了。对于杨表 $\lambda$，根据钩子公式，答案就是

$$\prod _{(i,j)\isin \lambda}\frac{a'+c'-j-i}{\operatorname{hook}(i,j)}=\prod ^{a'}_{i=1}\prod^{b'}_{j=1}\frac{a'+c'-j-i}{a'+b'-i-j+1} $$

展开可得

$$\prod_{i=1}^{a'}\frac{(a'+b'+c'-i)!(a'-i)!}{(a'+c'-i)!(a'+b'-i)!} $$

构造 $f(i) = \prod\limits_{j=1}^{i}i!$，带回原式则有

$$\frac{f(a'-1)f(b'-1)f(c'-1)f(a'+b'+c'-1)}{f(a'+b'-1)f(b'+c'-1)f(a'+c'-1)} $$

那么这道题就做完了，预处理 $f(i)$ 和 $f^{-1}(i)$，复杂度显然线性。

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define N 3000006
#define MOD 998244353
using namespace std;
int fac[N],ifac[N],f[N],invf[N],T,a,b,c,x,y,z;
int qpow(int x,int y)
{
    if(y==0)return 1;if(y==1)return x%MOD;
    int ret=qpow(x,y>>1);return ret*ret%MOD*qpow(x,y&1)%MOD;
}
void init()
{
    fac[0]=f[0]=invf[0]=1;
    for(int i=1;i<N;i++)
        fac[i]=fac[i-1]*i%MOD,f[i]=f[i-1]*fac[i]%MOD;
    ifac[N-1]=qpow(fac[N-1],MOD-2);
    for(int i=N-2;~i;i--)
        ifac[i]=ifac[i+1]*(i+1)%MOD;
    for(int i=1;i<N;i++)
        invf[i]=invf[i-1]*ifac[i]%MOD;
}
main()
{
    scanf("%lld",&T),init();
    while(T--)
    {
        scanf("%lld%lld%lld",&x,&y,&z),x=min(x,y+z),y=min(y,x+z),z=min(z,x+y);
        a=x+y-z,b=x+z-y,c=y+z-x;
        printf("%lld ",a*b+b*c+c*a);
        if(!a||!b||!c){printf("1\n");continue;}
        int ans=f[a-1]*f[b-1]%MOD*f[c-1]%MOD*f[a+b+c-1]%MOD*invf[a+b-1]%MOD*invf[b+c-1]%MOD*invf[a+c-1]%MOD;
        printf("%lld\n",ans);
    }
    return 0;
}

---

感谢信友队孔启皓老师的讲解。

感谢 Microsoft Windows Logo 提供粗劣高超的绘图支持。