自动搬运

查看原文

来自洛谷，原作者为

	Thunder_S 咖啡馆与广场有三个街区，就像霓虹灯到月亮的距离。

搬运于2025-08-24 22:38:03，当前版本为作者最后更新于2022-07-02 15:59:23，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Solution

看到任意两点均不互连，想到与之类似的强连通分量，预示着这题将使用 $\text{Tarjan}$ 来完成。

先考虑把边的方向确定下来。

注意到有贡献的连法只有以下三种：

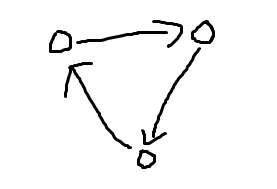
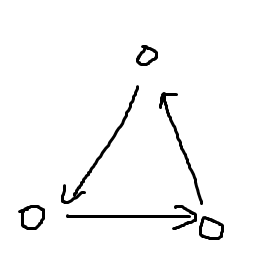
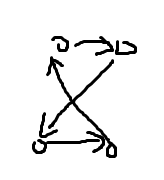
观察发现，这三种连法中右下的点一定是向左上连出的。

根据这个发现，我们有了以下思路：

1. 将边排序，第一关键字 x 从小到大（上河岸），第二关键字 y 从大到小（下河岸）。

2. 枚举每条边，如果当前边下河岸的点在目前所有边的最右端，那么说明这个点在某种连法中一定处在右下的位置，所以此边的类型为 1。

3. 其余边类型为 0。

现在已经确定了边的方向，剩下的就是模板题：有向图中求强连通分量的个数。

Code

#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 400005
using namespace std;
int na,nb,n,m,tot,num,mx,cnt,ans,sum[N],sta[N*10],dfn[N<<1],low[N<<1];
bool bj[N<<1];
struct node {int x,y,id;} edg[N];
struct edge {int to,next,head;} a[N*3];
bool cmp(node x,node y)
{
    if (x.x<y.x) return true;
    if (x.x>y.x) return false;
    return x.y>y.y;
}
void add(int x,int y) {a[++tot].to=y;a[tot].next=a[x].head;a[x].head=tot;}
void dfs(int x)
{
    dfn[x]=low[x]=++cnt;
    sta[++num]=x;
    bj[x]=true;
    for (int i=a[x].head;i;i=a[i].next)
    {
        int y=a[i].to;
        if (!dfn[y]) dfs(y),low[x]=min(low[x],low[y]);
        else if (bj[y]) low[x]=min(low[x],dfn[y]);
    }
    if (dfn[x]==low[x])
    {
        ++ans;
        while (sta[num]!=x) bj[sta[num--]]=false;
        bj[sta[num--]]=false;
    }
}
int main()
{
    freopen("neverland.in","r",stdin);
    freopen("neverland.out","w",stdout);
    scanf("%d%d",&na,&nb);
    for (int i=1;i<na;++i)
        add(i,i+1);
    for (int i=1;i<nb;++i)
        add(i+na,i+na+1);
    scanf("%d",&m);
    for (int i=1;i<=m;++i)
        scanf("%d%d",&edg[i].x,&edg[i].y),edg[i].id=i;
    sort(edg+1,edg+m+1,cmp);
    for (int i=1;i<=m;++i)
    {
        if (edg[i].y>mx) mx=edg[i].y,add(edg[i].y+na,edg[i].x),sum[edg[i].id]=1;
        else add(edg[i].x,edg[i].y+na),sum[edg[i].id]=0;
    }
    n=na+nb;
    for (int i=1;i<=n;++i)
        if (!dfn[i]) dfs(i);
    printf("%d\n",ans);
    for (int i=1;i<=m;++i)
        printf("%d ",sum[i]);
    return 0;
}