自动搬运

查看原文

来自洛谷，原作者为

	xyz105 The talkers are talking about how to talk with other talking talkers.

搬运于2025-08-24 22:37:55，当前版本为作者最后更新于2024-05-31 21:29:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目描述

有一座城市，它可以被看作由 $n$ 个社区组成的树形结构。现要求选出其中 $k$ 个社区建公园，目标是使得 每个社区到最近公园的距离的最大值最小。输出这个最小距离和具体建造方案。

前言

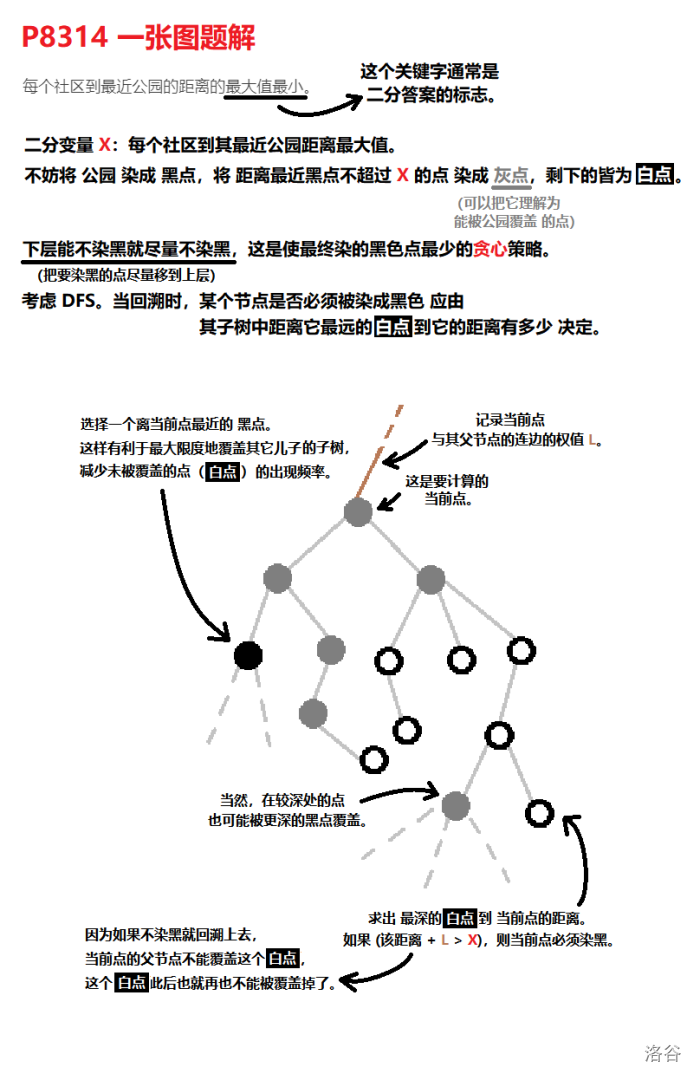
解题思路

二分答案。此处二分的值应为“每个社区到其最近公园距离最大值”（设其为 $x$），将原问题变为判定“在满足 $x$ 的限制下建造的公园数目能否 $\le k$”。

贪心。在满足 比公园深的节点 到公园的距离 $\le x$ 的限制下，将公园尽量往浅层建，对于那些 比公园浅的节点 固然是更优的，因为这样能使建造的公园总数更少。

DFS。在 DFS 过程中决定每个节点是否建造公园；当回溯到某个节点时，这个节点是否建造公园 应由 该节点 到 它子树中最远的未被其它公园覆盖的节点（下文称作“最远未覆盖节点”）有多远 作为依据。此处“节点被其它公园覆盖”指 节点到其它公园的距离已经 $\le x$ 了。

• 将“节点 $u$ 到‘最远未覆盖节点’的距离”记作 $d\_max_u$。如何求 $d\_max_u$？容易想出如下式子：$d\_max_u=\max \limits_{v\isin son_u} \{d\_max_v+w_{u,v}\}$。特别地，点 $u$ 的“最远未覆盖节点”不存在 当且仅当 $d\_max_u=-\infty$。

• 小问题是，对于点 $v\isin son_u$，点 $v$ 的“最远未覆盖节点”有可能被 $son_u$ 中除 $v$ 以外的其它节点的子树中的公园所覆盖。为了解决这个问题，将“节点 $u$ 到 其子树中最近公园 的距离”记作 $d\_min_u$，则上述式子变为：

$$d\_max_u=\max \limits_{v\isin son_u,\ d\_min_u+d\_max_v+w_{u,v}>x} \{d\_max_v+w_{u,v}\} $$

此为本题关键。下面讲一下代码实现细节：

• 初值：$d\_min_u=\infty,d\_max_u=-\infty$。先求出 $d\_min_u$。若点 $u$ 本身也是未被覆盖的节点（即 $d\_min_u>x$），则用 $0$ 去更新 $d\_max_u$。

• 特别地，如果 $u$ 为根节点 且 它的“最远未覆盖节点”存在（即 $d\_max_u\neq -\infty$），那么点 $u$ 无论如何都要建造公园。

• 输出答案时，如果该方案下建造的公园数 $<k$，则随机乱建新的公园直到公园数 $=k$ 为止。

说到底就是我那张“一张图题解”的补充说明而已。

参考代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

typedef long long ll;

const int MAXN = 2e5 + 10;

const ll INF = 0x3f3f3f3f3f3f3f3fll;

int n, k;

int head[MAXN], to[MAXN << 1], nxt[MAXN << 1], cnt;
ll w[MAXN << 1];

inline void add_edge(int u, int v, ll w2)
	{to[++cnt] = v, w[cnt] = w2, nxt[cnt] = head[u], head[u] = cnt;}

int fcnt = 0;
bool chosen[MAXN], res[MAXN];
int ans1[MAXN];
ll dis_mx[MAXN], dis_mn[MAXN];

void dfs(int u, int fa, ll w2, ll x)
{
	dis_mn[u] = INF, dis_mx[u] = -INF;
	for (int i = head[u]; i; i = nxt[i])
		if (to[i] != fa)
			dfs(to[i], u, w[i], x),
			dis_mn[u] = min(dis_mn[u], dis_mn[to[i]] + w[i]);
	
	if (dis_mn[u] > x) dis_mx[u] = max(dis_mx[u], 0ll);
	for (int i = head[u]; i; i = nxt[i])
		if (to[i] != fa && dis_mn[u] + dis_mx[to[i]] + w[i] > x)
			dis_mx[u] = max(dis_mx[u], dis_mx[to[i]] + w[i]);
	
	if (dis_mx[u] + w2 > x || (u == 1 && dis_mx[u] != -INF))
		fcnt++, chosen[u] = 1, dis_mn[u] = 0, dis_mx[u] = -INF;
}

bool judge(ll x)
{
	memset(chosen, 0, sizeof(bool) * (n + 5));
	fcnt = 0, dfs(1, 0, 0, x);
	return fcnt <= k;
}

int main()
{
	scanf("%d%d", &n, &k);
	for (ll i = 1, i1, i2, i3; i < n; i++)
		scanf("%lld%lld%lld", &i1, &i2, &i3),
		add_edge(i1, i2, i3), add_edge(i2, i1, i3);
	
	ll l = 0, r = 1e15, mid, ans;
	while (l <= r)
	{
		mid = (l + r) >> 1;
		if (judge(mid)) memcpy(res, chosen, sizeof(bool) * (n + 5)), ans = mid, r = mid - 1;
		else l = mid + 1;
	}
	
	int i1 = 0;
	for (int i = 1; i <= n; i++) if (res[i]) ans1[++i1] = i;
	for (int i = 1; i <= n && i1 < k; i++) if (!res[i]) ans1[++i1] = i;
	
	printf("%lld\n", ans);
	for (int i = 1; i <= k; i++) printf("%d ", ans1[i]);
	
	return 0;
}