自动搬运

查看原文

来自洛谷，原作者为

	鏡音リン 希望大家都能成为自己想要的样子呐

搬运于2025-08-24 22:37:38，当前版本为作者最后更新于2022-04-16 20:07:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

输出任意解是骗人的。我们直接把这题当最优化题，求出最优解，也就是转向角度最小的解。它是唯一的。

为了方便处理，出口位于终点左侧的部分一并算作左边界，右边界同理。

定义：对于合法范围内一点 $O$，如果存在点 $P,Q$ 使得：

• $O,P,Q$ 三点共线，且 $P$ 位于中间。
• $Q$ 的 $y$ 坐标大于 $O$。
• $P,Q$ 分别位于两侧的边界上。
• 线段 $OQ$ 完全位于合法范围内。

那么称 $P$ 为 $O$ 的尖点。

对于任意 $O$，我们可以用这样的方式找到 $O$ 的尖点。考虑从 $O$ 发射一道激光，从正左方向扫到正右方向。这个过程中，最开始激光照在左侧的墙上，一定有一个分割点，过了这个点激光就照在右侧的墙上。那么这个分割点激光相当于同时照在了两侧的墙上，两侧的墙各有一半的光点。这两个光点所在的位置就是 $P$ 和 $Q$，近的那个是 $P$，它就是尖点。如下图所示：

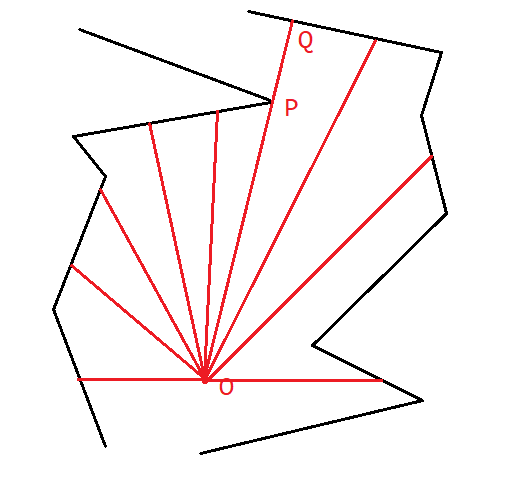
在一些极端情况下，在这个分割点的位置激光可能正好贴着一侧的墙壁，这时这一段墙壁上的所有点都可以是 $P$。我们可以人为地规定最远的那个 $P$ 是真正的 $P$。这样，尖点有且只有一个。而且过了 $P$ 之后，$P$ 所在的墙壁一定会向外拐，所以 $P$ 一定是”尖“的，所以它一定是边界的顶点或者终点。

下面放上最重要的结论：从 $O$ 开始到终点的最优路径必然经过 $O$ 的尖点。

考虑从 $O$ 开始到终点的路径一定穿过了线段 $PQ$，记穿过的点叫做 $R$。反证法，如果一条路径不过 $P$，那么 $O$ 到 $R$ 这一段一定不是线段 $OR$。考虑直接把这一段改成过 $P$ 的线段 $OR$，经过一些简单证明发现答案一定变优了（根据某定理，一定有一个时刻方向和线段 $PQ$ 相同，所以直接走这条线段是转向角度最小的）。因此不过 $P$ 的一定不是最优的。具体如下图所示，我们要把蓝线改成线段 $OR$。

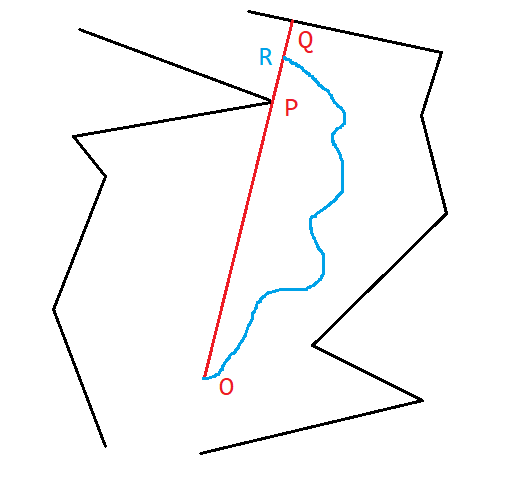
所以我们的算法就是，从起点开始，不断找到当前点的尖点，然后跳到那里，直到跳到终点（这时 $P,Q$ 和终点三点重合），找到的一定是最优路径。问题转化成了如何找到尖点。上述证明中，发射激光的那个方法其实就是找尖点的一种方式，不过不太好实现。

可以从前往后扫过去，并且模拟在 $O$ 点的视野，维护左墙在视野中最靠右的点和右墙视野中最靠左的点，一旦这两个点中间的缝隙消失就说明你找到了尖点。单次复杂度 $O(n)$，总复杂度最坏 $O(n^2)$。

但是数据是随的，这玩意 AC 了。期望复杂度多少我也不知道，反正能过。

正经做法：我们刚才维护的是两个点，把它们改成两个单调栈，维护两侧的凸包，也就是说，单调栈里每个元素都是它下面那个点视角最靠边的点，而栈底是当前点视角最靠边的点。其实就是凸包。

由于找到尖点之后，是把栈底那个点弹出来跳到那里（所以这实际上是个双端队列），栈里剩下的点还能接着用。这样每个点只会被扫一次，总复杂度 $O(n)$。