自动搬运

查看原文

来自洛谷，原作者为

	peppaking8 一起加油吧

搬运于2025-08-24 22:37:35，当前版本为作者最后更新于2022-04-04 10:12:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

USACO 的题都超有意思的。忘了题意的同志们，我们再来回顾一下：

题意

给定 $n$ 个点，$m$ 条边的无重边、自环的有向图。甲乙两人玩游戏，起初在图上 $x,y$ 点处各放一个棋子，甲先选择一个棋子，乙必须将这个棋子沿着边移动，还需保证两个棋子不重合。轮流进行这一过程，若乙不能移动则乙输，若游戏能无限进行则甲输。对 $q$ 组询问 $(x,y)$，求谁有必胜策略。$n,q\le 10^5$，$m\le 2\times 10^5$。

分析

在做完 P 组的 T3 后，发现第一题是 Benq 出的，所以很不可做，所以我们有大把的时间来好好研究这道 T2。所以我们一步步地分析这个题目。下面称题目中的脑 (Brain,B) 为甲，蹄 (Hoof,H) 为乙。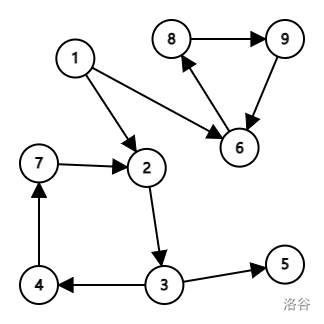

首先，观察样例的询问，为什么 $(1,5)$ 甲会赢呢？因为 $5$ 点没有出边，于是甲选择这个棋子，乙无处可走。所以初步想法是，如果有一个棋子所在的点出发只能走有限步，就一定是甲赢。如何找到这样的点呢？经典的处理办法是建反图跑拓扑排序，在拓扑序里的点就是无法到达环的点，自然只能走有限步。所以在接下来的分析中，可以将这些点删去，从而不妨设所有点出发都能到达环。

题目没有结束，我们注意到样例中还有 $(2,4)$ 甲会赢。甲可以指定 $4$，此时乙只能移动到 $7$，然后甲选 $7$，乙无处可走。也就是说，如果对于一个棋子所在点 $u$，它想走无限多步必须经过点 $v$，且另外一个棋子在 $v$，那么就是甲赢。这个要求感觉有些苛刻...有没有更一般的结论呢？

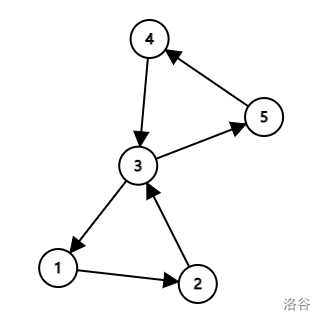
比如上图例子，如果棋子初始在 $(2,4)$，那么甲可以先选 $2$ 再选 $4$，这两个棋子都必须到 $3$，产生相遇，甲赢。所以说，我们还可以把这个结论加强，若 $u_1,u_2$ 想走无限步都一定会经过一个点 $v$，那么 $(u_1,u_2)$ 一定是甲赢。形式化地：

定义 $v$ 是 $u$ 的“支配点”，当且仅当 $u$ 走无限多步必须经过 $v$。也即，在删去 $v$ 后，$u$ 不在任何大小 $>1$ 的强连通分量内。$u$ 也是 $u$ 的支配点。令 $F(u)$ 为 $u$ 的所有支配点构成的集合，称为支配集。对于询问 $u_1,u_2$，若 $F(u_1)\cap F(u_2)$ 非空，则甲赢。

对于相交为空的情形，事实上乙会获胜，因为每次都可以避免走到另一个棋子的支配点上。所以至此我们已经找到了甲获胜的等价条件：支配集相交非空。

接下来自然就有了 $O(n^2+qn)$ 的算法：每次删掉一个点，看有多少点无法走到环上，就更新这些点的支配集。询问的时候直接暴力判交即可。事实上，后者还可以用 bitset 优化到 $O(\dfrac{qn}{w})$，可以通过测试点 1-9。

想要获得更加优秀的做法，就不能暴力求出支配集，而是研究支配的特殊性质。这里我们给出两条：

1. 传递性：$v$ 支配 $u$，$w$ 支配 $v$，则 $w$ 支配 $u$。
2. 偏序性：$v_1,v_2$ 都支配 $u$，则 $v_1,v_2$ 之间也有支配关系。

根据支配点的定义，容易证明以上两条。其中第二条给了我们启发：既然 $v_1,v_2$ 有共同支配的点，那么它们之间也会互相支配，也就是说，$u,v_1,v_2$ 两两有共同支配点。那么...如果将支配关系看作无向图的话，是不是连通块内的任两点都有共同支配点呢？

回顾 NOI2021 庆典。发现那道题对图的限制和第二条很相似，最后的结论是在缩强连通分量之后图为一棵树。强连通分量内的任两点自然有共同支配点；在树上的两点，因为它们共同指向祖先，那么它们也会有共同支配点——祖先！所以至此我们发现，若将支配的关系看作无向，那么连通分支里的任两点的支配集相交非空。

为什么这一结论十分重要？因为它让这道题变得可做：只需要找到不超过 $n-1$ 个支配关系，就能找到所有的连通分支，进而可以用并查集快速地处理询问！

那么如何找到这些支配关系呢？容易想到的是，若出度 $\deg u=1$，设 $u$ 连向 $v$，则 $v$ 一定支配 $u$。那再想，既然 $u,v$ 在支配关系图中同属一个连通块，那是否能在原图里把它们合并呢？事实上可以，因为但凡经过 $u$ 的点一定会下一步经过 $v$，故将他们合并起来并无大碍。合并时，注意 $u,v$ 缩成的点 $u'$ 可能存在自环。删去重边后，可能会出现新的 $u_0$ 满足 $\deg u_0=1$，就接着缩点就好了。为了快速地维护缩点的过程，我们可以回顾 WC2021 括号路径 这一题，用线段树合并/启发式合并解决。实现的好可以 $O(n\log n)$，不过两个 $\log$ 也问题不大。

当然在缩点后，虽然所有点的出度都 $\ge 2$ 了，但仍然不知道是否找全了支配关系。这时惊奇地发现：当前求出的连通分支就是正确的！

引理：若图中每个点的出度 $\ge 2$，则不存在任何不相同两点的支配关系。
证明：每次从 $u$ 都可找到不经过点 $v$ 的路径，故对任意 $u\not=v$，$v$ 都不支配 $u$。证毕。

至此我们解决了这道题。或许你在担心实现起来是不是非常麻烦，或是在后悔赛时没有想到正解...不过没关系，USACO 算什么 无论何时，只要领悟了这道题的精髓，从每道题里学到新知识，为什么不值得高兴呢？:)

Talk is cheap, show you the code... 提前声明，代码太丑，仅供参考~

#include<bits/stdc++.h>
using namespace std;
const int N=100005;
int n,m,q;
struct Edge{
	int u,v;
	int nxt;
}edge[N<<1];
int head[N],tot=0;
int ind[N],outd[N];
bool ok[N];
int fa[2][N];
int rt[2][N];
struct Tree{
	int siz;
	int ch[2];
}t[N<<6];
int ttot=0,was[N<<5],wastot=0;
bool have[N];
queue<int> tq;
string ans;
inline void add_edge(int u,int v){
	tot++;
	edge[tot]=(Edge){u,v,head[u]};
	head[u]=tot;
	ind[v]++,outd[u]++;
}
#define lson t[id].ch[0]
#define rson t[id].ch[1]
inline void pushup(int id){
	t[id].siz=t[lson].siz+t[rson].siz;
}
inline int NewNode(){ // 加了空间回收，不然会 MLE
	if(wastot){
		return was[wastot--];
	}
	return (++ttot);
}
inline void addwas(int id){
	if(wastot>=(N<<5)) return ;
	t[id].siz=t[id].ch[0]=t[id].ch[1]=0;
	was[++wastot]=id;
}
void Add(int &id,int L,int R,int k,bool del){
	if(!id) id=NewNode();
	if(L==R){
		t[id].siz=del;
		if(!del) addwas(id),id=0;
		return ;
	}
	int mid=(L+R)>>1;
	if(k<=mid) Add(lson,L,mid,k,del);
	else Add(rson,mid+1,R,k,del);
	pushup(id);
	if(!t[id].siz) addwas(id),id=0;
}
bool Have(int id,int L,int R,int k){
	if(!id) return false;
	if(L==R&&t[id].siz) return true;
	int mid=(L+R)>>1;
	return (k<=mid)?Have(lson,L,mid,k):Have(rson,mid+1,R,k);
}
int Findson(int id,int L,int R){
	if(L==R) return L;
	int mid=(L+R)>>1;
	if(t[lson].siz) return Findson(lson,L,mid);
	else return Findson(rson,mid+1,R);
}
inline int find(int k,int x){
	if(x==fa[k][x]) return x;
	return fa[k][x]=find(k,fa[k][x]);
}
int shanx,shany;
void Merge(int &x,int y,int L,int R){
	if(!y) return ;
	if(!x) x=y;
	if(L==R){
		if(t[y].siz){
			Add(rt[1][shanx],1,n,L,1);
			int pp=find(0,L);
			Add(rt[0][pp],1,n,shany,0),Add(rt[0][pp],1,n,shanx,1);
			if(t[rt[0][pp]].siz==1 && !have[pp]) tq.push(pp);
		}
		t[x].siz=(t[x].siz|t[y].siz);
		return ;
	}
	int mid=(L+R)>>1;
	Merge(t[x].ch[0],t[y].ch[0],L,mid);
	Merge(t[x].ch[1],t[y].ch[1],mid+1,R);
	pushup(x);
}
inline int makemerge(int k,int x,int y){ // y merge in x
	int fx=find(k,x),fy=find(k,y);
	if(fx!=fy) fa[k][fy]=fx;
}
void Topo(){
	for(int i=1;i<=n;i++){
		if(!ind[i]) tq.push(i),ok[i]=true;
	}
	while(!tq.empty()){
		int tp=tq.front();tq.pop();
		for(int i=head[tp];i;i=edge[i].nxt){
			int v=edge[i].v;
			if(!(--ind[v])) tq.push(v),ok[v]=true;
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		add_edge(v,u);
	}
	Topo();
	for(int i=1;i<=m;i++){
		int u=edge[i].u,v=edge[i].v;
		if(ok[u] || ok[v]) continue;
		Add(rt[0][v],1,n,u,1);
		Add(rt[1][u],1,n,v,1);
	}
	for(int i=1;i<=n;i++){
		fa[0][i]=fa[1][i]=i;
		if(ok[i]) continue;
		if(t[rt[0][i]].siz==1) tq.push(i);
	}
	while(!tq.empty()){
		int tp=tq.front();tq.pop();
		int now=find(0,tp),now1=find(1,tp);
		if(t[rt[0][now]].siz!=1 || have[now]) continue;
		int to=Findson(rt[0][now],1,n),nowto=find(0,to),nowto1=find(1,to);
		makemerge(0,to,tp);
		if(Have(rt[0][nowto],1,n,now1)) Add(rt[0][nowto],1,n,now1,0),Add(rt[1][now1],1,n,nowto,0),have[nowto]=true;
		Add(rt[1][nowto1],1,n,now,0);
		if(t[rt[1][now1]].siz < t[rt[1][nowto1]].siz){
			makemerge(1,nowto1,now1);
			shanx=nowto1,shany=now1,Merge(rt[1][nowto1],rt[1][now1],1,n);
		}
		else{
			makemerge(1,now1,nowto1);
			shanx=now1,shany=nowto1,Merge(rt[1][now1],rt[1][nowto1],1,n);
		}
	}
	scanf("%d",&q);
	for(int i=1;i<=q;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		if(ok[u] || ok[v]){
			ans+='B';
			continue; 
		}
		int fu=find(0,u),fv=find(0,v);
		if(fu==fv) ans+='B';
		else ans+='H';
	}
	cout<<ans<<endl;
}