自动搬运

查看原文

来自洛谷，原作者为

	jgvccc Always break, never continue.

搬运于2025-08-24 22:37:17，当前版本为作者最后更新于2022-04-02 23:23:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目传送门

显然，这道题不能用暴力做，因为仅仅计算单个的问题，就会达到 $10^9$ 的复杂度。

这个时候就需要考虑其他方法了。

因为这道题求的是余数的和，所以 最理想 的情况答案应为 $(a-1)+(b-1)$ （如下图所示）。但是这种情况的出现当且仅当 $(a,b]$ 区间内存在 $a,b$ 的公倍数的时候。

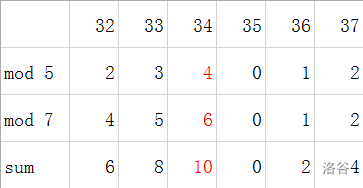
我们可以新建一个变量 $t$ 存储 $a$ 与 $b$ 的最小公倍数，然后对于每个询问，存储 $l \div t$ 和 $r \div t$ 的值。如果这两个值不相等，则可判断为上文中提及的情况，条件如下。

if(l \ t != r \ t)

不过，当 $l \div t = r \div t$ 时，这种方法就不奏效了，因为区间几乎不可能出现我们所期望的值了（如下图）。

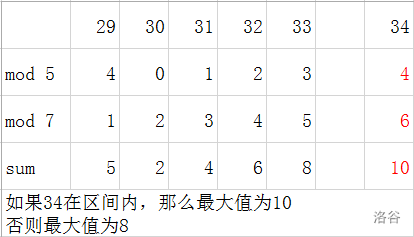
因为本蒟蒻不会倍增算法，所以 我们可以另辟蹊径。通过观察可以发现，在单独对一个数取余的两个序列中，会出现余数为 $0$ 的情况。而 $0$ 前面的数字则是这一行可能出现的最大数字。反过来推，可以得到： 如果一个数字的右边是0，那么它一定是该行最大的。如果不是0，那么它一定不是该行最大的。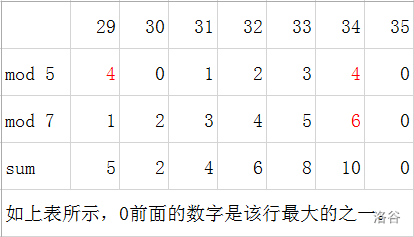

所以如果有一列的数右边都不是 $0$ ，那么可以直接排除这一列。所以我们 只需要扫一遍所有0左边的结果即可 ，这就大大减少了计算量，省去了很多时间复杂度。这还没完，千万不要忘记最右边的数也有可能是最大值，所以 最后一个数r也要扫 。

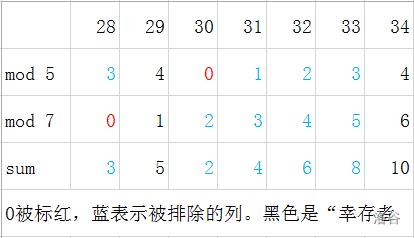
总结一下： 如果区间内存在最理想情况，直接输出。如果不存在，扫描一遍所有的 $0$ 左边的结果和 $r$ 。

上代码：

#include<bits/stdc++.h>
using namespace std;

int a,b,q,l,r,t,minn,maxn,ans;
int gcd(int a,int b)//最大公约数
{
    if(a % b == 0) return b;
    else return gcd(b,a % b);
}

int calc(int x)//计算结果
{
    return x % a + x % b;
}

signed main()
{
    std::ios::sync_with_stdio(false);
    cin>>a>>b;
    t = gcd(a,b);
    t = a * b / t;
    cin>>q;
    for(int i=0;i<q;i++)
    {
        cin>>l>>r;
        minn = l / t;
        maxn = r / t;
        ans = 0;
        if(minn != maxn) cout<<calc(maxn*t-1)<<endl;//最理想情况
        else
        {
            ans = calc(r);//千万别忘了扫这个位置
            for(int i = r/a*a-1;i>=l;i-=a) ans = max(ans,calc(i));//扫一遍除以第一个数余0的位置的左边并取最大值
            for(int i = r/b*b-1;i>=l;i-=b) ans = max(ans,calc(i));//扫一遍除以第二个数余0的位置的左边并取最大值
            cout<<ans<<endl;
        }
    }
    return 0;
}