自动搬运

查看原文

来自洛谷，原作者为

	€€£ 中国收钱协会(€hina€ounting£oundation)唯一官方认证账号，有事欢迎@（有时候可能不在）||https://www.luogu.com.cn/paste/hm8t61yq

搬运于2025-08-24 22:37:03，当前版本为作者最后更新于2022-03-22 14:36:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解（shadow）

我们先看看题目什么意思：最大的可能的阴影面积占总面积的比值 既然是比值，那么发现我们对于 有限面积 可以直接忽略；而对于两条固定的平行线的中间部分，由于圆的面积是随半径平方增长的，这部分面积是线性增长的所以最终不取这部分并不会对答案产生影响。（感谢 @_Solowing_ClCN 指出）

于是转化成了可能的最大角度；

发现答案不是 $3,4$​ 就是 $5$，接下来我们边讲做法边证明；

容易发现，三角形答案是 $3$，四边形答案是 $4$；

考虑我们求出凸包，发现如果里面还有点，那么 $3$ 次一定可行；

如果凸包上有一条边，它所在的两个端点都 mksha 一遍，如果 不能达到只用这两个能占1/2平面，那么一定要 $4$​ 次；因为除了这（些）边不能满，其余绝对是满的，而一个角最多是 $\pi$​​ ；

如果有一条边是这样，那么我们选如下图的四个角即可：

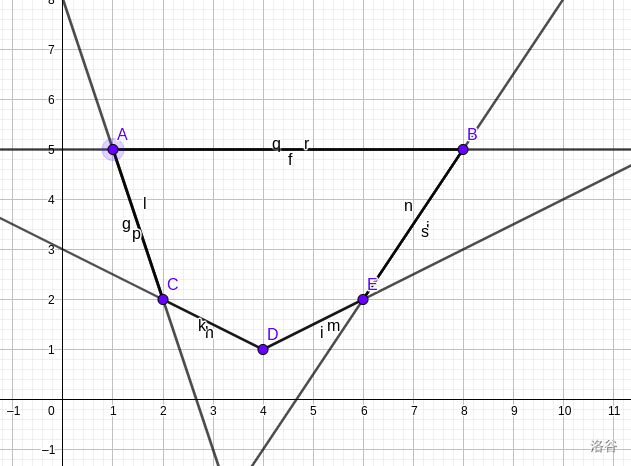
考虑到 $AC,EB$​ 都不是这样的边，所以一定可行；

如果有两条边是这样，那么我们选如下四个点即可：

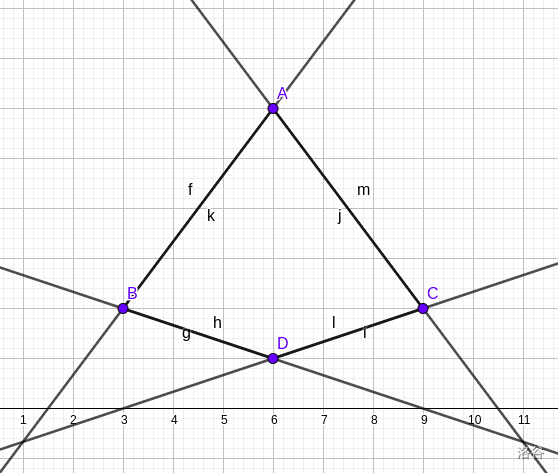
考虑到 $BD,DC$ 都不是这样的边，所以一定可行；

否则，我们可以用改编的旋转卡壳决定是否合法：我们选一个角，然后卡一个和它刚好角度范围有交的角，再卡一个和这个角有交的交，如果所有可能的三个角能够覆盖几乎整个平面，那么 $3$ 个就是可以的；否则我们再尝试 $4$​ 个；如果不是，那么就是 $5$ 个。

证明 $5$​​ 个一定可行：我们考虑因为没有这样的边，所以我们选一条边上的两个点相当于我们选了一条直线的一侧；于是我们选择两条最接近于平行的边，发现在他们没有完全覆盖的一侧再取一个点就可以了。