1 条题解
-
0
自动搬运
来自洛谷,原作者为

Exber
星铁:152282910 | 博客:https://rebxe.github.io/搬运于
2025-08-24 22:36:59,当前版本为作者最后更新于2022-03-16 16:57:53,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
做法
最小割。
这是我第一次在赛场上做出有难度的网络流,写篇题解纪念一下。
赛后发现我的建模方法和官方题解并不相同,所以这篇题解也算是提供了一种新奇的建图思路吧。
首先观察到每个人有两种选择:愿意和不愿意。那么可以用源点表示愿意,汇点表示不愿意。具体就是对第 个人建立节点 ,然后从源点向 连一条流量为 的边,从 向汇点连一条流量为 的边:
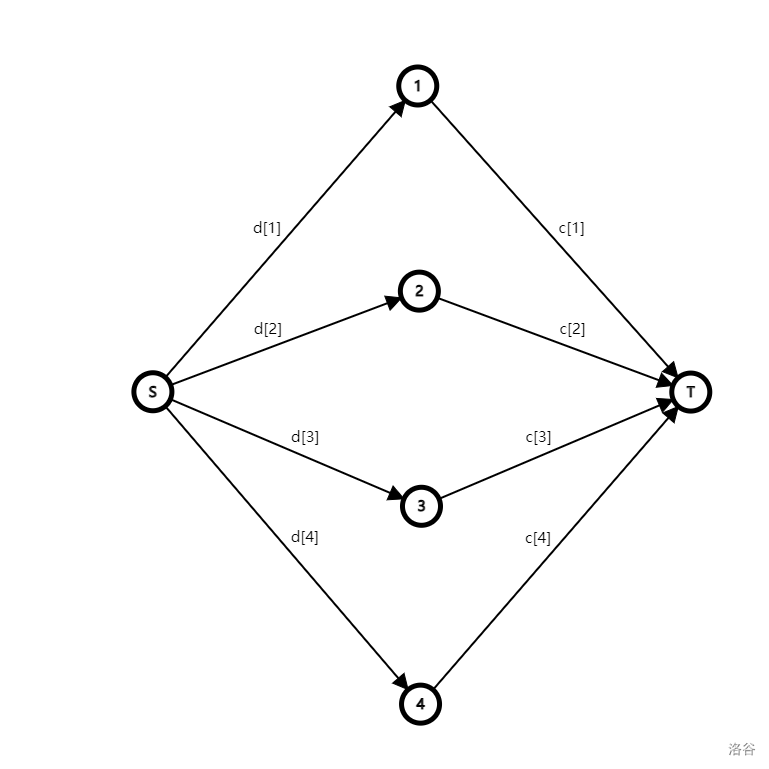
然后考虑同一组内的两个人 意见不同( 选择了愿意)的情况,此时情况如下:
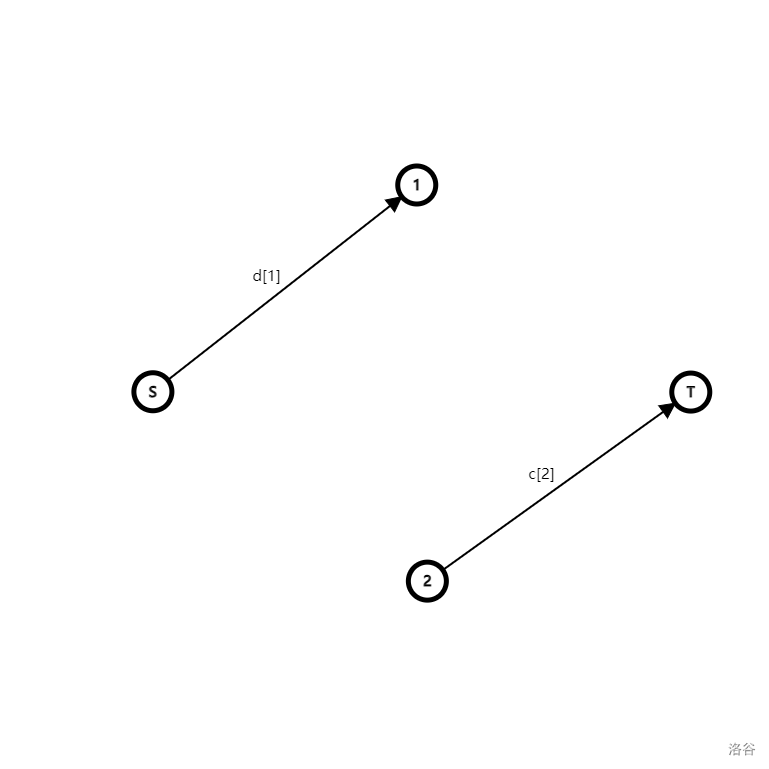
因为会产生 的不满,所以从 向 连一条流量为 的边来增加不满。
对于 选择了愿意但是 选择了不愿意的情况亦然。
加上这些边之后的图如下:(两个奇奇怪怪的点是用来防止边权重叠的)
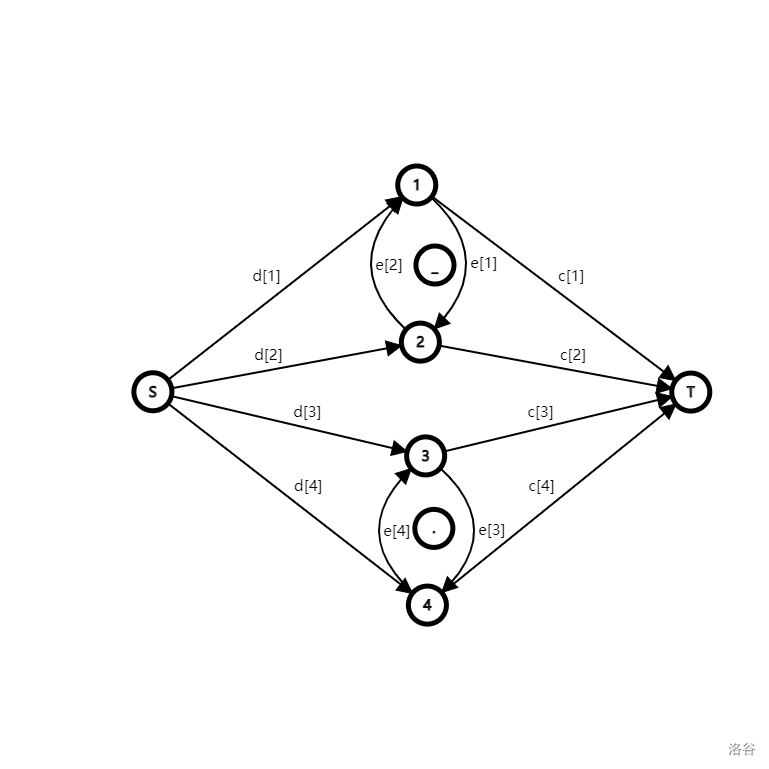
接下来我们就需要解决最棘手的喜欢关系了。(赛场上想了 1h 左右/ll)
首先可以发现,只有一组里两个人都选择愿意才可以合作。所以可以给每一组引入一个点 ,从 分别向两个成员连流量为 的边:
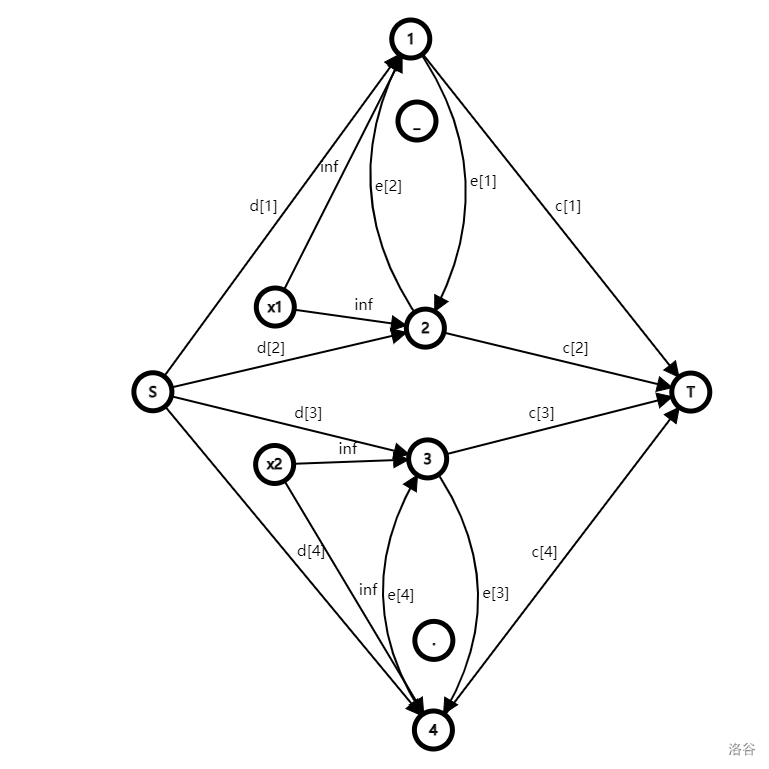
这么连边的目的是,假设有一些流量送到了 :
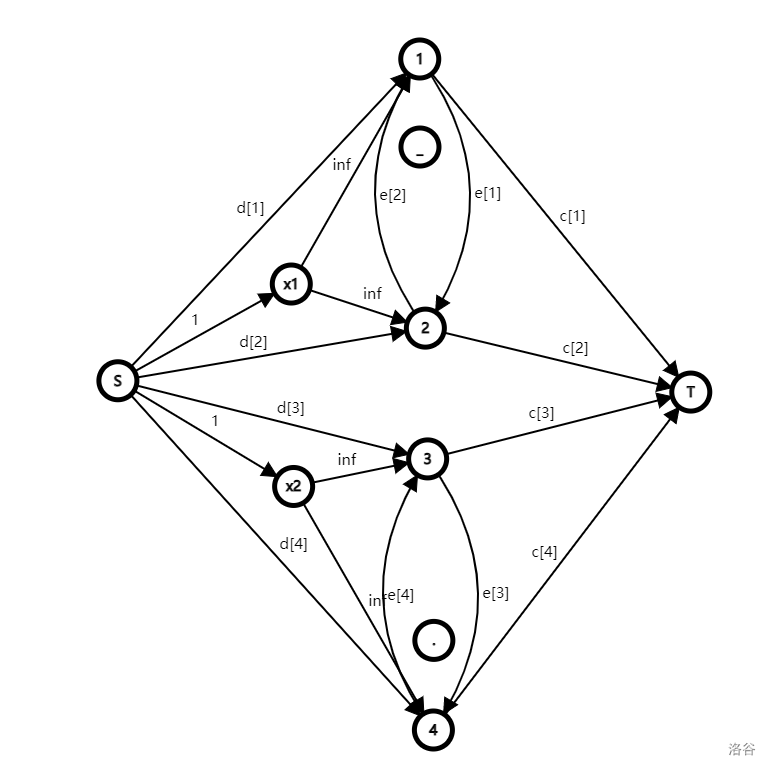
那么就可以保证每一组如果不合作的话给 送流量的边都要被割断,如果合作的话就不隔断,并且如果一组中有一个或以上人选择了不愿意那么就必须不合作。换句话说, 没有流量代表这一组不合作,否则代表这一组合作。
现在我们可以表示合不合作了,接下来考虑喜欢关系的连边。
若第 组关系是 喜欢 ,设 表示 那一组的 , 表示 那一组的 ,那么:
如果 没有和队友合作,并且 选择了愿意,在图上就是 有流量并且 不能有流量。此时会产生 的不满,那么我们可以从有流量的 向不能有流量的 连一条流量为 的边。
如果 选择了不愿意,并且 和队友合作了,在图上就是 连向汇点的边没有被割断并且 有流量。此时会产生 的不满,那么我们可以从有流量的 向可以到达汇点的 连一条流量为 的边。
加上这些边后的图:(假设有一条喜欢关系: 喜欢 )
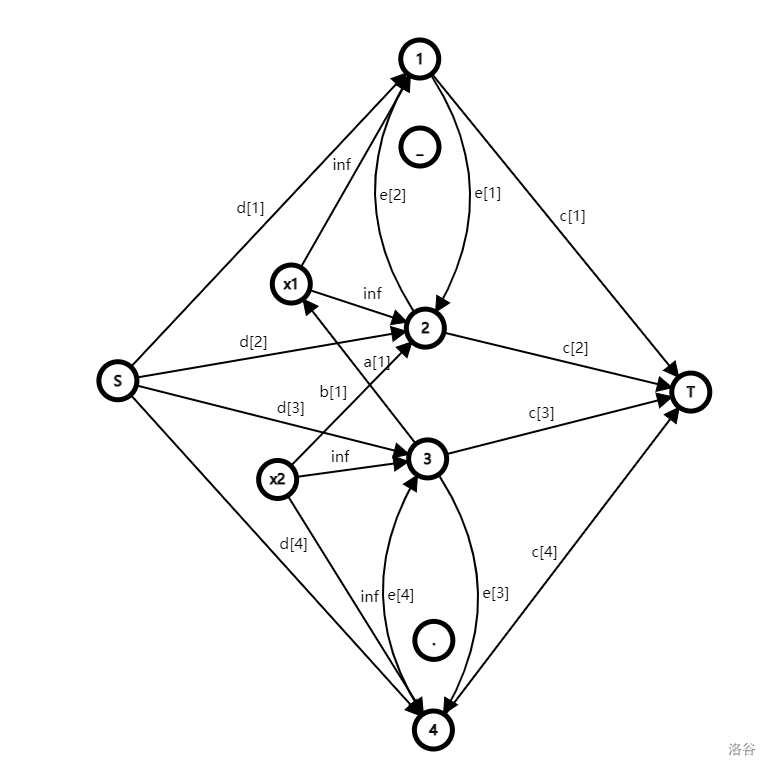
这样我们就建完图了,跑最小割即可。
AC 代码
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> #include <cmath> #include <queue> #include <vector> #include <map> #include <set> using namespace std; struct node { }; typedef long long ll; const ll S=5000005,MS=1000005; int n,m,s,t; int xid[MS]; int esum,to[S],nxt[S],h[MS]; ll c[S]; int dep[MS]; inline void init() { esum=1; memset(h,0,sizeof(h)); s=0; t=1000003; } inline void add(int x,int y,ll w) { c[++esum]=w; to[esum]=y; nxt[esum]=h[x]; h[x]=esum; } inline bool bfs() { memset(dep,0,sizeof(dep)); queue<int> q; q.push(s); dep[s]=1; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=h[u];i;i=nxt[i]) { int v=to[i]; if(c[i]>0&&dep[v]==0) { dep[v]=dep[u]+1; q.push(v); } } } return dep[t]!=0; } ll dfs(int u,ll w) { if(u==t) { return w; } ll sum=0; for(int i=h[u];i;i=nxt[i]) { int v=to[i]; if(c[i]>0&&dep[v]==dep[u]+1) { ll re=dfs(v,min(w,c[i])); c[i]-=re; c[i^1]+=re; sum+=re; w-=re; if(w==0) { break; } } } if(sum==0) { dep[u]=0; } return sum; } inline ll dinic() { ll ans=0; while(bfs()) { ans+=dfs(s,1e17); } return ans; } inline void slove() { scanf("%d%d",&n,&m); n*=2; init(); for(int i=1;i<=n;i++) { ll C,D,E; scanf("%lld%lld%lld",&C,&D,&E); add(s,i,D); add(i,s,0); add(i,t,C); add(t,i,0); int v=(i&1)?i+1:i-1; add(i,v,E); add(v,i,0); } for(int i=1;i<=n;i+=2) { int u=n+(i+1)/2; add(u,i,1e17); add(i,u,0); add(u,i+1,1e17); add(i+1,u,0); xid[i]=u; xid[i+1]=u; } for(int i=1;i<=m;i++) { int x,y; ll a,b; scanf("%d%d%lld%lld",&x,&y,&a,&b); int u1=xid[y],v1=xid[x]; add(u1,x,b); add(x,u1,0); add(y,v1,a); add(v1,y,0); } printf("%lld\n",dinic()); } int main() { int _=1; // scanf("%d",&_); while(_--) { slove(); } return 0; }
- 1
信息
- ID
- 7569
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
