自动搬运

查看原文

来自洛谷，原作者为

	FutaRimeWoawaSete Dear the f**king destiny!

搬运于2025-08-24 22:36:54，当前版本为作者最后更新于2022-03-17 17:00:39，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

每次讲都是脑子会了嘴巴没会，但万幸的是手还会写题解/hanx

场上题都不知道是什么但万幸没开，毕竟我树分块早就忘完了更别说想到了（

不过想到树分块貌似就简单了？

有向邻域的不删除莫队。

先以一般的角度考虑这个问题：这是一道构造题！人畜无害，一点也不数据结构！

观察 $2.5\times 10 ^ 9$，大概是 $n \sqrt m + m\sqrt n$ 的数量级，分块吧。

这里默认大家都会 top cluster 树分块，不会的可以参考 我的博客（不过现在个人觉得讲的不是很好），gxy001 的博客，以及青蛙的集训队论文《浅谈一类树分块的构建算法及其应用》，这里不重点展开。

不过您也可以选择先看完这篇题解之后再去学习 top cluster 树分块，我会把需要的东西都大致讲一下，划分方法可以看完再去学。

简要地讲解一下：top cluster 定义簇为树上的连通块。树分块将一棵树分成了许多个簇，这些簇只有二度簇（可以理解成簇内只有两个端点与其他簇联通），一度簇（簇内只有一个端点与其他簇联通）。

而很显然，簇之间的交只有可能是各自的端点。

并且若设置一个阈值 $B$，该种分法将所有簇的大小控制在 $B$ 以内，将簇的个数控制在 $\frac{6n}{B}$ 之内。

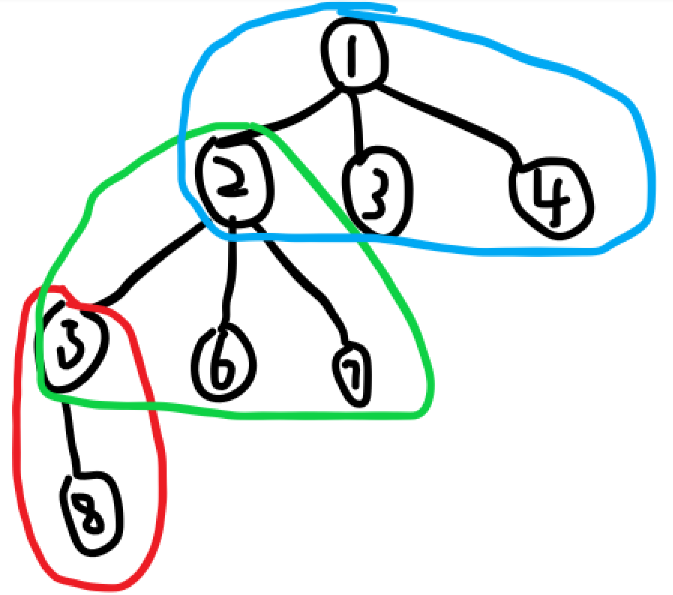
这里给出对样例的树的划分来辅助理解：

其中不同的颜色代表不同的簇。

考虑在进行划分之后，我们对所有的询问 $N(x_i,y_i)$ 进行分类：

• 若 $x_i$ 处于一个二度簇的两个端点的路径上，将这个询问归类为 $1$ 类询问，挂到二度簇里深度较深的端点上；

• 其余的询问都是 $2$ 类询问。

考虑对于 $1$ 类询问，我们对于每个二度簇进行处理。可以先处理出每个节点在根为 $1$ 时的深度，记第 $i$ 个簇深度较深的端点为 $btm_i$，将挂在 $btm_i$ 的所有询问 $N(x_j,y_j)$ 拿出来，按照 $dep_{x_j} + y_j - dep_{btm_i}$ 的大小进行排序。

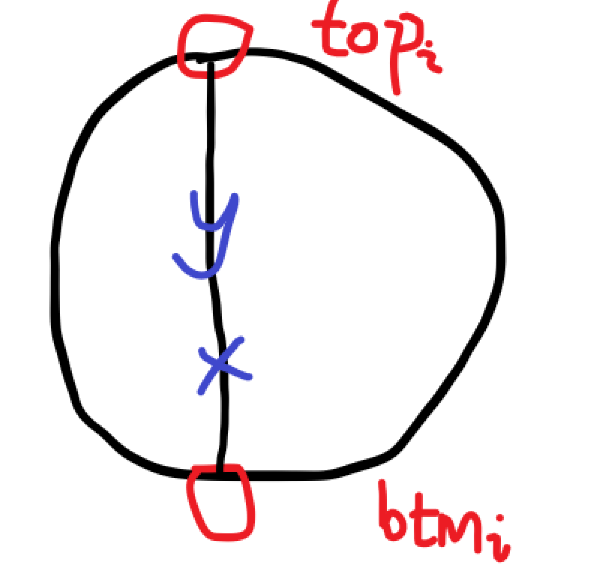
这里再来一张图，就不信看不懂了。

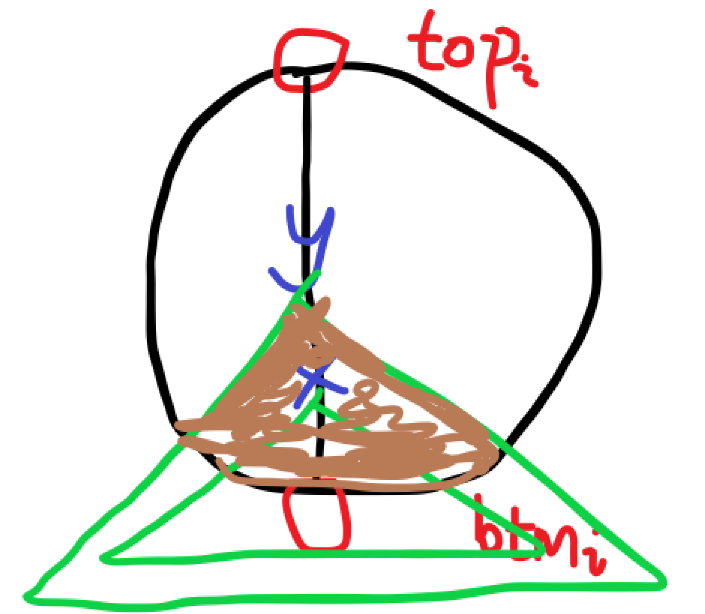
假设排序后询问 $x$ 排在 $y$ 前面：

其中棕色的部分表示两个询问的有向邻域包含的点中，在簇内的部分；未涂色的部分表示不在簇内的部分。

考虑这么构造操作：若当前处理排序后第 $u$ 个询问，记 $V_u = dep_{x_u} + y_u - dep_{btm_i}$，则跳到 $N(btm_i,V_u)$；然后跳到 $N(x_u,y_u)$ 声明后撤回此次跳跃，再跳到下一个 $N(btm_i,V_{u + 1})$ 去处理第 $u + 1$ 个询问；处理完当前簇的所有询问时回到 $N(1,0)$。

我们发现，这样的跳跃在按照 $V_u$ 排序后总是合法的；考虑每次跳跃的代价就是相邻两个有向邻域点量的差异，对于从 $N(btm_i,V_u)$ 跳到 $N(x_u,y_u)$，增加的只会是树簇内的点，即对于每个询问摊一个 $B$ 的代价，若 $1$ 类操作一共有 $m_1$ 个，则此处的贡献代价是 $O(m_1B)$。

对于从 $N(btm_i,V_u)$ 跳到下一个 $N(btm_i,V_{u + 1})$，每次只会向 $btm_i$ 的子树内扩展，对于每个簇的贡献代价不超过 $n$，则此处的贡献代价是 $O(\frac{6n ^ 2}{B})$。

综上，我们证明了对于 $1$ 类询问的总贡献代价不超过 $O(\frac{6n ^ 2}{B} + m_1B)$，操作次数为 $5m_1$。

对于第二类询问，其 $x$ 有可能处于一个一度簇内，有可能处于二度簇的非路径节点上，不过不管 $y$ 怎么变，其有向邻域所能囊括的点都在 $x$ 所在的簇内，其大小不超过 $B$，所以直接跳过去声明后跳回 $N(1,0)$ 就行了，设一共有 $m_2$ 种二类操作，这里的贡献代价不超过 $O(m_2B)$。

综上我们得到了一种贡献代价不超过 $O(\frac{6n^2}{B} + mB)$，操作次数为 $O(5m_1 + 3m_2) \leq O(5m)$ 的方法。细心的读者可能发现对于贡献代价中 $\frac{6n ^ 2}{B}$ 也不是一个完全严格的上界，，因为当 $B$ 一大了块也分不到这么多块，实际操作下来根本卡不到这么多，至于开 $2.5 \times 10 ^ 9$ 不知道是不是就是这种做法的实际严格上界，不过我太菜了还不会完全证明。

最后提一下关于此题的树分块方法。由于我们只用知道每个簇的端点，所以只用记录每个节点下方是否有簇端点，子树内未被划入簇的点数量，当前节点所属簇的 $btm_i$ 即可正确划分。