自动搬运

查看原文

来自洛谷，原作者为

	cff_0102 & aqua_qaq | 团子群 185800038 | 如果我死了说明我 AFO 了

搬运于2025-08-24 22:36:47，当前版本为作者最后更新于2024-10-24 17:17:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目很良心，不需要离散化，但是要开 long long。

看到平面上那么多矩形，首先上一个扫描线。从左往右扫，不难发现碰到的边有一个矩形的左边缘和右边缘两种可能。

先不管矩形的右边缘，假设矩形是无限向右延伸的，看看怎么求出答案。

设 $wcnt$ 是白色块的数量，$bcnt$ 是黑色块的数量。

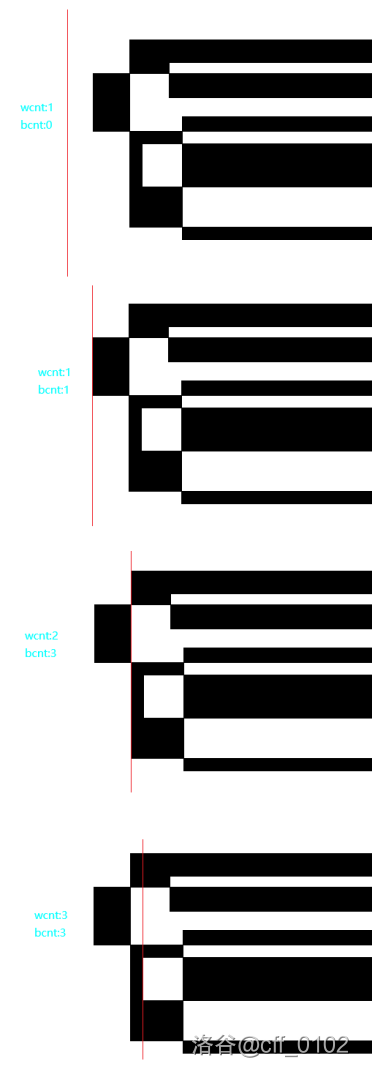
扫描到一个左边缘时，可以知道这条边缘覆盖的范围。它实际上的作用是对扫描线上这段范围的颜色取反，或者说异或了 $1$。但是我们只管答案，可以发现只要知道线扫过去之后右边改变了几块的颜色，就可以对应更新答案。比如上图的扫描线扫到第二个左边缘时，多出现了从上至下的黑、白、黑三块，所以就要将 $bcnt$ 增加 $2$，将 $wcnt$ 增加 $1$。

这一块的实现确实不难。如果这题只考虑左边缘的话也不可能评黑了。

接下来考虑右边缘。先随便画几种情况看看。

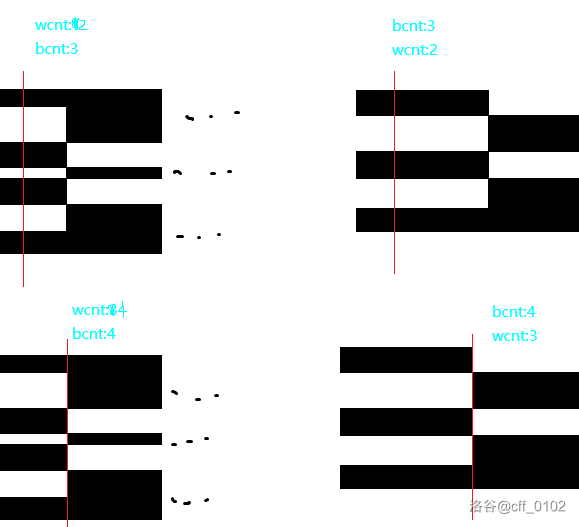
可以发现，在这两种情况中，扫描线经过一个右边缘的时候，原本左边最上面和最下面两块到右边就会“消失”（实际上就是和上方的异色块“合并”了），而中间的其它块会反色且数量保持不变。最终答案应该增加中间的那些色块的数量。

听起来好像没什么问题，但是注意到刚刚说到“上下两块会‘消失’”，那么如果上下在同一块呢？可以直接不处理吗？

这是不行的。考虑下图左边的情况，扫描线扫到下一个右边缘后，上下两边的黑色块“合并”了，导致之前计算为两块的黑色块实际上是一块，所以 $bcnt$ 此时应该自减 $1$。

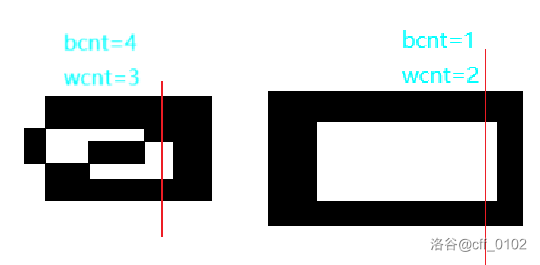
但是再看上图右边的情况，这里扫到右边缘时，又不应该把外面的颜色数量 $-1$，因为它们在前面已经是连在一块的了，这里并没有被当成多块算。

所以什么时候才应该 $-1$ 呢？

扫描线经过当前右边缘，且碰到这种特殊情况时，要将外面颜色的颜色数量 $-1$，当且仅当这个右边缘上下两块先前被当成了两块。不难发现，如果当前扫过的矩形和外面那块的矩形边界连通，才会导致外面的矩形的这两个部分在扫描线扫过里面这个矩形的右边缘之前一直被当做是两块（因为，如果中间不连通，断开了，那么在断开的那个时候上下两块就已经被连接在一起了，此时并没有被当成是不同的两块）。所以，在扫到右边缘且碰到这种特殊情况时，只需要判断当前右边缘所在的矩形与它外面（上方、下方、右侧）的那个矩形（如果有的话），边界是否连通即可。如果连通，再将对应颜色的答案 $-1$。

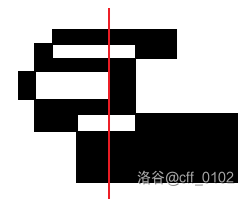
说起来倒容易，但实际上应该怎么确定外面的那个矩形是几号呢（比如上图的情况）？实际上并不需要这样做，每次碰到右边缘的这种特殊情况就直接将外面的这个 $-1$ 即可。减多了怎么办？加回去就行了。注意到每次减多的时候，里面的这个矩形和外面的不连通，即这是另一个连通块。考虑一整个连通块，这个连通块外侧的颜色必然是相同的。假设这个连通块的某个右边缘“减多了”。首先这个右边缘必然在最外侧（如果在内侧就不是“减多了”），所以被减多的颜色应该是这整个连通块外面的颜色。显然，这个颜色在第一次扫到这个连通块时就能得到。在每次扫到一个新的连通块时将外面那个颜色答案直接 $+1$ 就可以避免被多减的情况了。至于为什么只会被多减一次，既然拿一个一维的扫描线去扫这个二维的平面，是不可能在中间把外面的区域分成三份还让它们都在某个右边缘合并消失的，除非这不止一个连通块。

至于如何判断连通块嘛，提前再拿一个扫描线扫一遍，用并查集合并就可以了。

两次扫描可以使用一棵线段树实现：

• 线段树的节点维护当前区间内存在的所有横边的位置。
• 第一次扫描时，每次碰到一个竖边，把它与它覆盖的所有横边对应的矩形合并：
  • 每个区间有一个标记 $tag$。如果这个区间内部没有被访问和修改，这个标记保持不变。
  • 假设当前线段树节点对应的区间是 $[nl,nr]$，要与编号为 $rect$ 的矩形合并的区间是 $[ml,mr]$，且 $[nl,nr]\in[ml,mr]$，即现在这一整个区间里的所有横边对应的矩形都需要与 $rect$ 合并。那么：
    • 若当前区间 $tag=0$，直接将 $tag$ 修改为 $rect$。在这之后要删除里面的一条横边时会将 $tag$ 下传，所以不用担心 $rect$ 最终不能合并到这个区间的所有矩形。
    • 否则，说明还有一个矩形同时也要和当前区间的所有矩形合并，那么直接将并查集的 $tag$ 和 $rect$ 合并即可，在以后 $tag$ 会带着 $rect$ 与这段区间中的矩形合并的。
  • 这样就能成功把所有连通块使用并查集正确合并。
  • 这部分需要注意，如果一个区间里面本来就没有横边，即 $sum=0$，那么 $rect$ 不需要和这个区间的任何矩形合并，也就不需要修改 $tag$。
• 第二次扫描时，要知道一块的颜色，可以转化成求这里到最外面要经过的矩形边缘数量，因此可以通过求解当前 $[1,x]$ 中横边的数量来得到当前这一块的颜色。接下来按照前面所说的方法实现，注意一些细节问题，其它就没什么了。具体可以参照代码。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n;
struct uf{
	int fa[N];
	void setup(){
		for(int i=1;i<=n;i++)fa[i]=i;
	}
	int find(int x){
		if(x==fa[x])return x;
		return fa[x]=find(fa[x]);
	}
	void merge(int x,int y){
		fa[find(x)]=find(y);
	}
}rec;
struct segtree{
	struct node{
		int l,r;
		int sum,tag;
	}a[N<<4];
	#define lc(x) (x<<1)
	#define rc(x) ((x<<1)|1)
	void build(int p,int l,int r){
		a[p].l=l,a[p].r=r;
		if(l==r)return;
		int mid=(l+r)>>1;
		build(lc(p),l,mid);
		build(rc(p),mid+1,r);
	}
	void pd(int p){
		if(!a[p].tag)return;
		int tag=a[p].tag;
		a[p].tag=0;
		if(a[lc(p)].sum){
			if(!a[lc(p)].tag)a[lc(p)].tag=tag;
			else rec.merge(a[lc(p)].tag,tag);
		}
		if(a[rc(p)].sum){
			if(!a[rc(p)].tag)a[rc(p)].tag=tag;
			else rec.merge(a[rc(p)].tag,tag);
		}
	}
	void pu(int p){
		a[p].sum=a[lc(p)].sum+a[rc(p)].sum;
	}
	void add(int p,int ad,int x){
		int l=a[p].l,r=a[p].r;
		if(r<ad||l>ad)return;
		if(l==r){
			a[p].sum+=x;
			//不用打 tag，因为这里先前已经被 merge 到了
			return;
		}
		pd(p);
		add(lc(p),ad,x);
		add(rc(p),ad,x);
		pu(p);
	}
	void merge(int p,int ml,int mr,int rect){
		int nl=a[p].l,nr=a[p].r;
		if(nr<ml||nl>mr)return;
		if(nl>=ml&&nr<=mr){
			if(!a[p].sum)return;
			if(!a[p].tag)a[p].tag=rect;
			else rec.merge(rect,a[p].tag);
			return;
		}
		pd(p);
		merge(lc(p),ml,mr,rect);
		merge(rc(p),ml,mr,rect);
		//pu(p);其实不需要 
	}
	int sum(int p,int sr){
		int nl=a[p].l,nr=a[p].r;
		if(nl>sr)return 0;
		if(nr<=sr)return a[p].sum;
		return sum(lc(p),sr)+sum(rc(p),sr); 
	} 
}st;
struct line{
	int yd,yu;
	int rect;
	bool in;
}l[N];//垂直线段
bool vis[N];
signed main(){
	ios::sync_with_stdio(0);cin.tie(0);
	int t;cin>>n>>t;
	for(int i=1;i<=n;i++){
		int xa,xb,ya,yb;cin>>xa>>ya>>xb>>yb;
		l[xa]={ya,yb,i,1};
		l[xb]={ya,yb,i,0};
	}
	rec.setup();
	st.build(1,1,n<<1);
	for(int i=1;i<=(n<<1);i++){
		int yu=l[i].yu,yd=l[i].yd;
		st.merge(1,yd,yu,l[i].rect);
		if(l[i].in){
			st.add(1,yd,1);
			st.add(1,yu,1);
		}else{
			st.add(1,yd,-1);
			st.add(1,yu,-1);
		}
	}
	int wcnt=1,bcnt=0;
	for(int i=1;i<=(n<<1);i++){
		if(l[i].in){
			//加边
			int d=st.sum(1,l[i].yd),u=st.sum(1,l[i].yu);
			int ch=u-d+1;//改变了几块的颜色
			bool col=d%2;//最下面的颜色（1 黑 0 白）
			if(!vis[rec.find(l[i].rect)]){//这是一个新的连通块！
				vis[rec.find(l[i].rect)]=1;
				if(col)bcnt++;
				else wcnt++;
			}
			if(col){
				//从下到上：白黑白黑……
				wcnt+=(ch+1)/2;
				bcnt+=ch/2;
			}else{
				//从下到上：黑白黑白……
				bcnt+=(ch+1)/2;
				wcnt+=ch/2;
			}
			st.add(1,l[i].yd,1);st.add(1,l[i].yu,1);
		}else{
			//删边
			st.add(1,l[i].yd,-1);st.add(1,l[i].yu,-1);
			int d=st.sum(1,l[i].yd),u=st.sum(1,l[i].yu);
			int ch=u-d-1;//改变了几块的颜色
			bool col=d%2;//最下面的颜色（1 黑 0 白）
			if(u==d){//特殊情况
				//if(rec.find(l[i].rect)==rec.find(/*外侧那个矩形的编号*/))
				//不管，直接减
				if(col)bcnt--;
				else wcnt--;
			}else{
				if(col){
					wcnt+=(ch+1)/2;
					bcnt+=ch/2;
				}else{
					bcnt+=(ch+1)/2;
					wcnt+=ch/2;
				}
			}
		}
	}
	if(t==1)cout<<wcnt+bcnt;
	else cout<<wcnt<<" "<<bcnt;
	return 0;
}