自动搬运

查看原文

来自洛谷，原作者为

	unputdownable 下雨不是任何人的错。

搬运于2025-08-24 22:36:40，当前版本为作者最后更新于2022-02-26 22:38:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

考虑如何求出 $J_m(n)$。

递归，如果 $n < m$，$J_m(n)=1$；

如果 $n \geq m$，考虑报一遍 $1-m$：

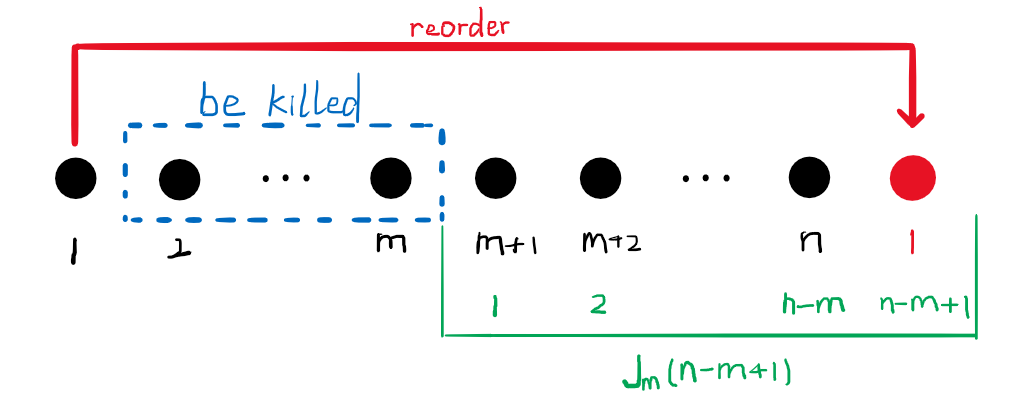
所以有：

$$J_m(n)=\begin{cases}1 & J_m(n-m+1)=n-m+1\\J_m(n-m+1)+m & \text{else}\end{cases} $$

于是可以将 $n$ 按模 $m-1$ 分类，这样在每一类中，除了若干个 $J_m(n)=n$ 的位置外，都是公差为 $m$ 的等差数列。

---

考虑每一类中有哪些不满足等差的位置（下称断点）。

由于 $J_m(n)=n$ 的下一项必然是 $1$，所以一个 $1$ 对应一个断点。

思考 $J_m(n)$ 什么情况下为 $1$：

上面提过 $1 \leq n < m$ 的时候是 $1$；

当 $n \geq m$ 时，易得 $n$ 必然是 $m$ 的倍数，否则报完一圈后 $1$ 一定当场出局，于是除 $m$ 后归纳。

可得断点只有 $k \times m^a$ 的形式，其中 $1 \leq k \leq m-1$。

那么每个同余类中就只有 $\log$ 个断点（$k \times m^a$ 正好在 $k$ 这个同余类中），拆成 $\log$ 个等差数列分别求和即可。

这样就得到了一个 $\Theta(m\log_m a)$ 的算法。

对于每一个 $i$ 暴力找出其前面最后一个断点，就能得到一个 $\Theta(\log_m a)$ 的单点求值算法。

两者结合起来可以得到 $55$ 分的好成绩。

---

继续观察第 $k$ 组的答案。

事实上断点是 $k \times m^a$ 的形式，而点的个数是 $\lfloor \frac{n-k}{m-1}+1 \rfloor$。

只要断点的个数相同，并且点的个数相同，那么可以发现答案就是关于 $k$ 的不超过 $2$ 次的多项式。而断点个数和点的个数都只有两种，所以按这个把要算的东西分成三段，对每一段插值算即可。

时间复杂度 $\Theta(\log_m a)$。