自动搬运

查看原文

来自洛谷，原作者为

	Licykoc 红雨漂泊泛起了回忆怎么潜

搬运于2025-08-24 22:36:33，当前版本为作者最后更新于2022-11-08 08:22:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

reference： eJOI2021 Day1 Editorial

$n = 1$ 部分分是本题关健。

可以猜测此时可行的最优解是 $2^m - 1$，考虑构造。

• 如果 $m = 2^k (k \in \mathbb N_+)$，那么可以构造出 $\forall 0 \le i \le n - 1, a_i \gets i \oplus (i >> 1)$。这其实就是格雷码，其一性质就是可任意 rotate。

• 否则将 $m$ 拆成 $2^{k_1} + 2^{k_2} + \cdots +2^{k_p},(k_1\gt k_2 \gt \cdots \gt k_p)$，单个 $2^{k_i}$ 按照上述做法构造，同时其中每个元素要加上 $2 ^ {k_1} + \cdots + 2^{k_{i-1}}$，这样就能保证没有重复元素。接下来需要合并。

• 令 $i = p \to 2$，当前合并到 $2^{k_i}$ 和 $2^{k_{i-1}}$。可以观察到，$2^{k_{i-1}}$中一定有一个数与 $2^{k_i}$ 第一个数满足条件，所以将 $2^{k_{i-1}}$ 中那个数 rotate 到末尾即可。容易证明这样构造是对的。

• 称以这种方式构造出来的序列为 CompactGrayCode。

对于 $n \gt 1$ 时，分别构造 $n,m$ 所对应的 CompactGrayCode，记为 CGCn 和 CGCm。对于每个 $a_{i, j}$，都以二进制下的某种方式拼接 CGCn[i] 和 CGCm[j]，得到一组可行解。这样的正确性显然，问题也就变成了找到最小代价的拼接方式。

这里用 $n = m = 6$ 来加以说明。首先，CGCn 和 CGCm 均为：

$$5 = 101_{2}, 1 = 001_{2}, 3 = 011_{2}, 2 = 010_{2}, 0 = 000_{2}, 4 = 100_{2} $$

如果选择顺次拼接，那么矩阵如下图：

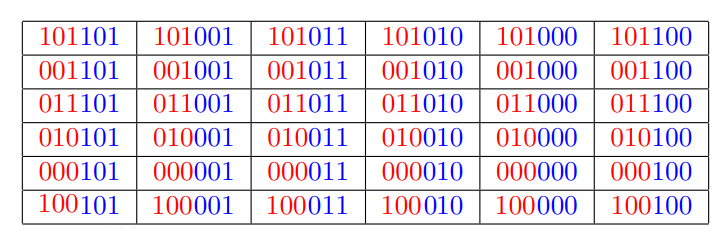
可以发现最大值为 $45 = \textcolor{red}{101}\textcolor{blue}{101}_2$。

但如果以下图拼接，

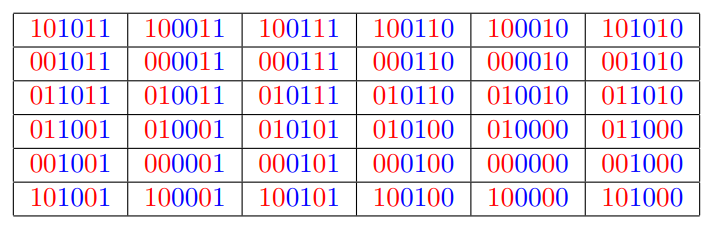
最大值仅为 $43 = \textcolor{red}{10}\textcolor{blue}{10}\textcolor{red}1\textcolor{blue}{1}_2$

发现最大值只跟 CGCn 和 CGCm 中的最大值有关，于是可以 dp 求解。

$f_{i, j}$ 表示取了 CGCn 最大值的前 $i$ 位，CGCm 最大值的前 $j$ 位，拼接成的最小值。

dp 后构造方案是容易的。

参考实现：

#include <bits/stdc++.h>

signed main () {
  std::ios::sync_with_stdio(false);
  std::cin.tie(nullptr);

  int n, m;
  std::cin >> n >> m;

  std::vector<std::vector<int>> Gray(11);
  for (int i = 0; i <= 10; ++i) {
    for (int j = 0; j < (1 << i); ++j) {
      Gray[i].emplace_back(j ^ (j >> 1));
    }
  }

  auto GetCompactGray = [&](int x) {
    std::vector<std::vector<int>> tmp;
    for (int i = 10; ~i; --i) {
      if (x >> i & 1) {
        tmp.emplace_back(Gray[i]);
      }
    }

    int lim = 0;
    for (auto &i : tmp) {
      for (auto &j : i) {
        j += lim;
      }
      lim += i.size();
    }

    for (int i = (int)tmp.size() - 1; i; --i) {
      auto &l = tmp[i - 1], &r = tmp[i];
      for (int j = 0; j < (int)l.size(); ++j) {
        if (__builtin_popcount((l[j] ^ r[0])) == 1) {
          rotate(l.begin(), l.begin() + j + 1, l.end());
          break;
        }
      }
    }

    std::vector<int> res;
    for (auto &i : tmp) {
      res.insert(res.end(), i.begin(), i.end());
    }

    return res;
  };

  auto CompactGrayn = GetCompactGray(n--), CompactGraym = GetCompactGray(m--);
  int x = (!n) ? 1 : std::__lg(n) + 1, y = (!m) ? 1 : std::__lg(m) + 1, all = x + y - 1;
  std::vector<std::vector<int>> f(x + 1, std::vector<int>(y + 1, (1 << 11))), pre(f);

  f[0][0] = 0;
  for (int i = 1; i <= x; ++i) {
    f[i][0] = f[i - 1][0] | ((n >> (x - i) & 1) << (all - i + 1));
    pre[i][0] = 1;
  }
  for (int i = 1; i <= y; ++i) {
    f[0][i] = f[0][i - 1] | ((m >> (y - i) & 1) << (all - i + 1));
    pre[0][i] = 2;
  }
  for (int i = 1; i <= x; ++i) {
    for (int j = 1; j <= y; ++j) {
      int I = f[i - 1][j] | ((n >> (x - i) & 1) << (all - i - j + 1)), J = f[i][j - 1] | ((m >> (y - j) & 1) << (all - i - j + 1));
      if (I < J) {
        f[i][j] = I;
        pre[i][j] = 1;
      } else {
        f[i][j] = J;
        pre[i][j] = 2;
      }
    }
  }

  std::vector<int> from(x + y);
  int now = 0;
  for (; x || y; ) {
    from[now++] = pre[x][y];
    if (pre[x][y] == 1) {
      --x;
    } else {
      --y;
    }
  }

  for (int i = 0; i <= n; ++i) {
    for (int j = 0; j <= m; ++j) {
      //merge CompactGrayn[i] and CompactGraym[j]
      int res = 0, x = CompactGrayn[i], y = CompactGraym[j];
      for (int k = 0; k < now; ++k) {
        if (from[k] == 1) {
          res |= (x & 1) << k;
          x >>= 1;
        } else {
          res |= (y & 1) << k;
          y >>= 1;
        }
      }
      std::cout << res << " \n"[j == m];
    }
  }
}