1 条题解
-
0
自动搬运
来自洛谷,原作者为

jjsnam
I'm no good at goodbyes.搬运于
2025-08-24 22:36:31,当前版本为作者最后更新于2022-04-21 22:24:27,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
写在前面
最近在学倍增,被紫题虐哭后又来尝试这个蓝题,没想到实现起来也有一定的难度。 看不懂大佬们的题解和代码,所以打算写一个比较易懂的题解。
其实思路与第一篇题解类似,但是它讲的太笼统了。就像 "经" 需要 "传" 来解释一样,所以我打算将这种思路写的更详细一些,让有一定倍增基础的同志们可以看懂。
前置知识
- 线段树
- 单调队列
- 倍增
题目大意(戳这里查看原题)
- 给定 个点, 条路线。
- 给定一个整数 ,表示乘车点离始发点的最远距离。
- 对于每条路线,给定 表示路线的起点和终点。
注意: , 相对大小关系不确定,可分别表示正向和反向。 - 接下来有 次询问。
- 对于每次询问,给定 表示询问的起点和终点。求是否能够通过换乘从 到达 ,如果可以输出最少换乘次数。
- 无解输出 。
正文
就我目前的经验来看,凡是需要多次无序询问或者重复多次处理一张图时,大概率是需要用到倍增的。
简单说一下原因:当我们要多次处理(或询问)一张图时(假设 个点),那么如果一次次遍历,复杂度很可能是 或更高,在动不动就 的数据下肯定是不行的,而倍增可以将每次遍历降到 级别,显然是一种很有效的优化方法。
然后我们以倍增作为思考切入点,再回到这题。我们可以先把数据(样例 3)
手出来观察一下: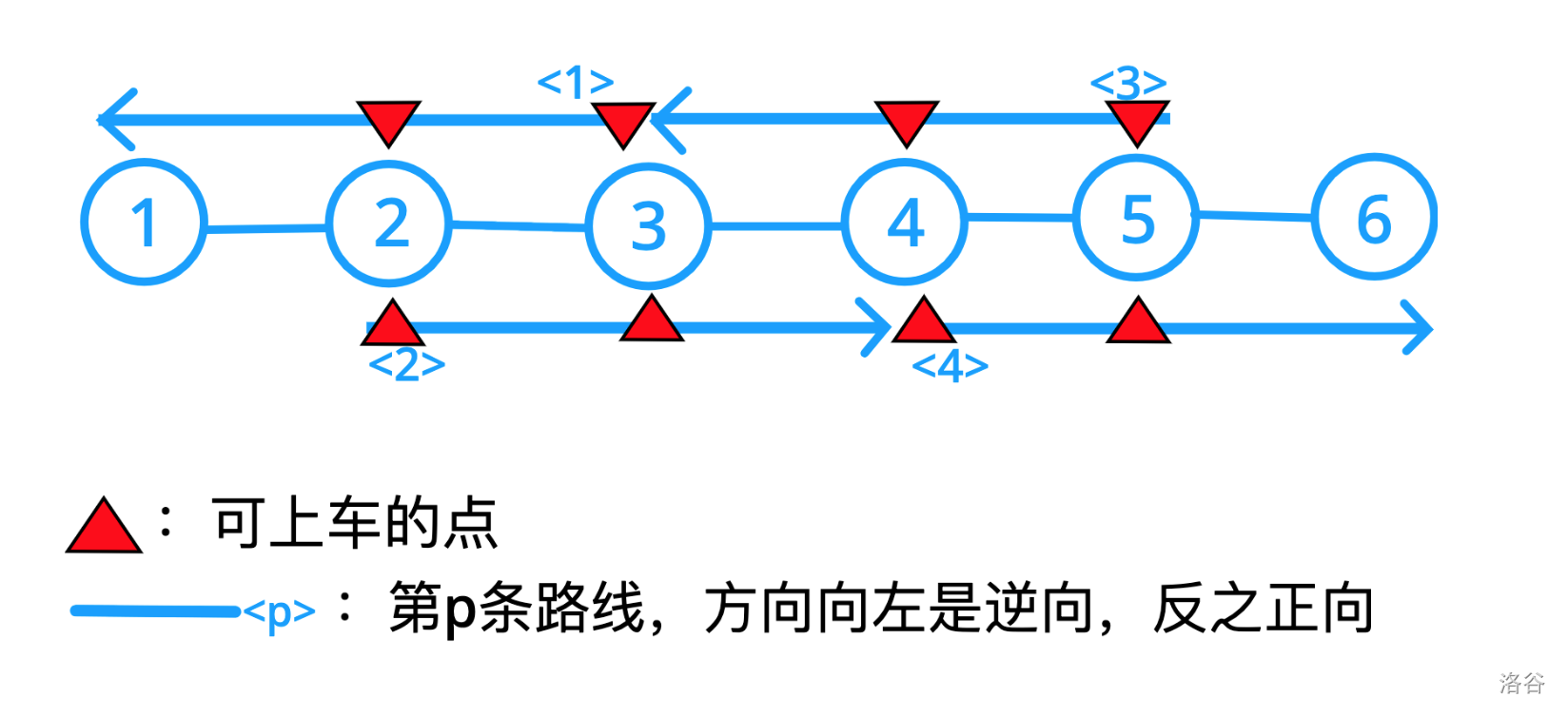
以 , 为例, 我们要从 号点走到 号点,则需要在 号点坐二号线于 号点下车,再从 号点坐四号线于 号点下车。需要坐 条线路。
一看就非常想上倍增。满足多次无序询问,而且这个图很大,但是感觉又不老好实现的,我们继续思考。
接下来从倍增两个基本步骤入手:预处理、询问。
预处理
考虑倍增。终点可以在起点的左边,也可以在起点的右边。所以左右都要考虑到。我们用 、 分别代表以第 个点为起点,乘坐 条路线所能到达的最远左端点、右端点。
可以证明:此时第 点乘坐 条路线能到达的所有点均属于区间 ,且该区间内没有点不能被 到达。(可以这么想:既然能到达最远,则一定有一条路线连接起点和最远点,那么中间的这些点只要提前下车就行了。上车有限制,但是下车没有)。
接下来想一下如何递推倍增式。对于 次换乘,一定保证 且 才有意义。通过我们刚才的推论,在 中的所有点都可以被 点到达,则我们可以在 乘坐一条路线时选择到达其中的一点 ,通过 的 和 来扩展点 的情况。式子就很容易得出了:
;
;
其中 。
考虑一般情况: 显然递推要使用一个区间内的最值,这就成为了一个 RMQ 问题,那么一个个枚举显然是很耗时的。 我们可以用线段树来优化这个过程。 (之后,我们可以想想是用一颗线段树滚动,还是要建很多颗线段树 ? )
现在还有一个很
棘手的问题,就是初始的 , 如何得出? 我是没想出如何用线段树, 但我们可以使用一个稍加修改的单调队列求出。(正是别的题解对这块一笔带过才让我下决心写这篇题解)现在考虑单调队列,首先,队列要装路线(这样处理出终点最远的路线,计算答案时找到这个终点即可),所以大小应该是 个。其次,需要改动的地方就是我们要在枚举路线的同时更新我们的点。 这个想想应该也能明白,我们枚举每个点,同时以这个点为参照逐渐枚举路线。
以求 为例,即在队列里的路线满足起点在该点前,终点在该点后,队列中路线的终点要最右,所以这些路线按照其终点的大小在队列中满足单调递减。
注意:我们如果要枚举到满足这个点条件的所有路线,显然要将这些路线按起点排序。
还有两个小细节:
-
是向右最远的点,所以只有正向路线可能有影响;反之 则只受逆向路线影响。要分开枚举。
-
单调队列中,如何判断一条路线是否合法?以求 为例。对于一个路线的起点 ,合法满足 , 整理得 ,则对于任意 的路线都不能满足 是起点,是不合法的,应该删去。
则预处理的总复杂度 。
分别是一般情况的线段树倍增和起始的单调队列。
询问
然后这题的难点就基本解决了。我们再来考虑一下询问如何处理。
对于一对询问 ,我们尝试从 不断向左右扩展,直到能到达的区间覆盖住了 。
同时注意一下如何保证正确性:
可以联想一下倍增求 LCA。首先我们要倒序枚举 保证大的先处理。 同时,LCA 在处理的时候不会让两个点跳到一起,只会跳到最近公共祖先的子节点,从而保证不会出现跳到 LCA 上面导致祖先重合的情况。 类比这个方法, 我们也可以使最后的区间 将要但不包括 ,从而避免乘坐了过多的线路。
最后我们再来考虑一下最终的答案:
对于一次询问,我们为了保证正确性,确保每次更新换乘点都满足不达到,但尽可能将要到达终点。那么当我们完成一次完整的循环处理(即从换乘 次一直到换乘 次后到达的点),这时记录的答案一定不能够使我们到达终点。可以证明,如果这个询问有解,当且仅当终点 位于最后一次到达的换乘点 换乘一次可到达的点的范围内()。若不满足这个条件则无解,输出 。
如果读者不明白为什么是这个条件,我们仍然可以联想倍增求 LCA。这里我通过反证法给出一个不严谨的简单证明:
假如最后的终点 不满足上面的条件且保证有解,则一定满足 ,其中 。然而,我们在处理询问的循环中是从大到小枚举 ,则一定可以找到一个枚举的 ,将最后的换乘点 更新,且满足不达到,但将要到达终点这个条件。前后矛盾。
注意: 按照这种方法扩展也不能只考虑起点,而是要考虑每次换乘起点所能到达的所有点,取最优。然后又回到了令人
欣喜的 RMQ 环节。我们直接枚举倍增的数组显然也不是最优的,这就突显出我们线段树的好处了,自然我们可以用处理倍增的线段树来在 下得出当前的最优。也就回答了上面的思考,我们要建 颗线段树,不用滚动优化。
询问的复杂度 。
最后的总复杂度 。
代码
对一些变量名的解释(
我觉得是比较正常的)-
表示向左最远到达点的倍增数组
-
表示向右最远到达点的倍增数组
-
, 用于记录正向路径(取 上行意)
-
, 用于记录逆向路径(取 下行意)
因为要建多颗线段树,所以用结构体封装,开 个线段树。
/* code by jjsnam 2022.4.29 */ /* Using Segment Tree */ #include <iostream> #include <algorithm> #include <cstring> #define ls (id<<1) #define rs (id<<1|1) #define mid ((l+r)>>1) #define u first #define v second using namespace std; typedef pair<int,int> pii; const int maxn=1e5+5; const int maxm=2e5+5; int le[maxn][17],ri[maxn][17]; pii up[maxm],down[maxm]; int cnt_up,cnt_down; int n,m,K,Q; struct Segment_Tree{ struct Node{ int left,right; }tr[maxn<<2]; void pushup(int id){ tr[id].left=min(tr[ls].left,tr[rs].left); tr[id].right=max(tr[ls].right,tr[rs].right); } void build(int id,int l,int r,int k){ if (l==r){ tr[id].left=le[l][k]; tr[id].right=ri[r][k]; return; } build(ls,l,mid,k); build(rs,mid+1,r,k); pushup(id); } int query_left(int id,int l,int r,int a,int b){ if (a<=l&&r<=b){ return tr[id].left; } int res=1e9; if (a<=mid) res=min(res,query_left(ls,l,mid,a,b)); if (b>mid) res=min(res,query_left(rs,mid+1,r,a,b)); return res; } int query_right(int id,int l,int r,int a,int b){ if (a<=l&&r<=b){ return tr[id].right; } int res=-1e9; if (a<=mid) res=max(res,query_right(ls,l,mid,a,b)); if (b>mid) res=max(res,query_right(rs,mid+1,r,a,b)); return res; } }root[17]; void Get_start(){ for (int i=1;i<=n;i++) le[i][0]=ri[i][0]=i; sort(up+1,up+cnt_up+1); sort(down+1,down+cnt_down+1,greater<pii>()); /* 单调队列 O(m) */ int q[maxm],hh=1,tt=0; /* 处理右 */ for (int i=1,j=1;i<=n;i++){ while (j<=cnt_up&&up[j].u<=i){ int r=up[j].v; while (hh<=tt&&up[q[tt]].v<=r) tt--; q[++tt]=j; j++; } while (hh<=tt&&up[q[hh]].u<=i-K) hh++; if (hh<=tt) ri[i][0]=max(ri[i][0],up[q[hh]].v); } /* init */ hh=1,tt=0; /* 处理左 */ for (int i=n,j=1;i>0;i--){ while (j<=cnt_down&&down[j].u>=i){ int l=down[j].v; while (hh<=tt&&down[q[tt]].v>=l) tt--; q[++tt]=j; j++; } while (hh<=tt&&down[q[hh]].u>=i+K) hh++; if (hh<=tt) le[i][0]=min(le[i][0],down[q[hh]].v); } } void init(){ Get_start(); root[0].build(1,1,n,0); for (int k=1;k<=16;k++){ for (int i=1;i<=n;i++){ le[i][k]=root[k-1].query_left(1,1,n,le[i][k-1],ri[i][k-1]); ri[i][k]=root[k-1].query_right(1,1,n,le[i][k-1],ri[i][k-1]); } root[k].build(1,1,n,k); } } int query(int S,int E){ int res=0; int l=S,r=S; for (int k=16;k>=0;k--){ int L=root[k].query_left(1,1,n,l,r); int R=root[k].query_right(1,1,n,l,r); if (L<=E&&E<=R) continue; l=L,r=R; res+=(1<<k); } int L=root[0].query_left(1,1,n,l,r); int R=root[0].query_right(1,1,n,l,r); if (L<=E&&E<=R) return res+1; else return -1; } int main(){ ios::sync_with_stdio(false); cin.tie(0),cout.tie(0); cin >> n >> K >> m; for (int i=1,a,b;i<=m;i++){ cin >> a >> b; if (a<b) up[++cnt_up]=make_pair(a,b); else down[++cnt_down]=make_pair(a,b); } init(); cin >> Q; int s,e; while (Q--){ cin >> s >> e; cout << query(s,e) << endl; } return 0; }
总结
此题的这种做法其实是 RMQ 问题与倍增的结合。
它与其他倍增题做法有一些不同之处:
-
最后询问不是直接使用倍增数组,而是用更新倍增数组的线段树更新答案。
可以这么理解:每一层倍增由上一层的线段树区间最值求得,而这一层的线段树初始值则是更新后的倍增数组。所以广义上说,我们存的线段树也算一个倍增。 -
本题更新倍增数组的方法也不是单一的递推,而是通过线段树优化后的区间最值递推。
然后这道题就结束了!好耶(
应该还是有更优的 RMQ 做法的,但是我太弱了想不出来(
第一次写题解,可能我的表述也比较菜,如果有问题欢迎指出!
- 1
信息
- ID
- 7498
- 时间
- 2000ms
- 内存
- 537MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
