1 条题解

  • 0
    @ 2025-8-24 22:36:19

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar warzone
    梦违科学世纪

    搬运于2025-08-24 22:36:19，当前版本为作者最后更新于2022-03-11 15:30:49，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    题目大意

    你在一个 dd 维空间中。

    给出空间中 nn 个点的坐标 y⃗1,y⃗2,⋯ ,y⃗n\vec{y}_1,\vec{y}_2,\cdots,\vec{y}_n 及它们与你的距离 r1,r2,⋯ ,rnr_1,r_2,\cdots,r_n，

    请你求出你所在的坐标 x⃗\vec{x}。

    若有多个解，输出任意一个。

    Data Range:1≤n,d≤500\texttt{Data Range}:1\le n,d\le 500，坐标范围 [−100,100][-100,100]，保证数据随机且有解。

    题解

    给出一个 naive 的数形结合的做法。

    根据题意，不难列出方程

    $$\begin{cases} (\vec{x}-\vec{y}_1)^2=r_1^2\\ (\vec{x}-\vec{y}_2)^2=r_2^2\\ \cdots \\ (\vec{x}-\vec{y}_n)^2=r_n^2 \end{cases} $$

    这个方程含有平方，所以没法直接高斯消元。

    但注意到

    $$(\vec{x}-\vec{y})^2=\vec{x}^2-2\vec{y}\cdot\vec{x}+\vec{y}^2 $$

    其中 x⃗2\vec{x}^2 是相同的。

    考虑将原点平移到 y⃗1\vec{y}_1，设 $\vec{x}'=\vec{x}-\vec{y}_1,\forall k,\vec{y}_k'=\vec{y}_k-\vec{y}_1$，则

    $$\begin{cases} \vec{x}'^2=r_1^2&(1)\\ (\vec{x}'-\vec{y}_2')^2=r_2^2\\ (\vec{x}'-\vec{y}_3')^2=r_3^2\\ \cdots\\ (\vec{x}'-\vec{y}_n')^2=r_n^2 \end{cases} $$

    下面 n−1n-1 个式子同时减去 (1)(1)，得到

    $$\begin{cases} -2\vec{y}'_2\cdot\vec{x}+\vec{y}_2'^2=r_2^2-r_1^2\\ -2\vec{y}'_3\cdot\vec{x}+\vec{y}_3'^2=r_3^2-r_1^2\\ \cdots\\ -2\vec{y}'_n\cdot\vec{x}+\vec{y}_n^2=r_n^2-r_1^2 \end{cases} $$

    这等价于线性方程组

    Ax⃗=a⃗A\vec{x}=\vec{a} $$A=\begin{bmatrix} (\vec{y}_2')^T\\ \hline(\vec{y}_3')^{T^{^{^{}}}}\\ \hline\vdots \\ \hline(\vec{y}_n')^{T^{^{^{}}}} \end{bmatrix},\vec{a}=-\dfrac{1}{2}\begin{bmatrix} r_2^2-r_1^2-\vec{y}_2^2\\ r_3^2-r_1^2-\vec{y}_3^2\\ \vdots\\ r_n^2-r_1^2-\vec{y}_n^2 \end{bmatrix}$$

    高斯消元求解该线性方程组，若其有唯一解，则解就是答案。

    如果解不是唯一的怎么办？这时“形”便派上用场。

    让我们转换一下题意：给定 dd 维空间中 nn 个超球，

    球心为 y⃗1,y⃗2,⋯ ,y⃗n\vec{y}_1,\vec{y}_2,\cdots,\vec{y}_n，半径为 r1,r2,⋯ ,rnr_1,r_2,\cdots,r_n，求它们的交点。

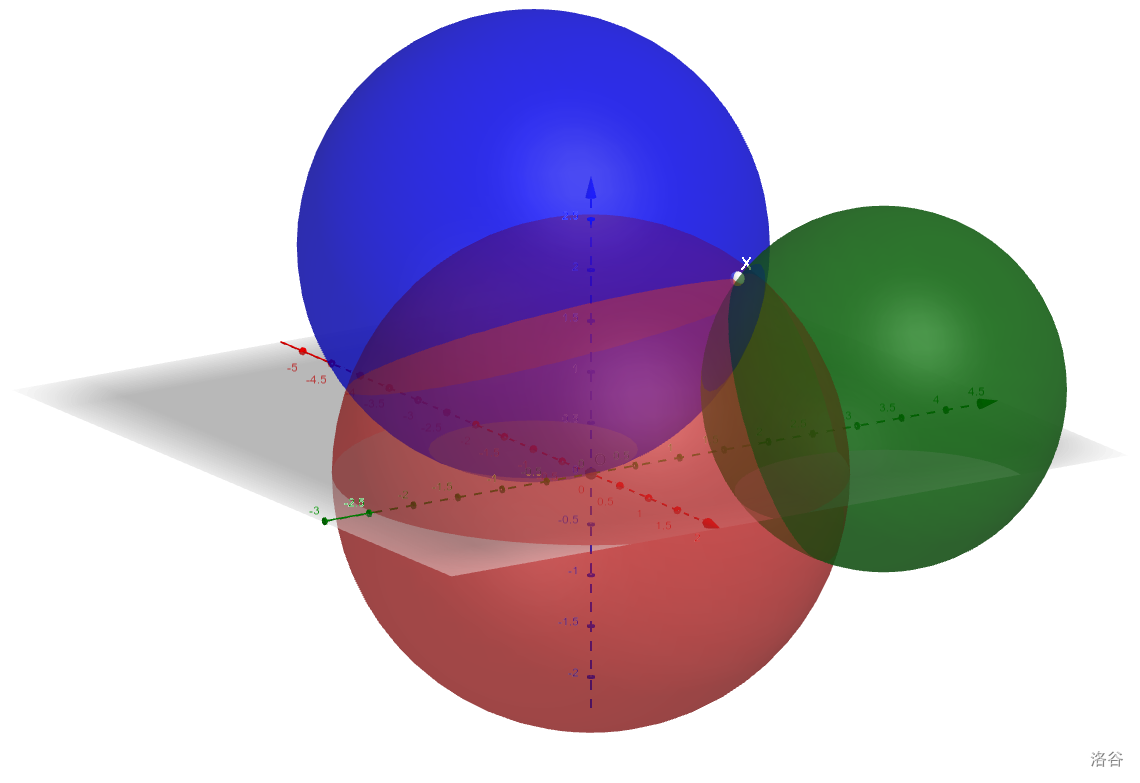
    先把这个问题搁置一边，来看看这个高中文化课常用的 trick：

    给定二维空间两个圆的方程：

    $$\begin{cases} (x-a_1)^2+(y-b_1)^2=r_1^2&(1)'\\ (x-a_2)^2+(y-b_2)^2=r_2^2&(2)' \end{cases} $$

    它们的交线如图所示：

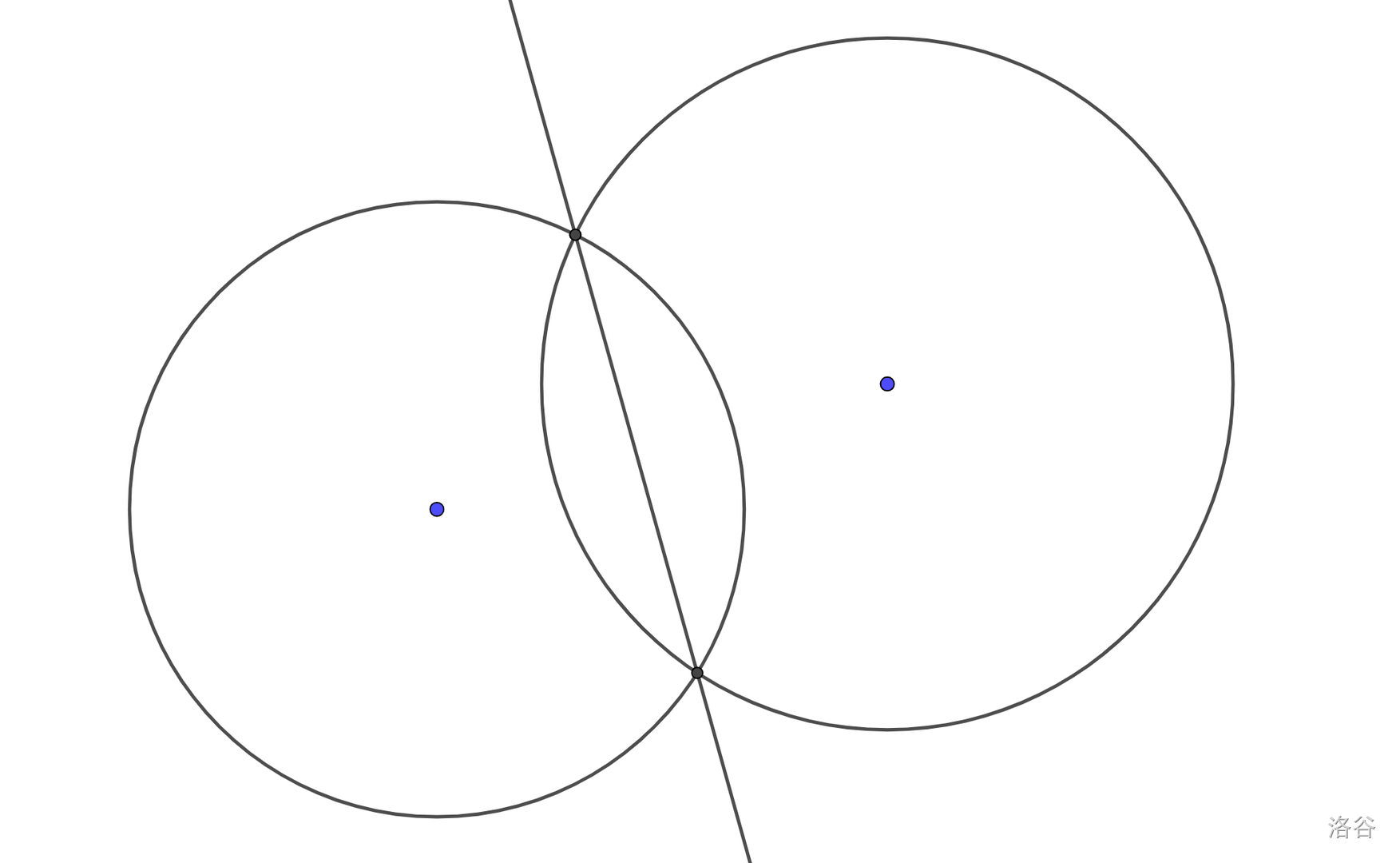
    现在我们要求交线的方程，一般人的想法是将 (1)′,(2)′(1)',(2)' 联立，求得交点后再求交线。

    但最快的方法是将 (1)′,(2)′(1)',(2)' 相减，直接求得交线的方程

    $$(x-a_1)^2-(x-a_2)^2+(y-b_1)^2-(y-b_2)^2=r_1^2-r_2^2 $$

    接下来我们简短证明下这么做的正确性：

    • (1)′,(2)′(1)',(2)' 中 x2,y2x^2,y^2 系数均为 11，因此 (1)′−(2)′(1)'-(2)' 一定是个二元一次不定方程，
      也就一定是一条直线。
    • (2)′+[(1)′−(2)′]=(1)′(2)'+[(1)'-(2)']=(1)'，因此圆 22 与该直线的交点一定在圆 11 上。
      同理，圆 11 与该直线的交点一定在圆 22 上。
      因此该直线与两个圆中一个的交点等价于两个圆的交点。
      综上，(1)′−(2)′(1)'-(2)' 就是两个圆的交线方程。

    显然这个结论及其证明可以推广到高维空间，若已知三维空间两个球的方程：

    $$\begin{cases} (x-a_1)^2+(y-b_1)^2+(z-c_1)^2=r_1^2&(1)''\\ (x-a_2)^2+(y-b_2)^2+(z-c_2)^2=r_2^2&(2)''\\ \end{cases} $$

    它们的交面如图所示：

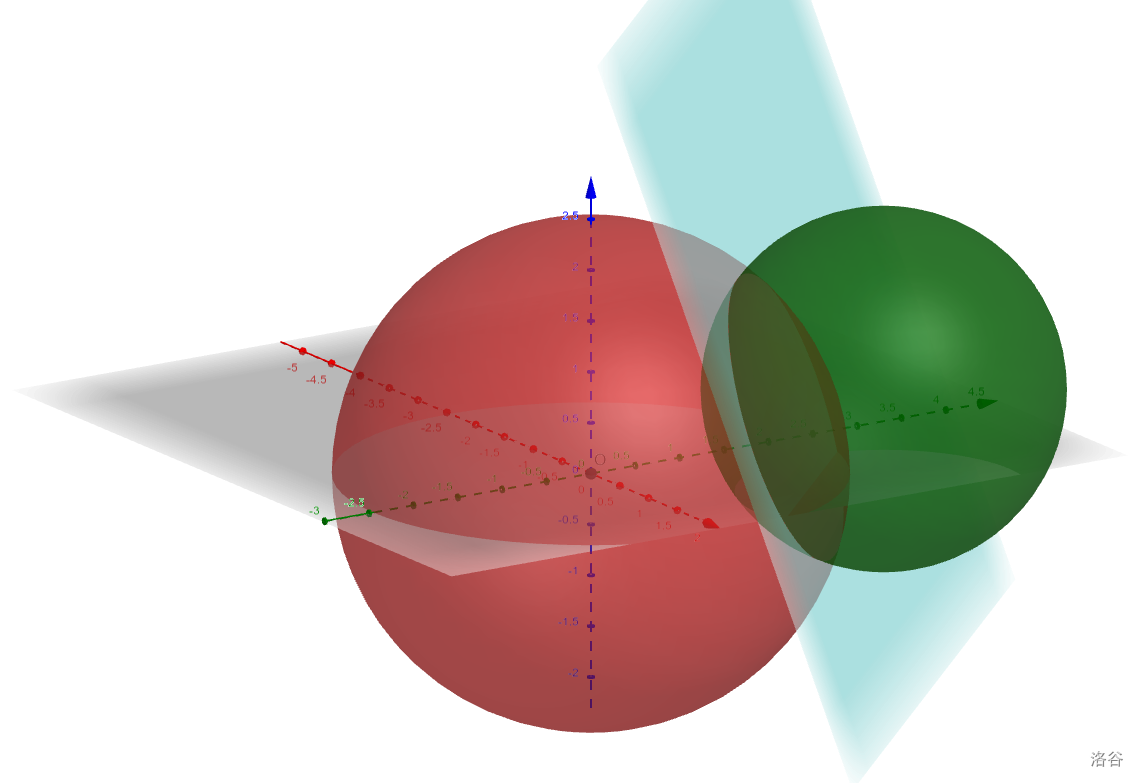
    把 (1)′′(1)'' 和 (2)′′(2)'' 相减，可直接得到交面的方程

    $$(x-a_1)^2-(x-a_2)^2+(y-b_1)^2-(y-b_2)^2+(z-c_1)^2+(z-c_2)^2=r_1^2-r_2^2 $$

    且交面与其中一个球的交点等价于两球的交点。

    同理，若已知 dd 维空间的两个超球：

    $$\begin{cases} (\vec{x}-\vec{y}_1)^2=r_1^2\\ (\vec{x}-\vec{y}_2)^2=r_2^2 \end{cases} $$

    将两个超球的方程相减，可得到 d−1d-1 维超交面的方程

    $$(\vec{x}-\vec{y}_1)^2-(\vec{x}-\vec{y}_2)^2=r_1^2-r_2^2 $$

    且超交面与其中一个超球的交点等价于两个超球的交点。

    此时我们已经能解释之前的高斯消元在做什么了：

    • 将所有方程减去 (1)(1) 等价于求超球 11 与其他所有超球的超交面方程。
    • 高斯消元等价于求这些超交面的交。
    • 这些超交面的交与超球 11 的交点都是合法的解，即所有超球的交点。

    分析完这些后，解不唯一的情况变成了一个这样的问题：

    设高斯消元后自由元的个数为 kk，
    则我们需要求解一个 dd 维超球和一个 kk 维 “平面” （准确的说是线性流形）的交点。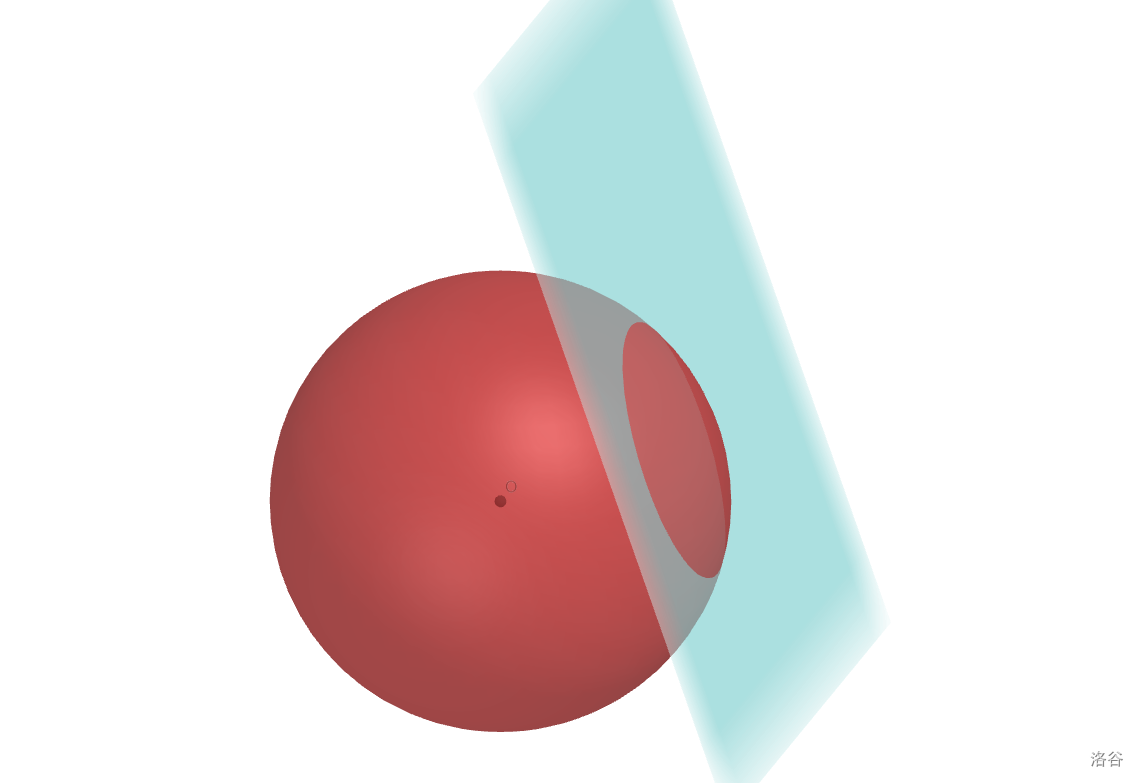

    同样考虑二维空间的情况：求解一个圆和一条直线的交点。

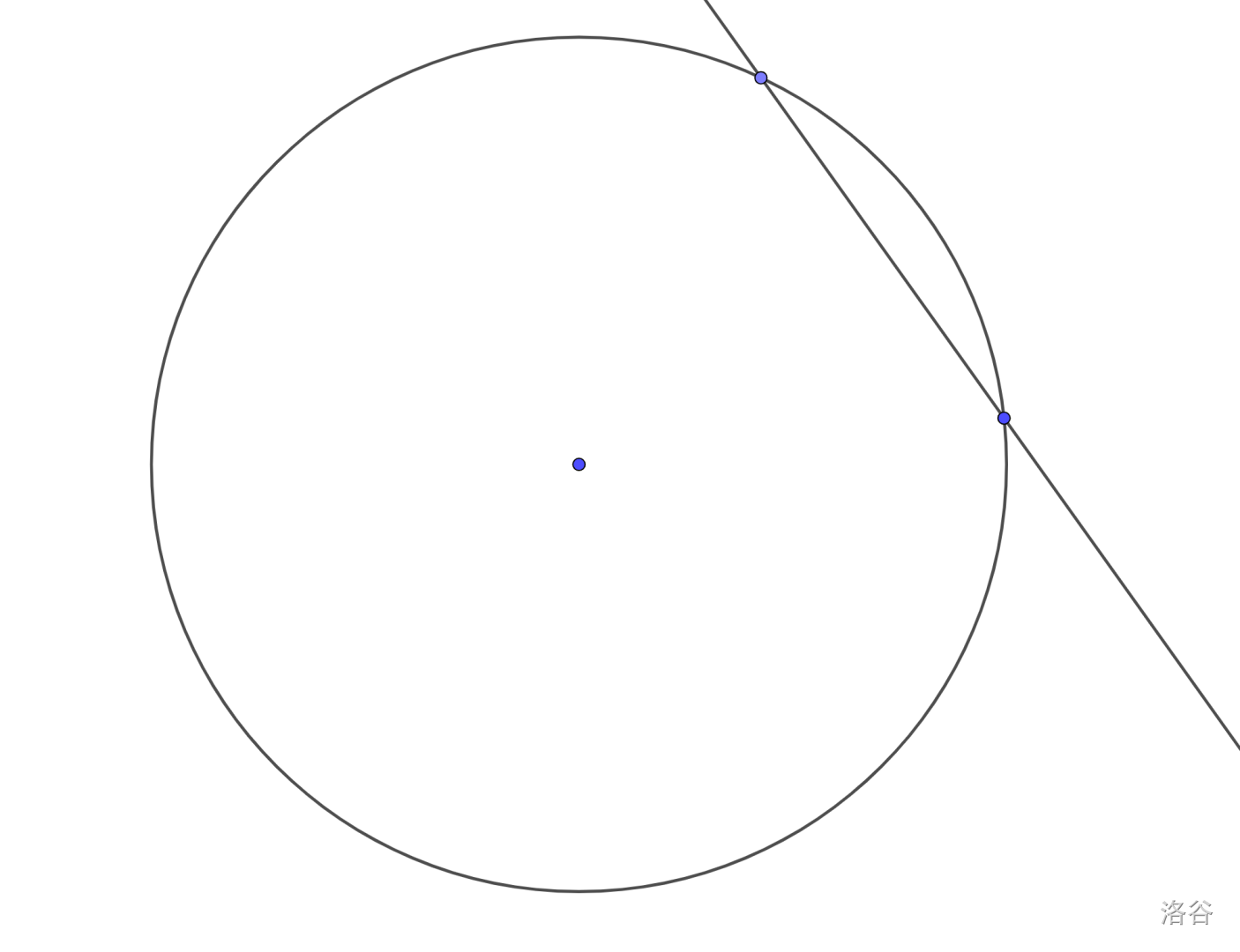
    一个显然的做法是过圆心向直线作垂线，然后勾股定理算出垂足到交点的距离：

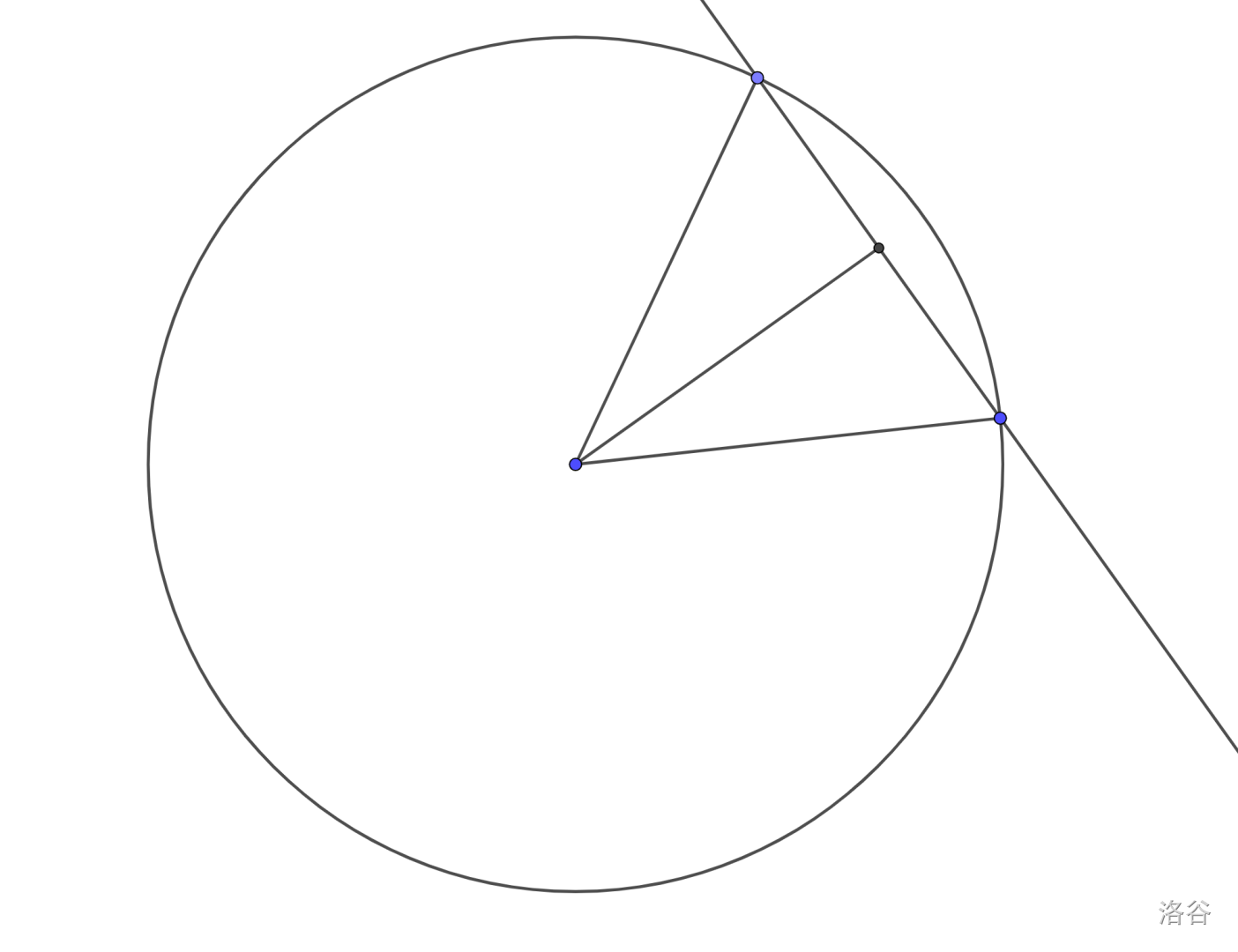
    拓展到三维空间时，情况是类似的：

    • 对于三维空间一条直线和球相交，跟刚才的情况是一样的。
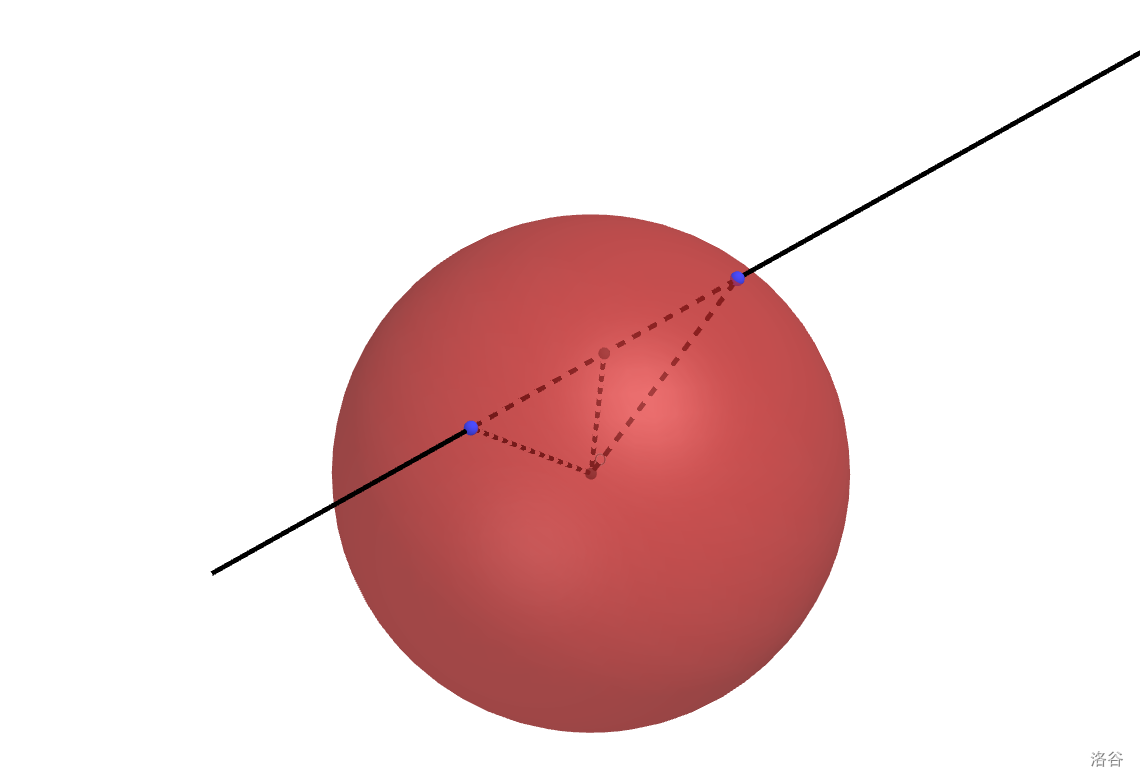
    • 对于三维空间一个平面和球相交，可以确定截面一定是个圆。 同样作垂线得到圆心后勾股定理求解。

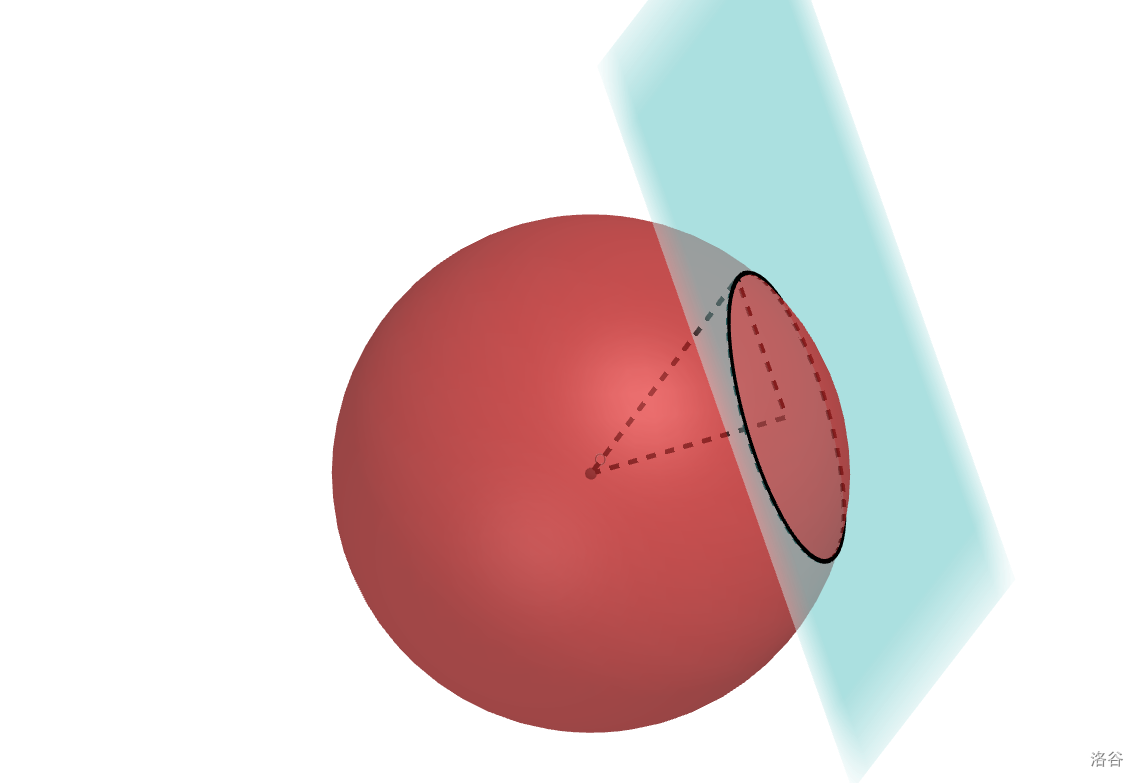
    想一想怎么归纳到高维空间，提示一下：一维空间的超球是两个点。

    \qquad

    \qquad

    答案揭晓：dd 维空间一个超球与一个 k(k≤d)k(k\le d) 维线性流形相交，截面一定是个 kk 维超球。
    过原超球球心向线性流形作垂线即可得到截面的球心，再勾股定理即可得到球心的半径。

    我们由此得到求解原问题的一个大致的思路：

    • 过超球心向线性流形作垂线，求出垂足的坐标 p⃗\vec{p}。
    • 勾股定理算出截面的半径 r′r'。
    • 在线性流形上随便找一个长度为 r′r' 的向量 q⃗\vec{q}，p⃗+q⃗\vec{p}+\vec{q} 就是一个合法的解。

    回到之前的线性方程组。高斯消元后，其一定会变为如下形式：

    $$\left[ \begin{array}{ccccc|} 1&&&&&v_{1,1}&v_{2,1}&\cdots&v_{k,1}\\ &1&&&&v_{1,2}&v_{2,2}&\cdots&v_{k,2}\\ &&\ddots&&&\vdots&\vdots&\vdots&\vdots\\ &&&1&&v_{1,d-k-1}&v_{2,d-k-1}&\cdots&v_{k,d-k-1}\\ &&&&1&v_{1,d-k}&v_{2,d-k}&\cdots&v_{k,d-k}\\ \hline 0&0&0&0&0&0&0&0&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \end{array}\right] \begin{bmatrix} x_1\\x_2\\\vdots\\x_{d-k}\\\hline x_{d-k+1}\\ x_{d-k+2}\\ \vdots \\x_d \end{bmatrix}=\begin{bmatrix} a_1'\\ a_2'\\ \vdots\\ a_{d-k}'\\\hline 0\\0\\ \vdots \\0 \end{bmatrix} $$

    简记为如下形式：

    $$\left[\begin{array}{c|c|c|c|c} I&\vec{v}_1&\vec{v}_2&\cdots&\vec{v}_k\\ \hline O&\vec{0}&\vec{0}&\vec{0}&\vec{0} \end{array}\right] \begin{bmatrix}\vec{x}_0\\ \hline\vec{x}_1\end{bmatrix} =\begin{bmatrix}\vec{a}'\\ \hline\vec{0}\end{bmatrix} $$

    我们需要确定线性方程组的解集，从而确定整个线性流形。

    • 若 x⃗1=0⃗\vec{x}_1=\vec{0}，显然 x⃗0=a⃗′\vec{x}_0=\vec{a}'。
      因此 $\begin{bmatrix}\vec{a}'\\ \hline\vec{0}\end{bmatrix}$ 是该线性方程组的一组特解。
    • 若 xd−k+1=λ,xd−k+2=xd−k+3=⋯=xd=0x_{d-k+1}=\lambda,x_{d-k+2}=x_{d-k+3}=\cdots=x_d=0，
      则 $\vec{x}_0+\lambda\vec{v}_1=\vec{a}',\vec{x}_0=\vec{a}-\lambda\vec{v}_1$。
      因此 xd−k+1x_{d-k+1} 每增加 λ\lambda，x⃗0\vec{x}_0 就要减去 λv⃗1\lambda\vec{v}_1。

    综上，设

    $$\vec{u}_1=\begin{bmatrix}-\vec{v}_1\\\hline 1\\0\\0\\0\\ \vdots\end{bmatrix} ,\vec{u}_2=\begin{bmatrix}-\vec{v}_2\\\hline 0\\1\\0\\0\\ \vdots\end{bmatrix}, \vec{u}_3=\begin{bmatrix}-\vec{v}_3\\\hline 0\\0\\1\\0\\ \vdots\end{bmatrix},\cdots $$$$\vec{b}=\begin{bmatrix} \vec{a}'\\ \hline \vec{0} \end{bmatrix},V=\{[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]\vec{x}_1|\vec{x}_1\in\mathbb{R}_k\} $$

    则线性方程组的解集为

    X={b⃗+Δ⃗∣Δ⃗∈V}X=\{\vec{b}+\vec{\Delta}|\vec{\Delta}\in V\}

    即线性空间 VV 内的所有向量加上特解 b⃗\vec{b}，与线性流形的定义一致。

    接下来考虑作垂线，由于球心为 0⃗\vec{0}，VV 的基底为 u⃗1,u⃗2,⋯ ,u⃗k\vec{u}_1,\vec{u}_2,\cdots,\vec{u}_k，
    我们的目标是找出 p⃗∈X\vec{p}\in X，使得 p⃗\vec{p} 与 VV 中所有的基向量垂直，即

    $$\vec{u}_1\cdot \vec{p}=\vec{u}_2\cdot\vec{p}=\cdots=\vec{u}_k\cdot \vec{p}=0 \qquad{(2)}$$

    把 p⃗\vec{p} 拆开：

    $$\vec{p}=\vec{b}+[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]\vec{x}_1\qquad{(3)} $$

    然后将 (2)(2) 表示成矩阵形式：

    $$\begin{bmatrix} \vec{u}_1^T\\ \hline\vec{u}_2^{T^{^{^{}}}}\\ \hline\cdots\\ \hline\vec{u}_k^{T^{^{^{}}}} \end{bmatrix}(\vec{b}+[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]\vec{x}_1)=\vec{0} $$

    注意到 $\begin{bmatrix}\vec{u}_1^T\\\hline\vec{u}_2^{T^{^{^{}}}}\\\hline\cdots\\\hline\vec{u}_k^{T^{^{^{}}}} \end{bmatrix}[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]$ 为 kk 阶方阵 ，因此高斯消元解线性方程组

    $$\begin{bmatrix}\vec{u}_1^T\\\hline\vec{u}_2^{T^{^{^{}}}}\\\hline\cdots\\\hline\vec{u}_k^{T^{^{^{}}}} \end{bmatrix}[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]\vec{x}_1=-\begin{bmatrix}\vec{u}_1^T\\\hline\vec{u}_2^{T^{^{^{}}}}\\\hline\cdots\\\hline\vec{u}_k^{T^{^{^{}}}} \end{bmatrix}\vec{b} $$

    即可得到 x⃗1\vec{x}_1，代入 (3)(3) 即可求出 p⃗\vec{p}。

    因为过线性流形（直线/平面）上一点有且只有一条直线与该流形（直线/平面）垂直，

    这个线性方程组一定有唯一解，也就一定能解出 p⃗\vec{p}。

    解出 p⃗\vec{p} 后，勾股定理得到

    r′=r2−p⃗2r'=\sqrt{r^2-\vec{p}^2}

    然后 p⃗+r′u⃗12u⃗1\vec{p}+\dfrac{r'}{\sqrt{\vec{u}_1^2}}\vec{u}_1 就是一组合法的解了。

    最后不要忘记，我们一开始将原点平移到了 y⃗1\vec{y}_1，要平移回去才行哦！

    Code

    /*
this code is made by warzone
2022.3.11 15:30
*/
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
typedef double db;
struct READ{//快读
	char c,w;
	inline READ(){c=getchar();}
	template<typename type>
	inline READ& operator >>(type& num){
		for(w=1;'0'>c||c>'9';c=getchar())
			w=c=='-'? -1:1;
		for(num=0;'0'<=c&&c<='9';c=getchar())
			num=num*10+(c-'0');
		if(c=='.') for(db i=1;c=getchar(),'0'<=c&&c<='9';)
			i*=0.1L,num+=i*(c-'0');
		return num*=w,*this;
	}
}cin;
int d,n;
int pos[512],pos_[512];
db y[512],r;
db A[512][512],a[512];
db B[512][512],b[512];
int top,top_;
template<typename type1,typename type2,typename type3>
inline void gauss(type1 &A,type2 &a,type3 &pos,//高斯消元
	int &top,const int d,const int n){
	top=d;
	for(int id=0;id<top&&id<n;++id){
		while(A[id][id]==0){
			for(int i=id+1;i<n;++i) if(A[i][id]){
				for(int j=id;j<d;++j)
					std::swap(A[id][j],A[i][j]);
				std::swap(a[id],a[i]);break;
			}
			if(A[id][id]==0){//把消元失败的维度放到最后面
				if(id>=--top) return;
				std::swap(pos[top],pos[id]);
				for(int i=0;i<n;++i)
					std::swap(A[i][id],A[i][top]);
			}
		}
		if(A[id][id]!=1){
			db get=A[id][id];
			for(int i=id+1;i<d;++i) A[id][i]/=get;
			A[id][id]=1,a[id]/=get;
		}
		for(int i=0;i<n;++i) if(i!=id&&A[i][id]){
			db get=A[i][id];
			for(int j=id+1;j<d;++j) A[i][j]-=A[id][j]*get;
			A[i][id]=0,a[i]-=a[id]*get;
		}
	}
}
inline void print(){//平移回来并输出答案
	for(int i=0;i<d;++i) y[pos[i]]+=a[i];
	for(int i=0;i<d;++i) printf("%0.6lf ",y[i]);
}
int main(){
	cin>>d>>n;
	for(int i=0;i<d;++i) cin>>y[i],pos[i]=i;//输入 (1) 式
	cin>>r,--n;
	for(int id=0;id<n;++id){
		for(int i=0;i<d;++i){//减去 (1) 式
			cin>>A[id][i],A[id][i]-=y[i];
			a[id]+=A[id][i]*A[id][i];
		}
		db get;
		cin>>get,a[id]=(a[id]+r*r-get*get)/2;
	}
	gauss(A,a,pos,top,d,n),top=std::min(top,n);//第一次高斯消元
	if(top==d) return print(),0;//唯一解
	for(int i=top;i<d;++i) A[i][i]=-1;
	const int k=d-top;
	for(int id=0;id<k;++id){//计算 \vec{p} 的线性方程组
		pos_[id]=id;
		for(int i=0;i<k;++i)
			for(int j=0;j<d;++j)
				B[id][i]+=A[j][id+top]*A[j][i+top];
		for(int j=0;j<d;++j)
			b[id]-=A[j][id+top]*a[j];
	}
	gauss(B,b,pos_,top_,k,k);//第二次高斯消元
	for(int id=0;id<k;++id)//将 \vec{x}_1 代回 \vec{p} 
		for(int i=0;i<d;++i)
			a[i]+=b[id]*A[i][id+top];
	db r_=r*r,r__=0;
	for(int i=0;i<d;++i){//勾股定理计算 r'
		r__+=A[i][top]*A[i][top];
		r_-=a[i]*a[i];
	}
	r_=sqrtl(r_/r__);
	for(int i=0;i<d;++i) a[i]+=A[i][top]*r_;
	return print(),0;
}
    • 1

    [ICPC 2020 WF] What’s Our Vector, Victor?

    信息

    ID
    7487
    时间
    6000ms
    内存
    512MiB
    难度
    7
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 34ms