自动搬运

查看原文

来自洛谷，原作者为

	Diaоsi Enemy of God

搬运于2025-08-24 22:36:16，当前版本为作者最后更新于2024-05-25 13:02:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

[ICPC2020 WF] Ley Lines

抢一下第一篇题解，本题解采用弧度制，其中 $\sin^{-1},\,\tan^{-1}$ 为反三角函数。

首先有一个引理，就是一定存在一个最优解使得有一个点在线的边界上。证明很简单，如果不在边界上的话，我们可以平移两条线，直到其中一条碰到某个点为止。不难发现在这个过程中答案是不会变的。

枚举那个在边界上的点。然后以这个点为原点，模拟粗线转绕原点转一圈的过程，求出在这个过程中每个点分别在哪个角度区间会被覆盖。

遍历其余的点，设当前点的极角为 $\alpha$，与原点（当前）距离为 $d$，粗线宽为 $r$。

若 $d<r$，则该点被覆盖的幅角为 $[\alpha,\alpha+\pi]$。

若 $d\geq r$，则该点被覆盖的幅角为 $[\alpha,\alpha+\beta]$ 和 $[\alpha-\beta+\pi,\alpha+\pi]$。

可以画图理解，下图以区间 $[\alpha,\alpha+\beta]$ 为例：

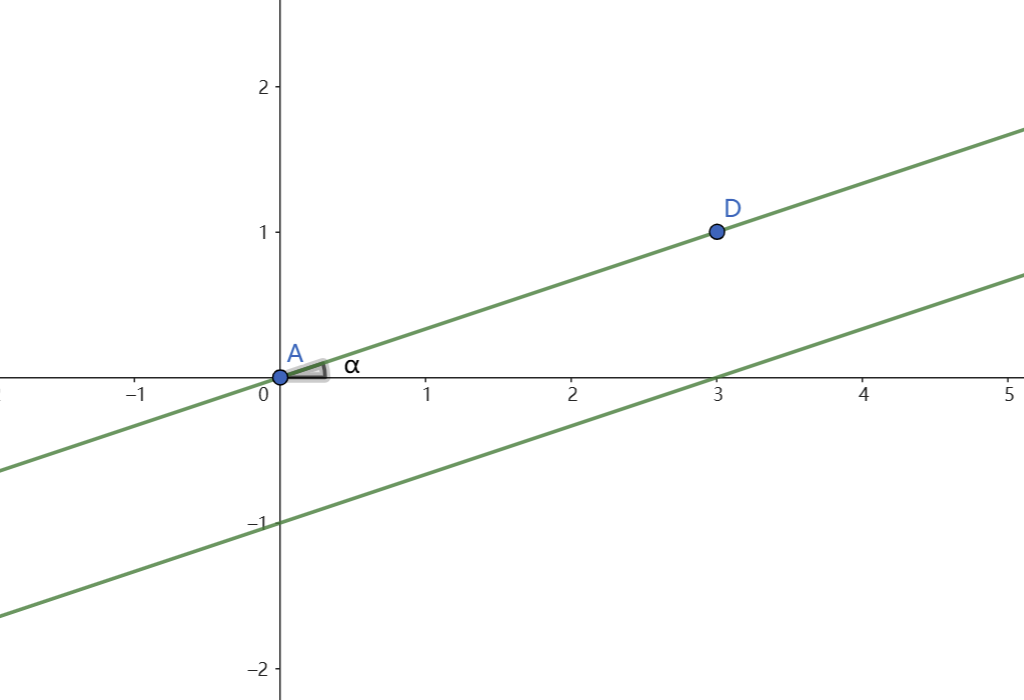
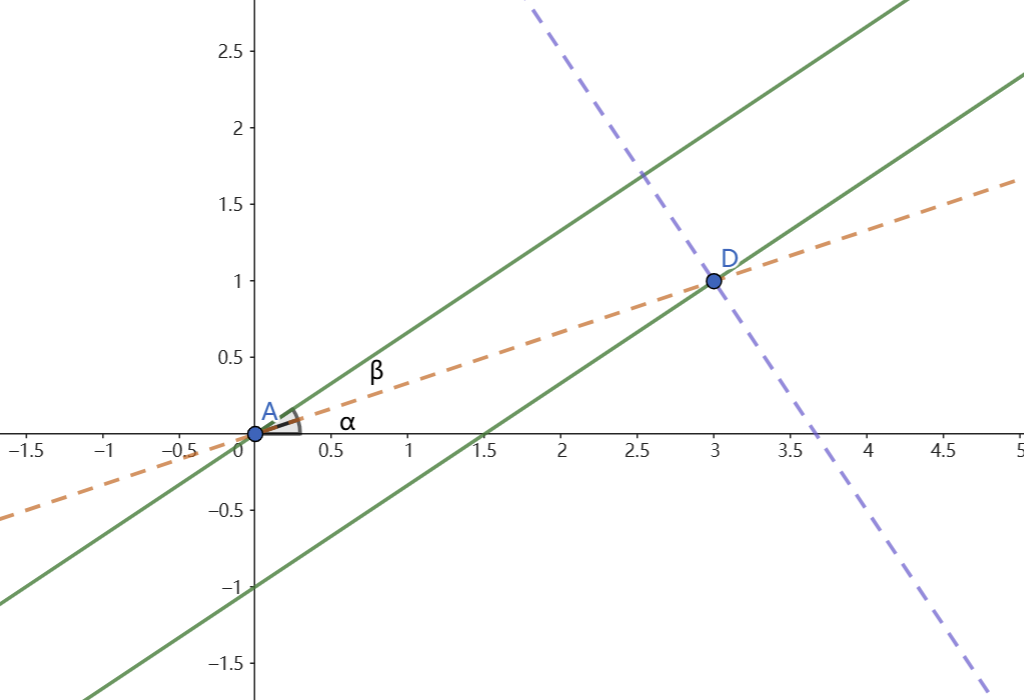
把所有区间处理出来后，按照极角升序做一遍扫描线即可，时间复杂度 $\mathcal{O}(n^2\log n)$。

#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pb push_back
typedef long long ll;
typedef long double ld;
using namespace std;
const int N=3010,M=30010,INF=0x3f3f3f3f;
const ld eps=1e-6,pi=acos(-1),inf=1e9;
int n,m,ans,res;
vector<pair<ld,int> > v;
struct node{
	ll x,y;
	node(ll xx=0,ll yy=0){x=xx,y=yy;}
	void in(){scanf("%lld%lld",&x,&y);}
	void out(){printf("%lld %lld\n",x,y);}
}p[N];

node operator +(node a,node b){return node(a.x+b.x,a.y+b.y);}
node operator -(node a,node b){return node(a.x-b.x,a.y-b.y);}
ll operator *(node a,node b){return a.x*b.x+a.y*b.y;}
ll operator ^(node a,node b){return a.x*b.y-a.y*b.x;}

node operator *(ll x,node b){return node(x*b.x,x*b.y);}

ld sqr(ld x){return x*x;}
ld dis(node a,node b){return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));}

ld get(ld x){return x<0?2*pi+x:x;}
ld taninv(ld y,ld x){return get(atan2(y,x));}

void add(ld l,ld r){
	v.pb(mp(l,1)),v.pb(mp(r,-1));
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)p[i].in();
	for(int i=1;i<=n;i++){
		v.clear();res=1;
		for(int j=1;j<=n;j++){
			if(i==j)continue;
			node b=p[j]-p[i];
			ld t=taninv((ld)b.y,(ld)b.x),r=dis(p[i],p[j]),s=asin((ld)m/r);
			if(r<(ld)m)add(t,t+pi);
			else add(t,t+s),add(t-s+pi,t+pi);
		}
		sort(v.begin(),v.end());
		for(pair<ld,int> t:v)
			res+=t.se,ans=max(ans,res);
	}
	printf("%d\n",ans);
	return 0;
}