自动搬运

查看原文

来自洛谷，原作者为

	Cocoly1990 成事不说 遂事不谏 既往不咎

搬运于2025-08-24 22:35:52，当前版本为作者最后更新于2022-02-03 21:49:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

D

part1 问题等价于给定一颗完全二叉树，求其包含根的子树个数。 首先，先考虑满二叉树。 我们可以发现，答案只和树的深度(dep)有关，可以想到用 $dp_i$ 表示深度为 $i$ 的满二叉树的答案。

显然 $dp_1 = 1$ 。我们考虑用 $dp_{i - 1}$ 来计算 $dp_i$。

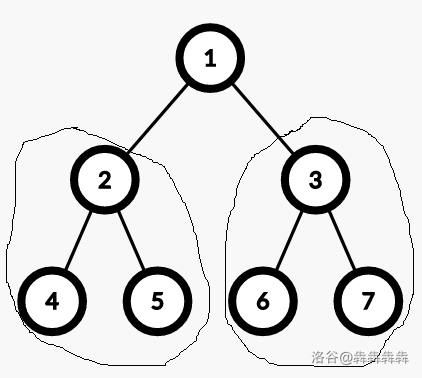
以 $dp_3$ 为例，我们可以发现，1 号节点为根节点，必须选。 对于每一种左子树和右子树的方案，我们只需要直接加上根节点，就可以对应一种新树的方案；而对于每一种新树的方案，去掉根节点就可以对应到一种左右子树的方案。由乘法原理可以得知其答案为左子树与右子树的选法乘积。 我们可以直接利用已经算出来的 $dp_2$ ，表示深度为 2 的包含根的子树个数，但是 $dp_2$ 包含的方案中，不包括不选子树的根节点的情况。但是在新树中，我们没有这个要求，我们还可以左子树一个都不选，所以 $dp_i = (dp_{i - 1} + 1) ^ 2$。 期望得分：20。

part2 类似的，我们也可以通过分别递归计算左右子树答案，再相乘的做法来对一颗不规则的树来计数。

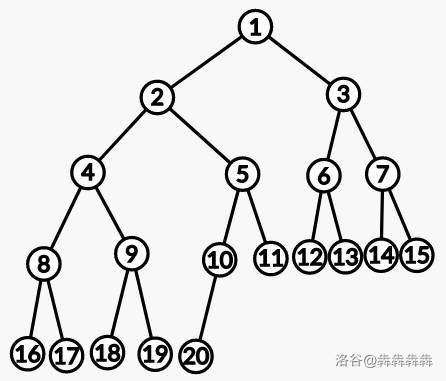
以一颗深度为 5 ，底层节点数为 5 的树为例。我们可以拆成以 2 和 3 为根节点的子树分别递归地去求，求完后相乘。 我们按从上到下，从左到右给树标号，若 $d_i$ 表示以 $i$ 为根的答案，则 $d_i = (d_{2i} + 1)(d_{2i + 1} + 1)$ 。直接 dfs 即可，答案为 $d_1$。 由于我们需要对于每一个节点递归一次，复杂度为 $\mathcal{O}(T\times 2^{dep})$。 结合 part1，期望得分：50。

part3 我们可以发现，在我们的 dfs 中，有许多满二叉树，所以我们根本不需要对每个节点 dfs 一次。

比如以 3，4，11 为根节点的子树分别就是深度为 3, 2, 1 的满二叉树。 更形式化的，我们可以发现，对于每一个节点，其左右子树中必有一颗为满二叉树。 由完全二叉树的性质，若右子树不为满二叉树，则其左子树必为满二叉树，而若左子树不为满二叉树，则其底层节点根本没有覆盖到右子树，右子树为满二叉树。 所以，我们可以用 part1 的做法，预处理出所有满二叉树的答案。每次 dfs 的，直接调用即可。而我们只需要 dfs 一条链。（图中 1-2-5-10-20） 所以，我们的问题变为对于每个节点，确定其哪颗子树为满二叉树，并且求出子树高度。即我们需要求出从根节点到最后一个叶节点的路径，每次 dfs 路径上的下一个节点，直接调用求出另外一个节点的答案。 观察到本题给出底层节点个数的方式非常特殊，用二进制给出。暂时忽略满二叉树的情况，去掉第一个0，比如 5 为 0101。我们从根节点开始，对于这个二进制字串，从左到右，如果遇到 0 就走左子树，遇到 1 就走右子树，我们可以发现对于任意一棵树，我们都可以走到当前最后一个节点的下一个节点。

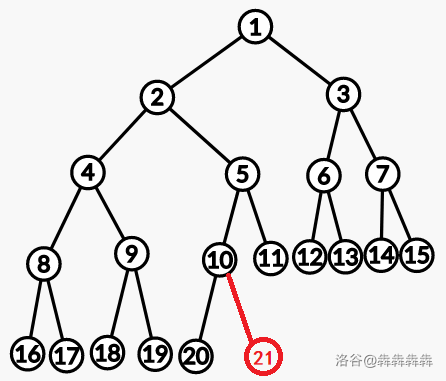
仔细研究一下，我们可以发现 5 的 00101，第一位的 0 表示其节点数小于 16 ，即位于根为 1 的子树上，而第二个 1 表示其节点数小于 8，位于 1 的左子树上，第三个 1 表示其节点数大于等于 4 ，位于 2 的右子树上。 由此，我们再考虑满二叉树，图中满二叉树底层节点为 16，表示为 10000，第一位的 1 表示其节点数大于等于 16，即其最后一个节点的下一个节点根本就不在根为 1 的子树上。 设其底层节点个数为 $s$， $s$ 的二进制表示可以直接求出其最后一个节点的下一个节点的路径，那么 $s - 1$ 的二进制表示的就是我们需要求的路径了。 下面是求出子树高度，设当前节点深度为 k，那么若左子树为满二叉树，那么从根节点到当前叶节点的距离为 dep，即高度为 $dep - k$。若是右子树为满二叉树，由于缺少了底层节点，其距离为 $dep - 1$，即树高为 $dep - k - 1$。 由于我们每次只会 dfs 一条链，所以复杂度为 $\mathcal{O}(T \times dep)$。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 1e6 + 5;
const int MOD = 998244353;
int dep, a[MAXN], dp[MAXN];
string s;
int dfs(int k) {
	if (k == dep)
		return 1; //到最后一层
	if (a[k] == 0) 
		return (dfs(k + 1) + 1) * (dp[dep - k - 1] + 1) % MOD; //右子树为满二叉树，dfs左子树
	else return (dp[dep - k] + 1) * (dfs(k + 1) + 1) % MOD; //左子树为满二叉树，dfs右子树
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	dp[1] = 1;
	for (int i = 1; i < MAXN; ++i)
		dp[i] = (dp[i - 1] + 1) * (dp[i - 1] + 1) % MOD; //预处理
	int T;
	cin >> T;
	while (T--) {
		cin >> dep >> s;
		int pos = 0;
		for (int i = 1; i < s.length(); ++i) {
			a[i] = s[i] - '0';
			if (a[i] == 1)
				pos = i;
		}
		a[pos] = 0; 
		for (int i = pos + 1; i < dep; ++i)
			a[i] = 1;//s-1 的二进制表达
		cout << dfs(1) << endl;
	}
	return 0;
}

当然还有另一种优化方法，由 Part 2 我们得到转移方程 $f_i = (f_{2i} + 1)(f_{2i + 1} + 1)$.（嗯上下两个题解不是同一个人写的）。

显然状态不是很好优化，那么思考如何优化转移。可以发现，每个 $f_x$ 是相互独立的，也就是说，我们可以把特殊的 $f_x$ 预处理出来。 考虑到满二叉树总共只有 $\log n$ 种，不妨把他们的染色方案与处理出来，预处理他们的时间复杂度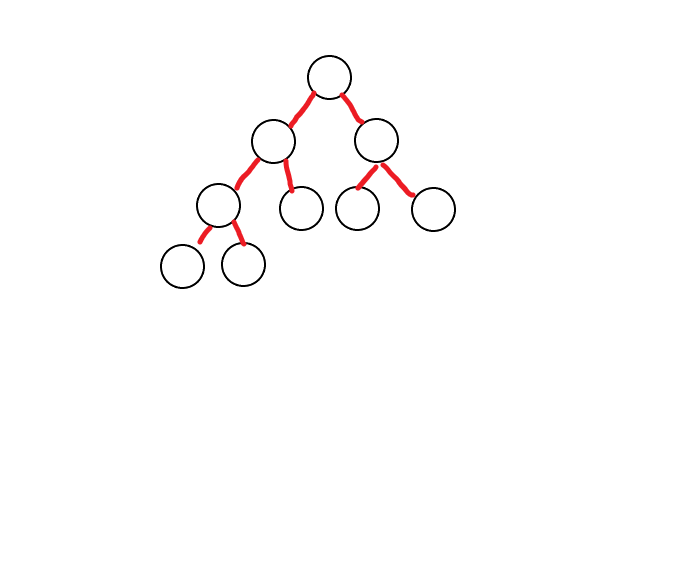$\mathcal{O}\left(dep\right)$ 比如这颗树，我们把能预处理的满二叉树给他处理掉。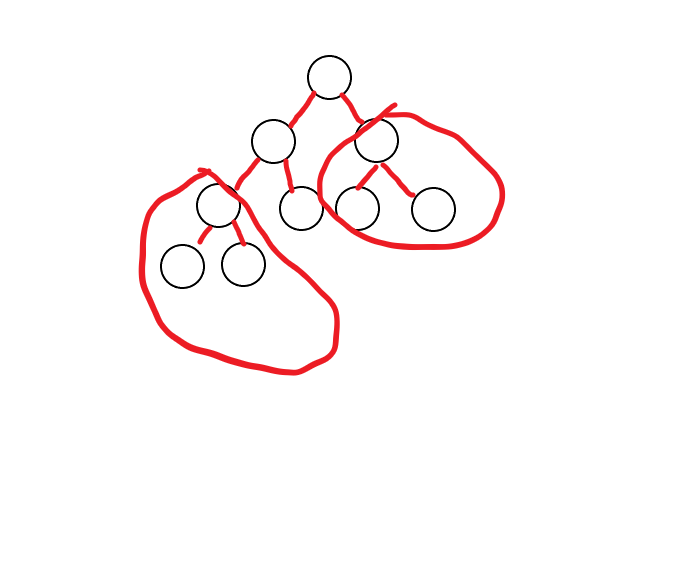

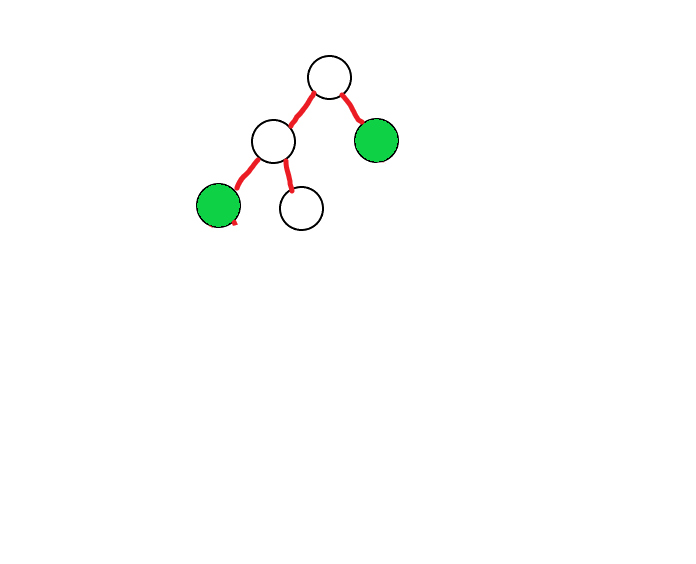
绿色表示处理过的，然后会发现每层只有两个节点需要向上传递。所以复杂度是对数级别的。

我们可以通过 $s$ 处理出 $s_0$ 表示次底层的叶子节点。（二进制高精度）

具体的说，对 $s$ 从左向右处理 1 ，处理到 $\texttt{dep}$ 数组里，表示当前每层预处理的结果。 $s_0$ 从右向左处理 1 ，同样储存到数组里，如果碰到已经储存过的位置，那么从那个点开始向上递推。

#include<bits/stdc++.h>
#define int long long
#define elif else if
#define ALL(x) x.begin(),x.end()
#define lowbit(x) (x&(-x))
using namespace std;
void fileio(const string &s)
{
	freopen((s+".in").c_str(),"r",stdin);
	freopen((s+".out").c_str(),"w",stdout);
}
const int INF=4e18;
inline int read()
{
	int x=0;
	bool flag=1;
	char c=getchar();
	while(c<'0'||c>'9')
	{
		if(c=='-')
			flag=0;
		c=getchar();
	}
	while(c>='0'&&c<='9')
	{
		x=(x<<1)+(x<<3)+c-'0';
		c=getchar();
	}
	return (flag?x:~(x-1));
}
const int mod=998244353;
int t,dep,a[1000001];
vector<int> f[1000001];
char s1[1000000],s2[1000000];
void solve()
{
	dep=read();//8 00111001 00100011
	scanf("%s",s1);
	scanf("%s",s2);//假设s1是最底层叶子节点，s2是次底层叶子节点。具体的需要二进制高精度。
	reverse(s1,s1+dep);
	reverse(s2,s2+dep);
	for(int i=0;i<=dep;i++)
		f[i].clear();
	for(int i=0;i<dep;i++)
		if(s1[i]=='1')
			f[dep-i].push_back(a[i+1]);
	for(int i=0;i<dep;i++)
		if(s2[i]=='1')
			f[dep-i-1].push_back(a[i+1]);
	for(int i=dep;i;i--)
		if(f[i].size()==1)
			f[i-1].push_back(f[i][0]+1);
		elif(f[i].size()==2)
			f[i-1].push_back((f[i][0]+1)*(f[i][1]+1)%mod);
	cout<<f[0][0]-1<<'\n';
}
signed main()
{
	a[1]=1;
	for(int i=2;i<=1000000;i++)
		a[i]=(a[i-1]+1)*(a[i-1]+1)%mod;
	t=read();
	while(t--)
		solve();
	return 0;
}

隐藏图片：

【数据删除】