自动搬运

查看原文

来自洛谷，原作者为

	泥土笨笨 《算法竞赛实战笔记》作者

搬运于2025-08-24 22:35:39，当前版本为作者最后更新于2022-03-09 16:33:15，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

居然成为了这道题第一个AC的人，那必须要写一篇题解了。

前置知识：拓扑排序，并查集，强连通分量。

本题问我们球迷的行动顺序，并且给了很多有向边，那么第一反应是拓扑排序，不过图上可能有环，不一定是可以拓扑排序的，所以第一步先想办法去掉环。

如果图上有若干个广场，他们的边相互都不冲突，并且他们相互可达，形成一个强连通分量，那么这些广场上的球迷中，可以任选一个先开始行动。他们会占满整个强连通分量，然后往外面去扩展。那么我们就先输出这个广场，然后其他所有在这个强连通分量里面的其他球迷我们都可以先不管，最后统一在最后输出，因为轮到他们行动的时候，他们自己的广场已经被占领了，所以他们就可以被忽略，不影响决策。所以我们可以先 tarjan 跑一下强连通分量，每个强连通分量缩成一个点，每个强连通分量里面选一个点出来做代表，其他暂时都忽略。

就这样跑强连通分量缩点，缩点以后的图上有两种边，一种是有冲突的，一种是没有冲突的。如果 $u$ 到 $v$ 的边是有冲突的，那么 $v$ 就要在 $u$ 的前面，否则 $u$ 就要在 $v$ 的前面行动。那么我们按照行动的顺序再建一张新图，在这个图上跑拓扑排序就行了。这是我一开始的想法。

但是这个看起来简单有效的做法， WA 了！我考虑了一下，有如下两种情况是有问题的。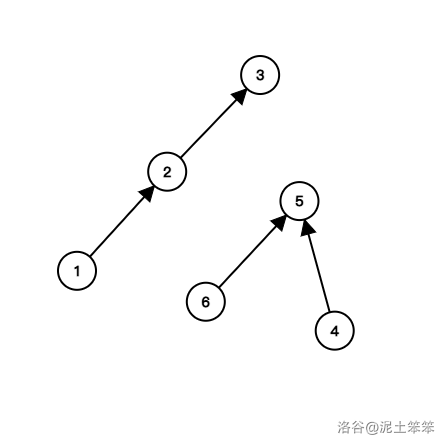

假设 $1$ 点到 $2$ 的边没有冲突， $2$ 到 $3$ 的边有冲突。那么按照刚才的做法， $1$ 到 $2$ 和 $3$ 到 $2$ 都要建边。这个时候跑拓扑排序，有可能是3 1 2，这样是合法的。但是也可能跑出来1 3 2，但是这样是错的，因为 $1$ 开始行动以后，会把 $2$ 占领，进而去占领 $3$ ，这个时候 $2$ 和 $3$ 这条边没有冲突，因为 $3$ 还没行动，这个显然是不符合题意的。

再假设 $6$ 到 $5$ 没冲突， $4$ 到 $5$ 也没冲突。这个时候按照上述算法是合法的，但是实际上也是不合法的，因为不管是 $4$ 还是 $6$ 先行动，都会占领 $5$ ，所以不可能出现 $4$ 和 $6$ 都与 $5$ 没有冲突的情况。

针对上述情况，我们需要把算法做个修正。

首先，根据刚才说的错误情况 $1$ ，拓扑排序的时候，真正的顺序是由有冲突的边决定的，而不是两种边都能决定顺序。先不考虑有冲突的边，只考虑没有冲突的边，在建图的时候，不考虑边的方向，用并查集维护一下每个连通块。当强连通分量跑完以后，新的缩点图上，每个连通块里面，只能有一个入度为 $0$ 的点。如果任何一个连通块里面有两个或者两个以上入度为 $0$ 的点，就是刚才说的错误情况 $2$ ，可以直接输出 $-1$ .如何去统计呢？可以遍历每个入度为 $0$ 的点，在并查集上找到这个点的根，在根上做个标记。如果下次发现某个入度为 $0$ 的点的根已经被标记过了，那就是不合法的情况。

在合法的情况下，只有这些入度为0的点才能作为第一批行动的点。从这些点出发， dfs 一遍，把他们能占领的点都标记一下是被谁占领的，就相当于给每个连通块染色了。

染色结束以后，再重新考虑所有有冲突的点，这个时候可以建一个图，在这个图上跑拓扑排序。注意这个新图在建图的时候，只在所有第一批行动的点之间连边。所以原来输入的时候的点号是不能直接用的，要根据输入的点，查一下所属的颜色，用颜色作为新图的点号连边。这次跑的拓扑排序可以决定所有第一批行动点的行动顺序。如果这些点的行动顺序没有环，就可以输出了。

输出完第一批行动点以后，剩余那些被占领掉的点跟在后面输出就行了，顺序无所谓，反正他们都不会有任何作用。

代码非常丑陋，写完直接就 AC 了，都没有好好整理一下：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>

using namespace std;
typedef long long ll;
const ll MAXN = 2e4 + 5;
const ll MOD = 1e9 + 7;

//用链式前向星存没有冲突的边
struct Edge {
    int v, next;
} pool[MAXN * 10];

int head[MAXN], nn;

int n, m, dt, pre[MAXN], low[MAXN], sccCount, sccNo[MAXN];
int us[MAXN * 10], vs[MAXN * 10], os[MAXN * 10];//原始输入的图
stack<int> s;
vector<int> scc[MAXN];//每个scc里面的点号

void addEdge(int u, int v) {
    pool[++nn].v = v;
    pool[nn].next = head[u];
    head[u] = nn;
}

void tarjan(int u) {
    pre[u] = low[u] = ++dt;
    s.push(u);
    for (int i = head[u]; i; i = pool[i].next) {
        int v = pool[i].v;
        if (pre[v] == 0) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (sccNo[v] == 0) {
            low[u] = min(low[u], pre[v]);
        }
    }
    if (pre[u] == low[u]) {
        vector<int> now;
        sccCount++;
        while (true) {
            int t = s.top();
            s.pop();
            sccNo[t] = sccCount;
            scc[sccCount].push_back(t);
            if (t == u) {
                break;
            }
        }
    }
}

int fa[MAXN], root[MAXN];//root表示每个点所属的第一个行动的点号
int occupy[MAXN];//每个连通块是否被占领

int find(int x) {
    if (fa[x] == x) return x;
    return fa[x] = find(fa[x]);
}

void merge(int x, int y) {
    fa[find(x)] = find(y);
}

void dfs(int u, int num) {
    root[u] = num;
    for (int i = head[u]; i; i = pool[i].next) {
        int v = pool[i].v;
        if (root[v] == 0) {
            dfs(v, num);
        }
    }
}

//有冲突的边用邻接表存
vector<int> adj[MAXN];
int in[MAXN];
vector<int> ans;

void topo() {
    queue<int> q;
    for (int i = 1; i <= n; ++i) {
        if (in[i] == 0 && root[i] == i) q.push(i);
    }
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        ans.push_back(u);
        for (int i = 0; i < adj[u].size(); ++i) {
            int v = adj[u][i];
            in[v]--;
            if (in[v] == 0) {
                q.push(v);
            }
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        fa[i] = i;
    }
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &us[i], &vs[i], &os[i]);
        if (os[i] == 0) {
            addEdge(us[i], vs[i]);
            merge(us[i], vs[i]);//用并查集维护不冲突的边组成的连通块
        }
    }
    for (int i = 1; i <= n; i++) {
        if (pre[i] == 0) {
            tarjan(i);
        }
    }
    //跑完强连通以后，先找到所有入度为0的scc
    for (int u = 1; u <= n; ++u) {
        for (int i = head[u]; i; i = pool[i].next) {
            int v = pool[i].v;
            if(sccNo[u]!=sccNo[v]){
                in[sccNo[v]]++;
            }
        }
    }
    int rc = 0;
    for (int i = 1; i <= sccCount; ++i) {
        if (in[i] == 0) {
            rc++;//入度为0的scc的个数
            //这个点可以先行动，一旦它行动，会把整个连通块占领
            int r = find(scc[i][0]);//用这个连通块的根作为代表元
            if (occupy[r] == 1) {
                //如果这个连通块已经被占领了，说明一个连通块里面有不止一个入度为0的点，这样不行
                printf("-1\n");
                return 0;
            }
            occupy[r] = 1;
            dfs(scc[i][0], scc[i][0]);
        }
    }
    memset(in, 0, sizeof in);//入度数组清空，一会儿拓扑还需还需要用一次
    for (int i = 0; i < m; ++i) {
        if (os[i] == 1) {
            int uu = sccNo[us[i]];
            int vv = sccNo[vs[i]];
            adj[root[scc[vv][0]]].push_back(root[scc[uu][0]]);
            in[root[scc[uu][0]]]++;
        }
    }
    topo();
    if (ans.size() != rc) {
        printf("-1\n");
    } else {
        for (int i = 0; i < rc; ++i) {
            printf("%d ", ans[i]);
        }
        for (int i = 1; i <= n; ++i) {
            if (root[i] != i) {
                printf("%d ", i);
            }
        }
    }
    return 0;
}