自动搬运

查看原文

来自洛谷，原作者为

	7KByte **

搬运于2025-08-24 22:35:38，当前版本为作者最后更新于2022-07-19 15:04:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

给定一个 $N\times N$ 的网格，有 $K$ 个格子是障碍，你需要找出最长的螺旋路径。螺旋路径的定义是从一个点出发，向一个方向走最少一格，然后右转 $90$ °，一共右转三次，走了四段，且一格格子最多经过一次，$N\le 1000,K\le 2000$。

不失一般性，我们可以只统计下面这种情况。然后将红线上下分开统计。

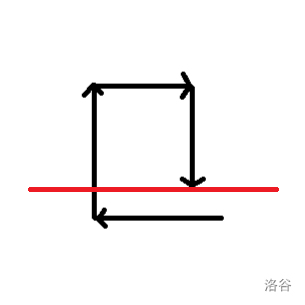
对于红线下面的部分，可以简单 DP 在 $\mathcal{O}(N^2)$ 的时间内完成。

然后考虑红线上面，需要和红线构成一格矩形。那么我们考虑从上到下扫描线。

我们记录 $f(l,r)$ 表示左右边界分别为为 $l,r$ 的拱形的最大长度，那么对于每个障碍物，最多只会对 $N$ 个 $f(l, r)$ 产生影响。那么我们可以用平衡树维护 $f(l, \cdots)$，支持删除一格位置，加入 $\le p$ 的被删除的位置，和查询最小值。

删除是 $\mathcal{O}(\log)$ 的，加入的位置一定被删除过，所以是均摊复杂度，总的时间复杂度是 $\mathcal{O}((N^2 + NK)\log N)$，对于 $4$ 个方向，和翻转之后的方向都要做，所以总时间是 $\mathcal{O}(8(N^2 + NK)\log N)$。

有两个点一直卡不过去，可以 assert 一下数据类型，然后去掉 $8$ 倍常数。

#define N 1005
#define M 2005
int n, m, u[M], v[M], f[N][N], a[N][N], ans;
vector<int>c[N];
struct node{
	int w[N], tag, st;
	multiset<int>s, t;
	void init(int x){
		st = x, tag = 0; 
		s.clear(), t.clear();
		rep(i, x + 1, n)t.insert(i);
	}
	void ins(int p){
		while(!t.empty()){
			int x = *t.begin();
			if(x <= p)t.erase(x), w[x] = x - st + 1 - tag, s.insert(w[x]);
			else break;
		}
	}
	void del(int p){
		if(p <= st || t.find(p) != t.end())return;
		s.erase(s.find(w[p])), t.insert(p);
	}
	int val(){
		if(!s.empty())return *s.rbegin() + tag;
		return 0;
	}
}o[N];
void check(int l,int r){
	if(l > r)return;
	rep(i, l, r - 1)o[i].ins(r);
}
void calc(){
	memset(a, 0, sizeof(a));
	memset(f, 0, sizeof(f));
	rp(i, m)a[u[i]][v[i]] = 1;
	pr(i, n){
		int w = 0;
		pr(j, n)
			if(!a[i][j]){
				w++;
				if(f[i + 1][j])f[i][j] = 1 + f[i + 1][j];
				if(w > 1)cmx(f[i][j], w);
			}
			else w = 0;
	}
	rp(i, n)c[i].clear(), o[i].init(i);
	rp(i, m)c[u[i]].pb(v[i]);
	rp(i, n - 1){
		sort(c[i].begin(), c[i].end());
		go(x, c[i]){
			rp(j, x - 1)o[j].del(x);
			rep(j, x + 1, n)o[x].del(j);
		}
		rp(j, n){
			o[j].tag += 2;
			int cur = o[j].val();
			if(cur && f[i + 1][j])cmx(ans, cur + f[i + 1][j]);
		}
		if(c[i].empty())check(1, n);
		else{
			check(1, c[i][0] - 1), 
			check(c[i][si(c[i]) - 1] + 1, n);
			rp(j, si(c[i]) - 1)check(c[i][j - 1] + 1, c[i][j] - 1);
		}
	}
}
void rotate(){
	rp(i, m){
		int uu = v[i], vv = n - u[i] + 1;
		u[i] = uu, v[i] = vv;
	}
}
int main() {
	read(n, m);
	rp(i, m)read(u[i], v[i]);
	if(n > 990 && m > 1990){
		rotate(), rotate(), rotate();
		rp(i, m)v[i] = n - v[i] + 1;
		rotate(), rotate(), calc(), rotate(), calc();
	}
	else{
		calc();
		rotate(), calc();
		rotate(), calc();
		rotate(), calc();
		rp(i, m)v[i] = n - v[i] + 1;
		calc();
		rotate(), calc();
		rotate(), calc();
		rotate(), calc();
	}
	printf("%d\n", ans);
	return 0;
}