自动搬运

查看原文

来自洛谷，原作者为

	Feyn AFO

搬运于2025-08-24 22:35:28，当前版本为作者最后更新于2022-07-21 11:18:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

link

经典思路，正难则反。一般而言合并两个集合总是比拆分两个集合来得容易的，于是考虑从 $N$ 个散点开始，把删边操作改成加边操作然后统计答案。然后由于是树，每次加边都一定会是合并两个不相交的集合，这样一来就可以用到启发式合并了。

现在剩下的唯一问题就是如何统计答案了。显然两个点在同一个集合内的答案已经累加过了，所以考虑如何求得两个点分属两个集合的方案。由于是启发式合并，考虑先确定小集合内一个点作为方案的一个点，然后思考如何快速求得大集合内有多少点可以和这个点配对即可。放个图：

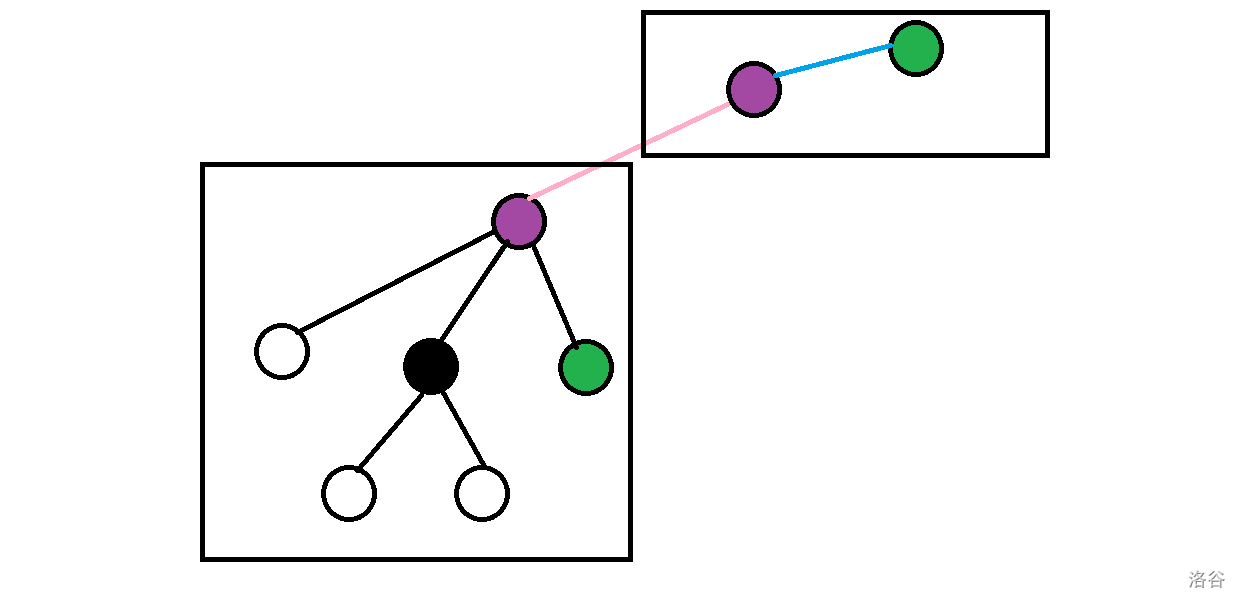
个人感觉挺简单明了的。紫色是合并的两个点，绿色是一种合法的方案，两个框框自然是两个还未合并的集合啦。

当我吗遍历小集合的时候可以轻松求得上紫点到上绿点的异或值，假设为 $A$ 。假设粉边是 $B$，那么一个合法的下绿点应该满足它到下紫点的路径异或和 $C=A\oplus B$ 。现在问题来了，咋快速地求 $C$ 的值呢？重新遍历一遍还不如打暴力。为了解决这个问题，我们假设已经求得了下绿点到黑点的值（怎么求得后面说） $D$ 和下紫点到黑点的值 $E$ ，根据异或的基本性质显然有 $C=D\oplus E$，那么我们希望求的东西就转变成了满足 $D_i\oplus E=A\oplus B$，即 $D_i=A\oplus B\oplus E$ 的 $i$ 的个数，这就可以直接用 map 来统计了。

然后呢考虑前面留下的问题，怎么求出每个点到黑点的值呢？已知紫点到黑点的值和紫点到上绿点的值可以很容易求得黑点到上绿点的值，这可以在遍历小集合的时候求出。所以发现每次合并都相当于是求出每个新加入集合的点到黑点的值，这样就可以快速求解啦。

复杂度 $O(N\log N^2)$。代码还是挺好写的。

#include<bits/stdc++.h>
//#define feyn
#define int long long
const int N=100010;
using namespace std;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar();}
    wh*=f;return;
}
inline void swap(int &s1,int &s2){
	int s3=s1;s1=s2;s2=s3;return;
}

int m,sk[N],an[N],ans;
struct node{
	int a,b,val;
}se[N];

struct edge{
	int t,v,next;
}e[N<<1];
int head[N],esum;
inline void add(int fr,int to,int val){
	e[++esum]=(edge){to,val,head[fr]};head[fr]=esum;
}

int f[N];
inline int find(int wh){
	return f[wh]==wh?wh:f[wh]=find(f[wh]);
}

map<int,int>d[N];
int dis[N],size[N];
inline void dfs(int wh,int now_dis,int fa,int data,int pl){
	dis[wh]=now_dis^data;ans+=d[pl][dis[wh]];
	for(int i=head[wh],th;i;i=e[i].next){
		if((th=e[i].t)==fa)continue;
		dfs(th,(now_dis^e[i].v),wh,data,pl);
	}
}
inline void add_data(int wh,int fa,int pl){
	d[pl][dis[wh]]++;
	for(int i=head[wh],th;i;i=e[i].next){
		if((th=e[i].t)==fa)continue;
		add_data(th,wh,pl);
	}
}

signed main(){
	
	#ifdef feyn
	freopen("in.txt","r",stdin);
	#endif
	
	read(m);
	for(int i=1;i<=m;i++)f[i]=i,size[i]=1,d[i][0]=1;
	for(int i=1;i<m;i++){
		read(se[i].a);read(se[i].b);read(se[i].val);
	}
	for(int i=1;i<m;i++)read(sk[m-i+1]);
	for(int i=2;i<=m;i++){
		int j=i;i=sk[i];
		int a=se[i].a,b=se[i].b;
		//printf("now:%lld %lld %lld\n",a,b,se[i].val);
		int fa=find(a),fb=find(b);
		if(size[fa]<size[fb])swap(a,b),swap(fa,fb);
		f[fb]=fa;size[fa]+=size[fb];d[fb].clear();
		
		int dd=dis[a];
		dfs(b,0,0,dd^se[i].val,fa);
		add_data(b,0,fa);
		add(a,b,se[i].val);add(b,a,se[i].val);
		an[j]=ans;i=j;
	}
	for(int i=m;i;i--)printf("%lld\n",an[i]);
	
	return 0;
}