自动搬运

查看原文

来自洛谷，原作者为

	囧仙 你做东方鬼畜音MAD，好吗？

搬运于2025-08-24 22:35:08，当前版本为作者最后更新于2021-11-19 20:16:14，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

$\small\textbf{Subtask 1}$

直接根据题目当中的式子进行计算。

当然了，如果你采用了「枚举子树」后「分别枚举 $i,j,k$」，并且「花费 $\mathcal O(n)$ 复杂度暴力计算 $\mathrm{lca}$」，时间复杂度将会达到 $\mathcal O(n^5)$，可能不大能过去。一种 $\mathcal O(n^4)$ 的做法是，首先枚举根 $r$，再花费 $\mathcal O(n^3)$ 复杂度算出两两节点之间以 $r$ 为根时的 $\mathrm{lca}$ 值。这些都预处理完后（时间复杂度为 $\mathcal O(n^4)$），再花费 $\mathcal O(n^4)$ 的复杂度暴力枚举，总复杂度是 $\mathcal O(n^4)$。

$\small\textbf{Subtask 2}$

这个 $\mathrm{Subtask}$ 是给暴力进行换根 $\textrm{dp}$ 的选手的。

为了方便起见，记 $\mathit{siz}(u)$ 表示以 $u$ 为根的子树的大小，$\mathit{son}(u)$ 表示直接与 $u$ 相连的子树节点的集合，$\mathit{sub}(u)$ 表示 $u$ 的子树内的所有节点（包含 $u$）构成的集合。

考虑计算 $\mathrm{LCAS}(r)$。那么我们需要 $T_r$ 当中，以每个节点为根时计算出的 $\mathrm{lca}$ 的贡献。不妨设，

$$\mathrm{LCAS}'(u)=\sum_{i\in \mathit{sub}(r)}\sum_{j\in \mathit{sub}(r),j<i} w_{\mathrm{lca}(u,i,j)} $$

运用换根 $\textrm{dp}$ 的思路，首先是要计算出 $\mathrm{LCAS}'(r)$。于是设：

$$\mathrm{LCAS}''(u)=\sum_{i\in \mathit{sub}(u)}\sum_{j\in \mathit{sub}(u),i<j} w_{\mathrm{lca}(r,i,j)} $$

那么 $\mathrm{}$假设现在已经计算出了 $u$ 的所有子树对应的 $\mathrm{LCAS}''$ 值。现在需要将它们合并计算出 $\mathrm{LCAS}''(u)$。于是有：

$$\mathrm{LCAS}''(u)=\sum_{v\in\mathit{son}(u)}\mathrm{LCAS}''(v)+\frac{1}{2}(\mathit{siz}(u)-\mathit{siz}(v))\cdot \mathit{siz}(v)\cdot w_u $$

感性理解一下，就是对子树的 $\mathrm{LCAS}''$ 求和，接着考虑以 $u$ 为 $\mathrm{lca}$ 时产生的贡献。这部分贡献来自于一棵子树内的节点与其他节点组成的 $\mathrm{lca}$。因为要考虑先后顺序，因此最后要除以 $2$。

那么就能计算出，$\mathrm{LCAS}'(r)=\mathrm{LCAS}''(r)$。现在考虑从 $\mathrm{LCAS}'(r)$ 开始向它的子树推进。

假设已经计算出了 $\mathrm{LCAS}'(u)$，现在要推向它的一个直接儿子作为新的根。那么就要考虑一些节点有序对的 $\mathrm{lca}$ 由 $u$ 转变为了 $v$。这部分有序对肯定有一元在 $T_v$ 当中，另外一元在 $\complement _{\mathit{sub}(r)}T_v$ 当中。于是，

$$\mathrm{LCAS}'(v)=\mathrm{LCAS}'(u)-(w_u-w_v)\cdot \mathit{siz}(v)\cdot (\mathit{siz}(r)-\mathit{siz}(v)) $$

然后就能计算出 $T_r$ 当中每个节点的 $\mathrm{LCAS}'$ 的值。相加得到 $\mathrm{LCAS}(r)$。

容易发现这样子计算一棵子树的时间复杂度为 $\mathcal O(n)$，那么计算所有子树的时间复杂度为 $\mathcal O(n^2)$。

$\small\textbf{Subtask 3,4}$

大概有特殊规律吧，我没找过。

$\small\textbf{Subtask 5}$

考虑如何计算大小为 $n$ 的子树 $T$ 的 $\mathrm{LCAS}$ 的值。

同 $\textrm{Subtask 2}$，记 $\mathit{siz}(u)$ 表示以 $u$ 为根的子树的大小，$\mathit{son}(u)$ 表示直接与 $u$ 相连的子树节点的集合，$\mathit{sub}(u)$ 表示 $u$ 的子树内的所有节点（包含 $u$）构成的集合。

为了方便计算，我们可以去除 $j,k$ 之间的大小关系。

$$\begin{aligned} \mathrm{LCAS}_0(u)&=\sum_{i\in\mathit{sub}(u)}\sum_{j\in\mathit{sub}(u)}\sum_{k\in\mathit{sub}(u)}w_{\operatorname{lca}(i,j,k)} \cr \mathrm{LCAS}(u)&=\frac{1}{2}\left(\mathrm{LCAS}_0(u)-\mathit{siz}(u)\cdot \sum_{v\in \mathit{sub}(u)} w_v\right) \end{aligned} $$

此外，我们还定义：

$$\mathrm{LCAS}_1(u)=\sum_{i\in\mathit{sub}(u)}\sum_{j\in\mathit{sub}(u)} w_{\operatorname{lca}(u,i,j)} $$

为了方便计算，我们还要定义另外一个东西 $\mathrm{LCAS}_2(u)$。它的含义是，在根部新增一个节点，树根在子树 $u$ 内，会使答案新增加的值。也就是，

$$\mathrm{LCAS}_2(u)=\sum_{i\in\mathit{sub}(u)}\sum_{j\in\mathit{sub}(u)} w_{\operatorname{lca}(i,u,j)} $$

一种比较常见的树形 $\text{dp}$ 的想法是，计算出每棵子树的答案后，再合并到根节点。不过这里为了方便，采用了「合并根节点和第一棵子树、合并第二棵子树、第三棵子树……」这样的做法。

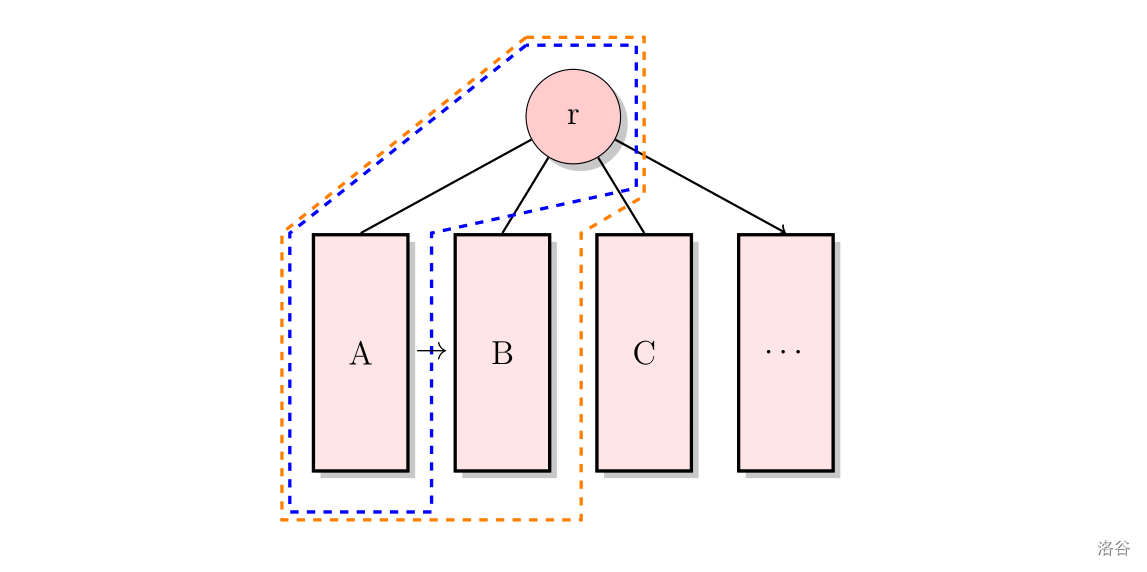
现在假设要处理根为 $u$ 的子树的答案。我们要做的就是不断把右边一个递归计算好 $\mathrm{LCAS}_0,\mathrm{LCAS}_1,\mathrm{LCAS}_2$ 的值的连通块塞到它左边的连通块里，并且不断维护新的连通块的 $\mathrm{LCAS}_0(u),\mathrm{LCAS}_1(u),\mathrm{LCAS}_2(u)$，假设下一个要合并的子树的根节点为 $v$。

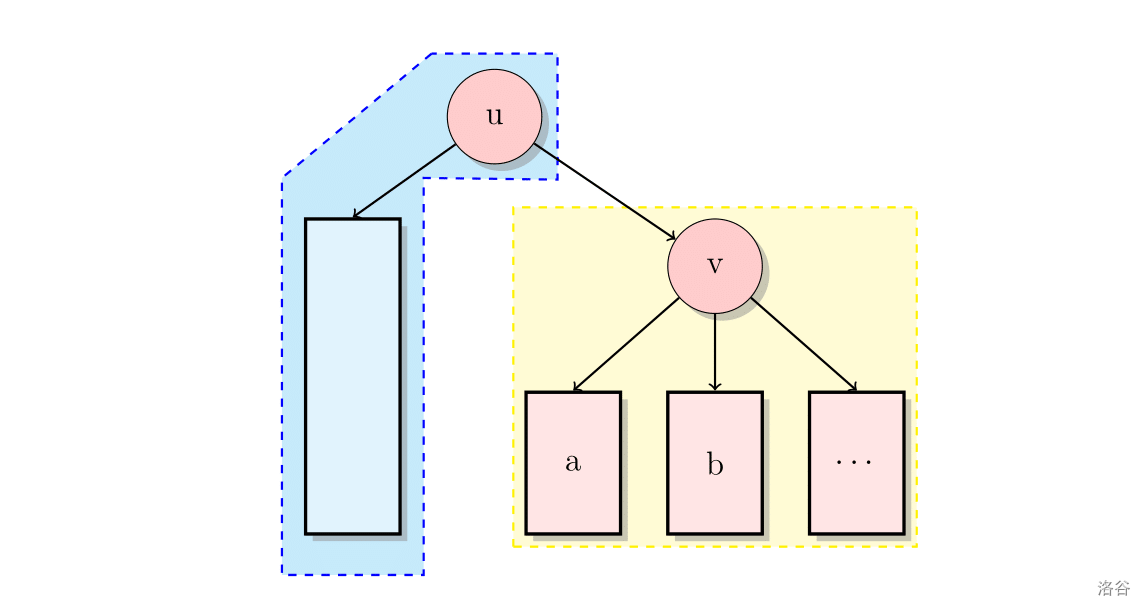
下面不妨记蓝色区域为区域 $A$，黄色区域为区域 $B$。由于我们要计算的式子里有 $i,j,k$ 三个变量，因此下文分类讨论时就说他们的取值范围了。

$\mathbf{LCAS_0}$

• 第一种情况：根节点 $i$ 在 $A$ 当中。
  • $j,k$ 都在 $A$ 当中，这部分的贡献显然就是 $\mathrm{LCAS}_0(u)$。
  • $j$ 在 $A$ 当中，$k$ 在 $B$ 当中。容易发现，$k$ 无论在 $B$ 的哪里，它的地位都等同于 $u$ 节点的位置。因此这部分的贡献是 $\mathrm{LCAS}_2(u)\cdot \mathit{siz}(v)$。
  • $k$ 在 $A$ 当中，$j$ 在 $B$ 当中。这一部分的贡献和上一部分是一致的（因为相当于交换了两者的顺序），因此贡献还是 $\mathrm{LCAS}_2(u)\cdot \mathit{siz}(v)$。
  • $j,k$ 都在 $B$ 当中，容易发现此时的 $i$ 的地位和 $v$ 等同。因此这部分的贡献是 $\mathrm{LCAS}_1(v)\cdot\mathit{siz}(u)$。
• 第二种情况：根节点 $i$ 在 $B$ 当中。其实这种情况和第一种情况类似，可以如法炮制。
  • $j,k$ 都在 $A$ 当中。同上文，答案是 $\mathrm{LCAS}_1(u)\cdot\mathit{siz}(v)$。
  • $j,k$ 都在 $B$ 当中。同上文，答案是 $\mathrm{LCAS}_0(v)$。
  • $j$ 在 $A$ 当中，$k$ 在 $B$ 当中。同上文，答案是 $\mathrm{LCAS}_2(u)\cdot \mathit{siz}(v)$。
  • $k$ 在 $A$ 当中，$j$ 在 $B$ 当中。同上文，答案是 $\mathrm{LCAS}_2(u)\cdot \mathit{siz}(v)$。

通过上述讨论，我们可以得到新的 $\mathrm{LCAS}_0(u)$ 的表达式：

$$\begin{aligned} \mathrm{LCAS}_0(u)\gets& \mathrm{LCAS}_0(u)+2\cdot\mathit{siz}(v)\cdot \mathrm{LCAS}_2(u)+\mathrm{LCAS}_1(v)\cdot\mathit{siz}(u)\cr +& \mathrm{LCAS}_0(v)+2\cdot\mathit{siz}(u)\cdot \mathrm{LCAS}_2(v)+\mathrm{LCAS}_1(u)\cdot\mathit{siz}(v)\cr \end{aligned}$$

初始时 $\mathrm{LCAS}_0(u)=w_u$。

$\mathbf{LCAS_1}$

这部分问题相对而言比较简单。

• 第一种情况，$j,k$ 在 $A$ 当中。容易发现这部分贡献就是 $\mathrm{LCAS}_1(u)$。
• 第二种情况，$j,k$ 在 $B$ 当中。容易发现这部分贡献就是 $\mathrm{LCAS}_1(v)$。
• 第三种情况，$j$ 在 $A$ 当中，$k$ 在 $B$ 当中。此时 $\mathrm{lca}(u,j,k)$ 必然是 $u$，因此容易得到贡献就是 $w_u\cdot\mathit{siz}(j)\cdot \mathit{siz}(k)$。
• 第四种情况，$j$ 在 $B$ 当中，$k$ 在 $A$ 当中。同上，贡献是 $w_u\cdot\mathit{siz}(j)\cdot \mathit{siz}(k)$。

因此，

$$\mathrm{LCAS}_1(u)\gets \mathrm{LCAS}_1(u)+\mathrm{LCAS}_1(v)+2\cdot\mathit{siz}(u)\cdot\mathit{siz}(v)\cdot w_u $$

初始时 $\mathrm{LCAS}_1(u)=w_u$。

$\mathbf{LCAS_2}$

这部分问题也不太难。

• 第一种情况，$i,k$ 都在 $A$ 当中。容易发现可以根据定义得到该部分的贡献是 $\mathrm{LCAS_2}(u)$。
• 第一种情况，$i,k$ 都在 $B$ 当中。此时可以发现，$u$ 的地位和 $v$ 的地位等同，也就是说，$$\sum_{i\in B}\sum_{k\in B} w_{\mathrm{lca}(i,u,k)}=\sum_{i\in B}\sum_{k\in B} w_{\mathrm{lca}(i,v,k)} $$因此贡献是 $\mathrm{LCAS_2}(v)$。
• 第三种情况，$i$ 在 $A$ 当中，$k$ 在 $B$ 当中。此时可以发现 $\mathrm{lca}(i,u,k)=u$，因此贡献是 $w_u\cdot \mathit{siz}(u)\cdot \mathit{siz}(v)$。
• 第四种情况，$i$ 在 $B$ 当中，$k$ 在 $A$ 当中。此时可以发现 $\mathrm{lca}(i,u,k)=u$，因此贡献是 $w_u\cdot \mathit{siz}(u)\cdot \mathit{siz}(v)$。

因此，

$$\mathrm{LCAS}_2(u)\gets \mathrm{LCAS}_2(u)+\mathrm{LCAS}_2(v)+2\cdot\mathit{siz}(u)\cdot\mathit{siz}(v)\cdot w_u $$

初始时 $\mathrm{LCAS}_2(u)=w_u$。

总结

容易发现，$\mathrm{LCAS}_1(u)$ 和 $\mathrm{LCAS}_2(u)$ 的初始值、推导公式一模一样。因此可以得到 $\mathrm{LCAS}_1(u)=\mathrm{LCAS}_2(u)$，你只需要算一个就行了。最后是给出 $\mathrm{LCAS}_0$ 的柿子：

$$\begin{aligned} \mathrm{LCAS}_0(u)\gets& \mathrm{LCAS}_0(u)+3\cdot\mathit{siz}(v)\cdot \mathrm{LCAS}_1(u)\cr +& \mathrm{LCAS}_0(v)+3\cdot\mathit{siz}(u)\cdot \mathrm{LCAS}_1(v)\cr \mathrm{LCAS}_1(u)\gets& \mathrm{LCAS}_1(u)+\mathrm{LCAS}_1(v)+\mathit{siz}(u)\cdot\mathit{siz}(v)\cdot w_u\cr \end{aligned} $$

记得最后把 $\mathrm{LCAS}_0$ 转换成 $\mathrm{LCAS}$。

$$\mathrm{LCAS}(u)=\frac{1}{2}\left(\mathrm{LCAS}_0(u)-\mathit{siz}(u)\cdot \sum_{v\in \mathit{sub}(u) } w_v\right)$$

参考代码

$\small \textbf{Subtask 1}$

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i)
using namespace std;
typedef long long i64;
const int INF =2147483647;
const int MAXN=100+3;
int n,W[MAXN];
int qread(){
    int w=1,c,ret;
    while((c=getchar())> '9'||c< '0') w=(c=='-'?-1:1); ret=c-'0';
    while((c=getchar())>='0'&&c<='9') ret=ret*10+c-'0';
    return ret*w;
}
int H[MAXN],V[MAXN*2],N[MAXN*2],G[MAXN],t;
void add(int u,int v){
    V[++t]=v,N[t]=H[u],H[u]=t;
}
int L[MAXN][MAXN][MAXN],F[MAXN]; bool T[MAXN];
int A[MAXN],B[MAXN],S[MAXN],s;
void dfs(int u,int f){
    S[++s]=u,A[u]=s;
    for(int i=H[u],v;i;i=N[i]) if((v=V[i])!=f) dfs(v,u);
    B[u]=s;
}
const int MOD =998244353;
int main(){
    n=qread(); up(1,n,i) W[i]=qread();
    up(1,n-1,i){
        int u=qread(),v=qread(); add(u,v),add(v,u);
    }
    up(1,n,r){
        memset(F,0,sizeof(F)); F[r]=r; queue <int> Q; Q.push(r);
        while(!Q.empty()){
            int u=Q.front(); Q.pop();
            for(int i=H[u],v;i;i=N[i]) if(!F[v=V[i]]){
                F[v]=u,Q.push(v);
            }
        }
        up(1,n,i) up(1,n,j){
            int u=i,v=j; memset(T,0,sizeof(T));
            while(u!=r) T[u]=true,u=F[u]; T[r]=true;
            while(v!=r) if(T[v]){
                L[r][i][j]=v; goto nxt;
            } else v=F[v];
            L[r][i][j]=r; nxt:;
        }
    }
    dfs(1,0); up(1,n,r){
        int w=0,a=A[r],b=B[r];
        up(a,b,i) up(a,b,j) up(a,b,k) if(S[j]<S[k])
            w=(w+W[L[S[i]][S[j]][S[k]]])%MOD;
        printf("%d\n",w);
    }
    return 0;
}

$\small \textbf{Subtask 2}$

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i)
using namespace std;
typedef long long i64;
const int INF =2147483647; 
const int MAXN=1000+3; 
int qread(){
    int w=1,c,ret;
    while((c=getchar())> '9'||c< '0') w=(c=='-'?-1:1); ret=c-'0';
    while((c=getchar())>='0'&&c<='9') ret=ret*10+c-'0';
    return ret*w;
}
int n,H[MAXN],V[MAXN*2],N[MAXN*2],t;
void add(int u,int v){
    V[++t]=v,N[t]=H[u],H[u]=t;
}
const int MOD =998244353;
int S[MAXN],W[MAXN],X[MAXN],F[MAXN];
void dfs0(int u,int f){
    F[u]=f;
    for(int i=H[u],v;i;i=N[i]) if((v=V[i])!=f) dfs0(v,u); 
}
void dfs1(int u,int f){ 
    for(int i=H[u],v;i;i=N[i]) if((v=V[i])!=f){
        dfs1(v,u);
        X[u]=(1ll*W[u]*S[v]%MOD*S[u]+X[v]+X[u])%MOD,S[u]+=S[v];
    }
    X[u]=(1ll*W[u]*S[u]+X[u])%MOD,++S[u];
}
int r;
void dfs2(int u,int f){
    r=(r+X[u])%MOD;
    for(int i=H[u],v;i;i=N[i]) if((v=V[i])!=f){
        X[v]=((-1ll*(W[u]-W[v]+MOD)*(S[u]-S[v]+MOD)%MOD
                *S[v]+X[u])%MOD+MOD)%MOD;
        S[v]=S[u],dfs2(v,u);
    }
}
int main(){
    n=qread(); up(1,n,i) W[i]=qread();
    up(1,n-1,i){
        int u=qread(),v=qread(); add(u,v),add(v,u);
    }
    dfs0(1,0);
    up(1,n,i){
        memset(S,0,sizeof(S));
        memset(X,0,sizeof(X));
        dfs1(i,F[i]),dfs2(i,F[i]);
        printf("%d\n",r),r=0;
    }
    return 0;
}

$\small \textbf{Subtask 5}$

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i)
using namespace std;
typedef long long i64;
const int INF =2147483647;
const int MAXN=1e6+3,MAXM=MAXN*2;
const int MOD =998244353,DIV2=499122177;
int n,A[MAXN],S0[MAXN],S1[MAXN],W[MAXN],T[MAXN];

namespace Gra{
    int H[MAXN],V[MAXM],N[MAXM],S[MAXN],t;
    void add(int u,int v){V[++t]=v,N[t]=H[u],H[u]=t;}
    void dfs(int u,int f){
        S0[u]=S1[u]=T[u]=W[u],S[u]=1;
        for(int i=H[u],v;i;i=N[i]) if((v=V[i])!=f){
            dfs(v,u); int s0=0,s1=0;
            s0=(1ll*S0[u]+3ll*S[v]*S1[u]%MOD
               +1ll*S0[v]+3ll*S[u]*S1[v]%MOD)%MOD;
            s1=(1ll*S1[u]+S1[v]+2ll*W[u]*S[u]%MOD*S[v]%MOD)%MOD;
            S0[u]=s0,S1[u]=s1,S[u]+=S[v],T[u]=(T[u]+T[v])%MOD;
        }
        A[u]=1ll*(1ll*S0[u]-1ll*S[u]*T[u]%MOD+MOD)*DIV2%MOD;
    }
}
int qread(){
    int w=1,c,ret;
    while((c=getchar())> '9'||c< '0') w=(c=='-'?-1:1); ret=c-'0';
    while((c=getchar())>='0'&&c<='9') ret=ret*10+c-'0';
    return ret*w;
}
int main(){
    n=qread(); up(1,n,i) W[i]=qread();
    up(1,n-1,i){
        int u=qread(),v=qread(); Gra::add(u,v),Gra::add(v,u);
    }
    Gra::dfs(1,0);
    up(1,n,i) printf("%d\n",A[i]);
    return 0;
}