自动搬运

查看原文

来自洛谷，原作者为

	囧仙 你做东方鬼畜音MAD，好吗？

搬运于2025-08-24 22:35:08，当前版本为作者最后更新于2021-11-19 14:41:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题解

容易发现，对多边形以及其中的斜线进行旋转并不会对答案造成任何影响。因此第一步可以将所有斜线旋转至水平，便于进行下一步讨论。

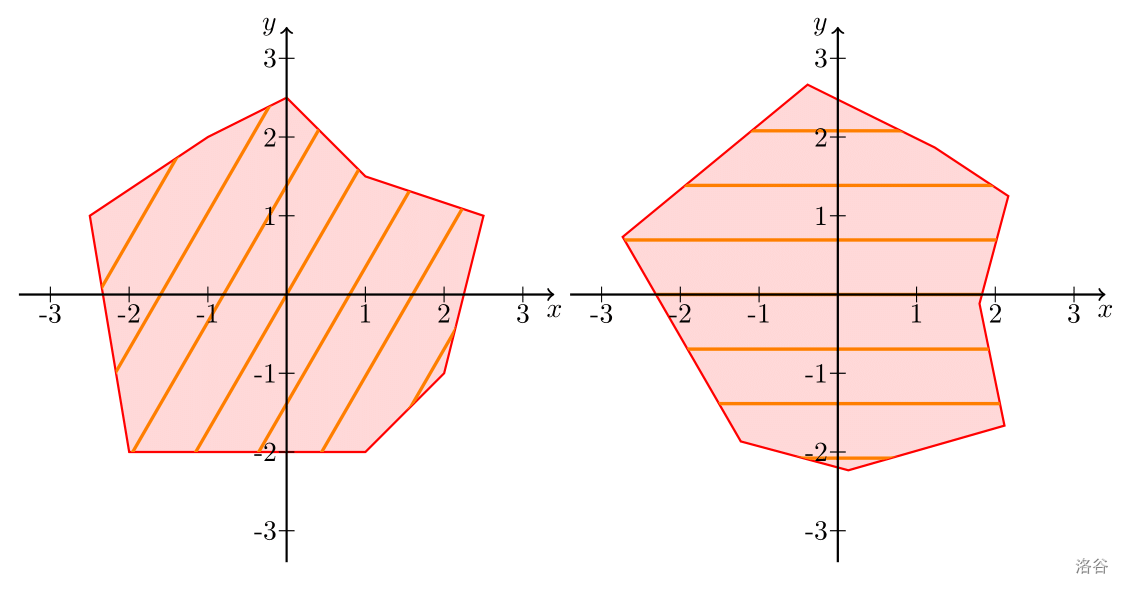
（这里用了样例 $2$ 的图）

关于线段的旋转，这里提供两种思路：

• 第一种思路是，将笛卡尔坐标系转为极坐标系，让极角加上需要旋转的角度后再转换回来。具体而言，对于点 $(x_0,y_0)$，它的极径为 $r=\sqrt{x_0^2+y_0^2}$，极角为 $\theta=\arctan \dfrac{y_0}{x_0}$（关于极角的计算，可以使用 $\text{C++}$ 中的函数 $\verb!atan2(y,x)!$，注意 $\bm x$ 坐标和 $\bm y$ 坐标的顺序）。将极坐标 $(r,\theta)$ 转换为笛卡尔坐标系中的坐标，即为 $(r\cdot \cos\theta,r\cdot \sin \theta)$。
• 第二种思路是，把平面看成复平面，利用复数乘法「辐角相加，模长相乘」的特点，把 $x_0+\mathrm iy_0$ 乘上辅角为 $\theta$，模长为 $1$ 的复数 $\cos\theta+\mathrm i\sin\theta$。

不旋转坐标系，直接硬上应该也行；我没试过。

---

容易发现，一条橙色线段可以认为是从右侧某条方向向下的线段发出、打到了左侧某条方向向上的线段上的。因此不妨考虑差分的思想：

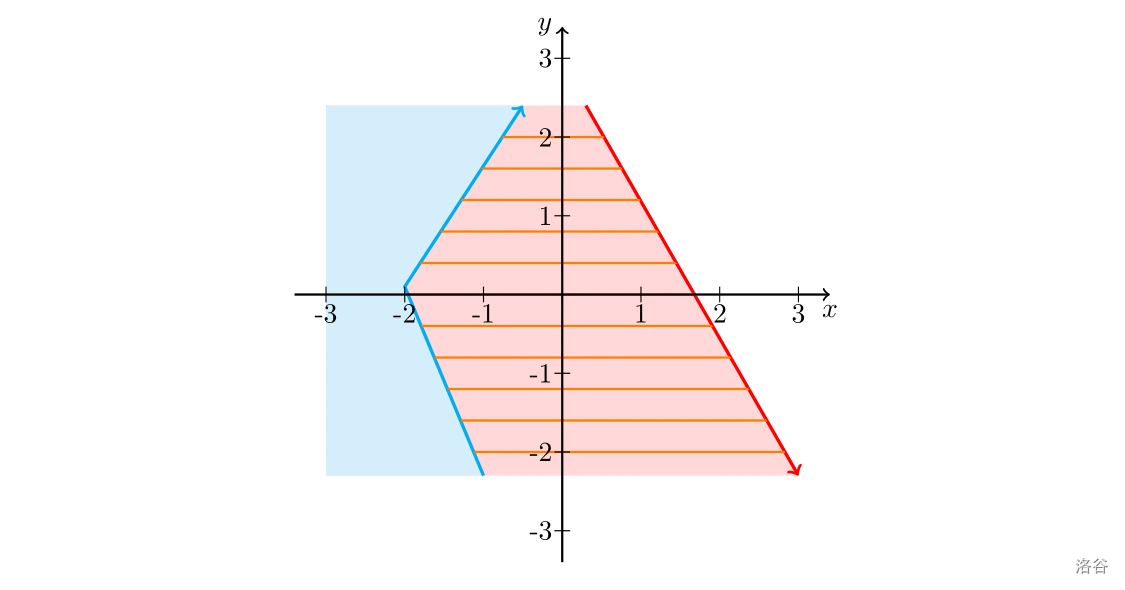
以顺时针为正方向，在左侧随便取个竖直线段作为基准线，计算由红色线段向基准线发出的所有橙色线段的长度之和。方向向下时对答案的贡献为正，方向向上时对答案的贡献为负。容易发现，两者之和就是这两条线段之间的橙色线段长度之和。因此问题简化为了，计算一条线段发出来的到达左侧基准线的橙色线段的长度之和。

由于题目中保证了斜线不会与多边形的任何边平行，因此可以认为红色线段的斜率必然不为 $0$。设线段的两个端点为 $A(x_1,y_1)$ 和 $B(x_2,y_2)$。可以计算出斜线两两之间的距离 $d=a\sin\theta$，那么橙色线段都可以表示为 $y=kd,k\in \Bbb Z$。由于 $y_1<kd<y_2$，因此可以解出 $k$ 的最小值为 $\left\lceil\dfrac{y_1}{d}\right\rceil$，最大值为 $\left\lfloor\dfrac{y_2}{d}\right\rfloor$（这里并不需要强调 $kd$ 与 $y_1,y_2$ 是否可以相等，因为你可以给每个点加上个微小的 $y$ 方向偏移量如 $10^{-9}$，来避开此类问题）。

现在要做的，是根据线段 $AB$ 的解析式算出 $k$ 最小、最大的情况下的 $x$ 坐标。

$$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} \Rightarrow x=\frac{x_2-x_1}{y_2-y_1}(y-y_1)+x_1 $$

因为基准线可以随便取，因此这里直接取 $y$ 轴作为基准线。计算出 $x_{\mathrm{left}}$ 和 $y_{\mathrm{right}}$ 后可以使用等差数列求和进行计算。已知起始值、终止值、项数（$t=\dfrac{|y_1-y_2|}{d}$），那么有：

$$\text{贡献}=\frac{(x_{\mathrm{left}}+x_{\mathrm{right}})\cdot t}{2} $$

（事实上，如果 $y_1>y_2$ 就能说明贡献为正；如果 $y_1<y_2$ 就能说明贡献为负。因此在计算 $t$ 的时候去掉绝对值就能考虑到贡献的正负）。

统计所有边的贡献即可得到答案。

参考代码

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i)
using namespace std;
typedef long long i64;
const int INF =2147483647;
const int MAXN=1e6+3;
int n; double X[MAXN],Y[MAXN],a,o,ans;
int main(){
    size_t w;
    scanf("%d",&n); up(1,n,i) scanf("%lf%lf",&X[i],&Y[i]);
    scanf("%lf%lf",&o,&a),o=o/180*acos(-1),a=a*sin(o);
    up(1,n,i){
        double x=X[i],y=Y[i];
        double l=sqrt(pow(x,2)+pow(y,2)),b=atan2(y,x);
        b-=o,x=l*cos(b),y=l*sin(b),X[i]=x-1e-9,Y[i]=y-1e-9;
    }
    X[n+1]=X[1],Y[n+1]=Y[1];
    up(1,n,i){
        double u,v;
        if(Y[i]<Y[i+1]) u=ceil(Y[i  ]/a)*a,v=floor(Y[i+1]/a)*a;
        else            u=ceil(Y[i+1]/a)*a,v=floor(Y[i  ]/a)*a;
        double x,y,w=(v-u)/a+1;
        x=(u-Y[i])/(Y[i+1]-Y[i])*(X[i+1]-X[i])+X[i];
        y=(v-Y[i])/(Y[i+1]-Y[i])*(X[i+1]-X[i])+X[i];
        if(Y[i]>Y[i+1]) ans+=(x+y)*w/2;
        else            ans-=(x+y)*w/2;
    }
    printf("%.10lf\n",ans);
    return 0;
}