自动搬运

查看原文

来自洛谷，原作者为

	囧仙 你做东方鬼畜音MAD，好吗？

搬运于2025-08-24 22:35:07，当前版本为作者最后更新于2021-11-19 14:13:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解

首先给出结论：方案合法，当且仅当左括号数目和右括号数目相等。

考虑非常套路地，将左括号记为 $+1$，右括号记为 $-1$。那么一段括号序列可以被看做是一条折线，碰到左括号就向上走 $1$ 个单位，碰到右括号就向下走一个单位。

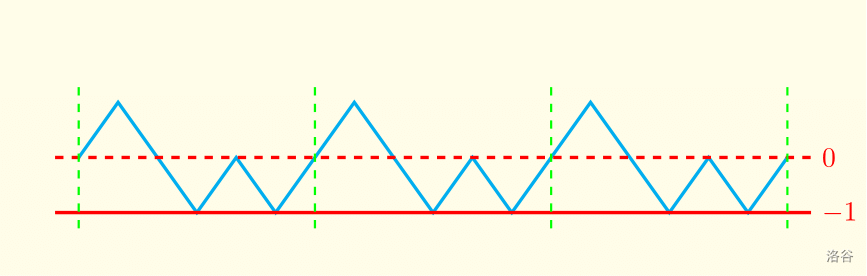
这张图对应的 $S_0=\verb!())()(!$。容易发现，如果左括号数目和右括号数目相同，那么折线就会出现循环节，并且总是能在一个循环节里找到一个最低的位置。那么再选定无穷次循环后的折线的最低点，它们之间形成的括号序列就是无限长的合法括号序列。

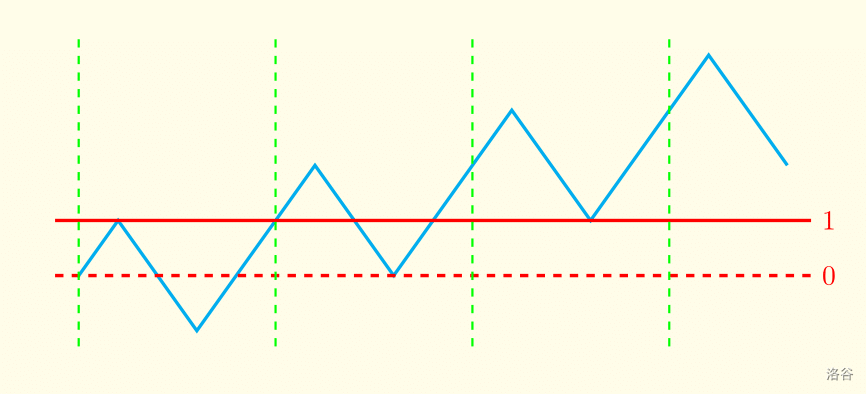
这张图对应的 $S_0=\verb!())((!$。容易发现，如果左括号数目和右括号数目不相同，那么整条折线就会有向上/向下的趋势（每次循环后，折线总体的高度至少改变一个单位）。那么我们无论如何是找不到一条线段能够经过无穷个折线的，因此必然不合法。

现在假设有 $u$ 个左括号，$v$ 个右括号，$w$ 个问号。已知合法方案里左括号和右括号数目相同，因此假设 $x$ 个问号替换成了左括号，$y$ 个问号替换成了右括号，就有：

因此可以解出，$x=\dfrac{v+w-u}{2}$。那么答案就是 $\dbinom{w}{x}$，记得判一下无论如何都不能让左右括号数目相等的情况。

参考代码

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i)
using namespace std;
typedef long long i64;
const int INF =2147483647;
const int MAXN=1e5+3;
const int MOD =998244353;
int n,a,b,c; char S[MAXN];
int pwr(int x,int y){
    int r=1; while(y){
        if(y&1) r=1ll*r*x%MOD; x=1ll*x*x%MOD,y>>=1; 
    }
    return r;
}
int chs(int x,int y){
    if(y<0||y>x) return 0;
    int r=1,s=1,t=1; up(1,x,i){
        r=1ll*r*i%MOD; if(i==y) s=r; if(i==x-y) t=r;
    }
    return 1ll*r*pwr(s,MOD-2)%MOD*pwr(t,MOD-2)%MOD;
}
int main(){
    scanf("%d%s",&n,S+1);
    up(1,n,i) switch(S[i]){
        case '(': ++a; break;
        case ')': ++b; break;
        case '?': ++c; break;
    }
    printf("%d\n",n%2==0?chs(c,(c+b-a)/2):0);
    return 0;
}