自动搬运

查看原文

来自洛谷，原作者为

	柳下惠 与君相别离，不知何日是归期，我如朝露转瞬晞

搬运于2025-08-24 22:35:02，当前版本为作者最后更新于2021-12-26 22:11:51，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

原题链接。

前置知识：

方差计算公式。

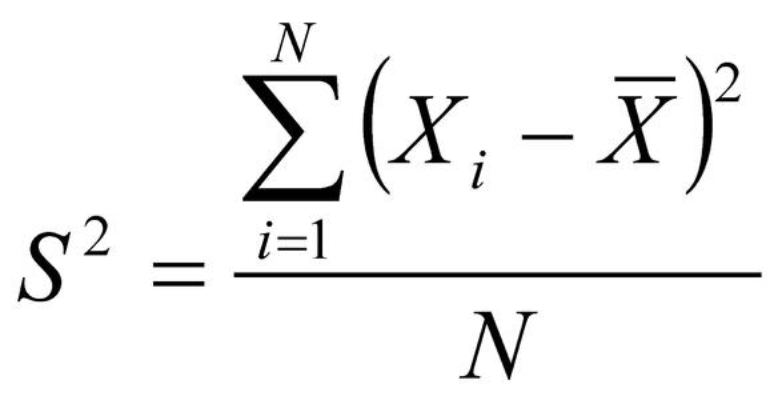
题目大意：

给你一段序列和一个值 $k$，求出一个最小的 $x$ 使这个序列上每个值都乘 $x$ 后的序列方差值与 $k$ 相差最小。

分析：

根据数学原理，如果一个数 $×a$后，原方差 $s^2$ 就会变为 $s^2×a×a$。

我们可以先求出原序列的方差 $s^2$，所以在最好的情况下 $k=s^2×a×a$，所以 $a=sqrt(k/s^2)$，此时不难证明最优值为 $a$，但因为精度，直接开方出来的 $a$ 不一定是最优值，此时还需在一定范围内进行判断。

code:

#include<bits/stdc++.h>
#define I using
#define her std
#define ll long long
#define Love namespace
#define very_much ;
I Love her very_much//防伪
const int maxn=7*1e6+5;
ll n,m,k;
double p=0,s=0;
double a[maxn];
double minn=1e21;//需赋极大值
ll read()
{
	ll x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
int main()
{
	n=read(),k=read();
	for(int i=1;i<=n;i++) a[i]=read();
	sort(a+1,a+1+n);//排序进行特判
	if(a[1]==a[n]) //如果最大值等于最小值，显然方差为0
	{
		printf("No answer!");
		return 0;
	}
	for(int i=1;i<=n;i++) p+=a[i];
	p/=n;
	for(int i=1;i<=n;i++) s+=(a[i]-p)*(a[i]-p);
	s/=n;//计算出原方差
	ll ans=sqrt(k/s);//求出可能的最优值
	for(double i=max(1.0,ans-6.0);i<=ans+6.0;i+=1.0)//最优值会在一定范围内波动
	{ 
		if(abs(s*i*i-k)<minn)//如果此时的i会使s更接近k
		{
			minn=abs(s*i*i-k);//进行替换
			ans=i;
		}
	}
	printf("%lld",ans);//输出
}