自动搬运

查看原文

来自洛谷，原作者为

	泥土笨笨 《算法竞赛实战笔记》作者

搬运于2025-08-24 22:34:57，当前版本为作者最后更新于2021-12-24 15:11:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

今年和学生们一起在机房一起比(tui)赛(fei)，银组三道题都写了，写个题解纪念一下吧。

第一想法是，如果用 $f_i$ 数组表示敌人的牛的位置，一共 %m% 头敌人的牛，可以把整个数轴划分为 $m+1$ 个区间，那么每个区间互不影响，可以单独考虑。比如目前我们考虑 $f_i$ 到 $f_{i+1}$ 这个区间。那么如果在 $f_i$ 左侧放一头自己的牛，这头自己的牛不会影响到 $f_i$ 到 $f_{i+1}$ 这个区间内部的草，因为 $f_i$ 位置敌人的牛离这些草更近。同理，如果在 $f_{i+1}$ 右侧放自己的牛，也不会影响这个区间内部的草。所以我们可以把每个区间单独考虑。

当然， $f_1$ 左侧所有的草，如果我们想要的话，只需贴着 $f_1$ 左边一点点，放我们自己的牛，即可全部收入囊中。同理, $f_m$ 右侧的草，也只需要一头牛即可全部搞定。那么对于每个区间内部的草呢？

先发现一个结论，就是每个区间内部最多放两头牛，就能占掉所有的草。比如下图中所有的草用 $p$ 表示，我们只需把自己的牛放在 $c_1$ 和 $c_2$ 的位置，就能收获所有这个区间内的草。也就是说，每个区间最多放两头牛。

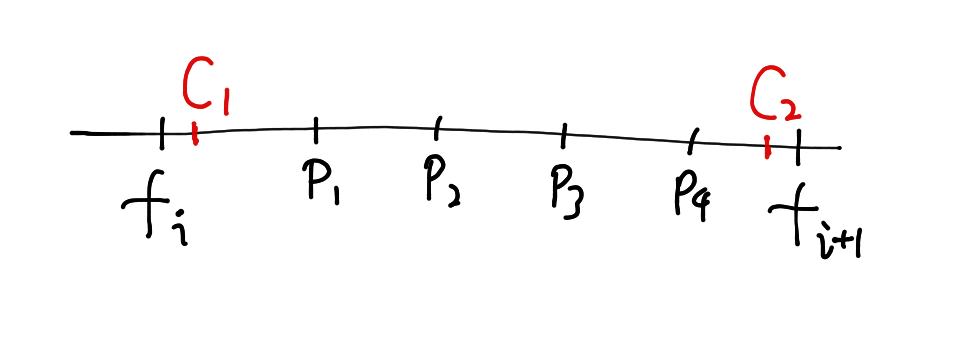
下一步考虑，如果这个区间只放一头牛呢？最大收益是多少？首先我们观察有多少个不同的放牛的位置。对于每块草地，它到区间的左右边界的最小值，叫做这个草地的半径，只要我们把牛放在这个半径以内，我们就可以占领这块草，比如下图，对于每个草地，我们把半径画出来。并且把每个区域与这个区间内的交点，用大家最喜欢的黄色标出来，称之为关键点：

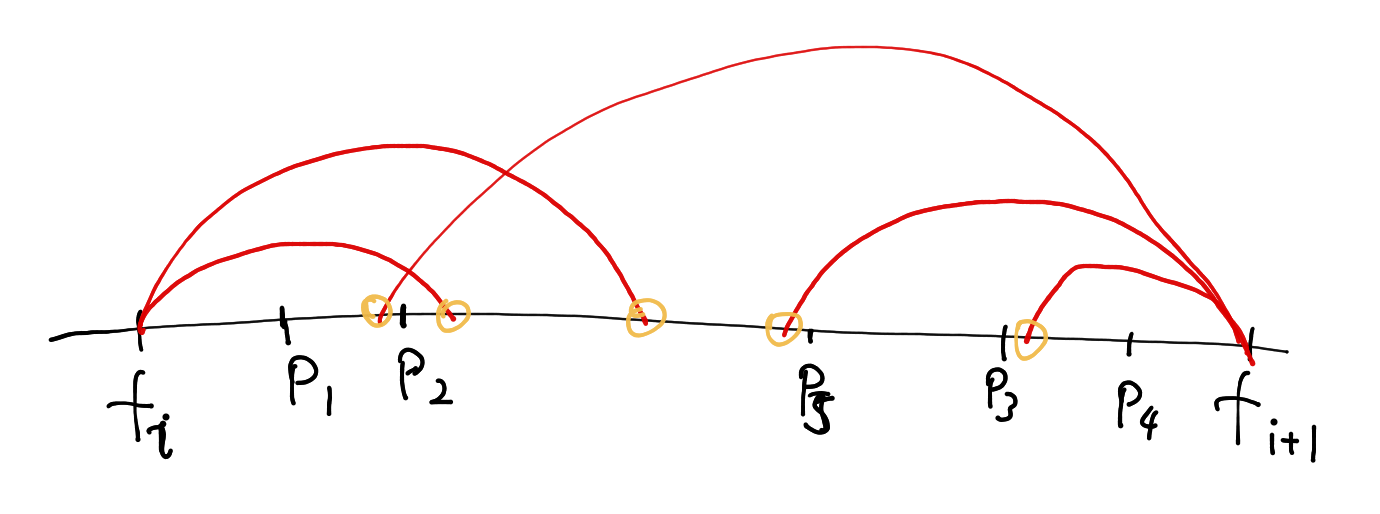
可以发现，在相邻关键点之间，牛放在什么位置是无所谓的，所以不妨认为牛放在每个关键点左边一点点的位置。但是从一个关键点，走到下一个关键点，能控制的牛的数量就会发生变化了。这里可以用滑窗或者尺取类似的思路，维护一个范围 $left$ 到 $right$ ，是当前位置放牛，可以控制的草的范围。每当牛走到下一个位置的时候，如果发现 $left$ 已经脱离范围了，就把 $left++$ ，如果发现 $right+1$ 进入范围了，就把 $right++$ ，这样我们在 $O(n)$ 时间内能算出来任何一个位置放牛的收益。

好了，现在问题模型已经转化了。变成有 $m+1$ 个区间，每个区间放一头牛的收益记为 $value_i$ ，放两头牛的收益记为 $all_i$ ，总共有 $n$ 头牛，问总收益虽大是多少。

这个问题我们可以用贪心解决。开一个优先队列，把每个区间放进去，优先队列按照当前区间再放一头牛的收益，从大到排序。这样我们相当于每次决策的时候，都选择一个最划算的区间，尽量用手里现在这头牛，获得最大的价值。当一个区间从优先队列里面取出来的时候，我们看一下，如果这个区间是第一次被取出来，我们就把它的 $value$ ，改成 $all-value$ 再放回去。表示这个区间已经放过一头牛了，如果再放一头牛，它的价值就是放两头牛价值的总和，那么第二头牛的价值就是 $all-value$ 。这样一直贪心就可以了。

赛时代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>

using namespace std;
typedef long long ll;
const ll MAXN = 2e5 + 5;

struct Grass {
    ll p, t;//位置，价值
    ll l, r;//想占据当前草地，需要放牛的区间，都是开区间
    bool operator<(const Grass &a) const {
        return p < a.p;
    }
} g[MAXN];

struct Node {
    ll value, all, cnt;//在当前区间内再选一头牛的价值，区间总价值，已经拿了几次了
    Node(ll value, ll all, ll cnt) : value(value), all(all), cnt(cnt) {}

    bool operator<(const Node &a) const {
        return value < a.value;
    }
};

ll k, m, n;//草地，敌人牛的数量，自己牛的数量
ll f[MAXN];//敌人的牛的位置
ll p[MAXN << 2], pc;//当前段内关键点，关键点的个数
ll dp[MAXN];
priority_queue<Node> q;

//进行分组
void work() {
    ll all = 0;//当前组内总价值
    ll pi = 1;//下一个还没分配的草地
    //第一头敌人的牛前面的，都可以用一头牛直接拿下
    while (pi <= k && g[pi].p < f[1]) {
        all += g[pi].t;
        pi++;
    }
    q.push(Node(all, all, 0));
    for (int i = 2; i <= m; ++i) {
        //处理f[i-1]到f[i]之间的草
        all = pc = 0;
        ll left = f[i - 1], right = f[i];//左边界，右边界
        ll from = pi;//本组内第1块草
        while (pi <= k && g[pi].p < right) {
            ll ra = min(g[pi].p - left, right - g[pi].p);//当前半径
            g[pi].l = g[pi].p - ra;
            g[pi].r = g[pi].p + ra;
            if (g[pi].l != left) {
                p[pc++] = g[pi].l;
            }
            if (g[pi].r != right) {
                p[pc++] = g[pi].r;
            }
            all += g[pi].t;
            pi++;
        }
        if (from == pi) {
            //这一块内没有草
            continue;
        }
        //对于每个关键点，看看把牛放在关键点左边一点点怎么样
        p[pc++] = right;//右端点也算一个关键点
        sort(p, p + pc);
        ll tt = 0;
        //尺取计算放在每个关键点的答案
        ll tl = from, tr = from - 1, w = 0;
        for (int j = 0; j < pc; ++j) {
            ll pos = p[j];
            while (tr + 1 < pi && pos > g[tr + 1].l) {
                tr++;
                w += g[tr].t;
            }
            while (tl < pi && pos > g[tl].r) {
                w -= g[tl].t;
                tl++;
            }
            tt = max(tt, w);
        }
        q.push(Node(tt, all, 0));
    }
    //最后一个敌人的牛的后面的牛，都可以用一只牛搞定
    all = 0;
    while (pi <= k) {
        all += g[pi].t;
        pi++;
    }
    q.push(Node(all, all, 0));
}

int main() {
    scanf("%lld%lld%lld", &k, &m, &n);
    for (int i = 1; i <= k; ++i) {
        scanf("%lld%lld", &g[i].p, &g[i].t);
    }
    for (int i = 1; i <= m; ++i) {
        scanf("%lld", &f[i]);
    }
    sort(g + 1, g + k + 1);
    sort(f + 1, f + m + 1);
    work();
    ll ans = 0;
    while(n>0 && !q.empty()){
        Node t = q.top();
        q.pop();
        ans+=t.value;
        if(t.cnt==0 && t.value!=t.all){
            t.cnt++;
            t.value = t.all-t.value;
            q.push(t);
        }
        n--;
    }
    printf("%lld\n",ans);
    return 0;
}